D2.2 Determine and compare the theoretical and experimental probabilities of multiple independent events happening and of multiple dependent events happening.
Activity 1: Independent Events
Grade 8 students are looking to determine which team will start with the ball in the next dodgeball game. A student suggests rolling three 4-sided dice to determine the winning team. The team that starts the game with the ball is the one that will get the most points.
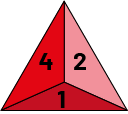
Knowing that Team A has rolled a total of six points, what is the probability that Team B :
- gets more points than the Team A?
- gets less points than the Team A?
- gets the same number of points as Team A?
We are interested in the probability of the combined results when rolling the three dice. The first step is to determine and list the possible equally likely outcomes. If the first die rolled lands on "1", the second die rolled may land on "1", "2", "3" or "4". The same is true for the third die rolled. The same combinations can be represented using a tree diagram:
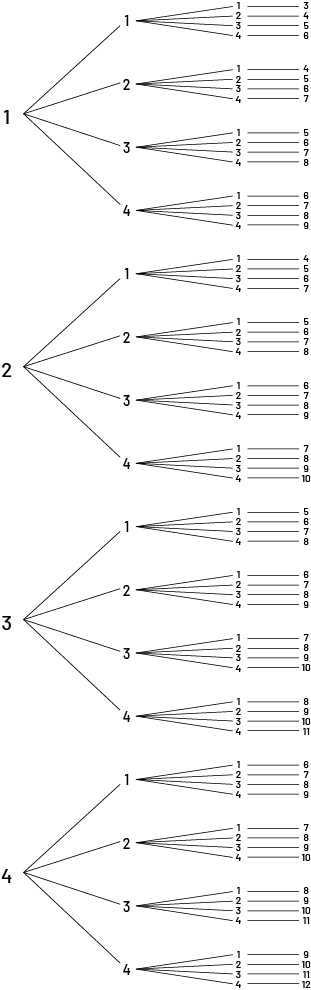image The tree diagram goes like this. The numbers one to four are placed one under the other. From each of them, four branches spread out with the numbers one, two, three, four respectively. From each of them, four more branches unfold, with the numbers one, two, three and four respectively. Each of the scenarios adds up its numbers. One plus one plus one equals three. One plus one plus two equals four. One plus one plus three equals five. One plus one plus four equals six. One plus two plus one equals four. One plus two plus two equals five. One plus two plus three equals six. One plus two plus four equals seven. One plus three plus one equals five. One plus three plus two equals six. One plus three plus three equals seven. One plus three plus four equals eight. One plus four plus one equals six. One plus four plus two equals seven. One plus four plus three equals eight. One plus four plus four equals nine. Two plus one plus one equals four. Two plus one plus two equals five. Two plus one plus three equals six. Two plus one plus four equals seven. Two plus two plus one equals five. Two plus two plus two equals six. Two plus two plus three equals seven. Two plus two plus four equals eight. Two plus three plus one equals six. Two plus three plus two equals seven. Two plus three plus three equals eight. Two plus three plus four equals nine. Two plus four plus one equals seven. Two plus four plus two equals eight. Two plus four plus three equals nine. Deus plus four plus four equals ten. Three plus one plus one equals five. Three plus one plus two equals six. Three plus one plus three equals seven. Three plus one plus four equals eight. Three plus two plus one equals six. Three plus two plus two equals seven. Three plus two plus three equals eight. Three plus two plus four equals nine. Three plus three plus one equals seven. Three plus three plus two equals eight. Three plus three plus three equals nine. Three plus three plus four equals ten. Three plus four plus one equals eight. Three plus four plus two equals nine. Three plus four plus three equals 10. Three plus four plus four equals eleven. Four plus one plus one equals six. Four plus one plus two equals seven. Four plus one plus three equals eight. Four plus one plus four equals nine. Four plus two plus one equals seven. Four plus two plus two equals eight. Four plus two plus three equals nine. Four plus two plus four equals ten. Four plus three plus one equals eight. Four plus three plus two equals nine. Four plus three plus three equals ten. Four plus three plus four equals eleven. Four plus four plus one equals nine. Four plus four plus two equals ten. Four plus four plus three equals eleven. Four plus four plus four equals twelve. Translated with www.DeepL.com/Translator (free version)
Invite students to notice that there are a total of 64 possible outcomes.
Since Team A rolled six points, Team B must get more than six points if it wants to start the next dodgeball game with the ball. By analyzing the tree diagram above, we notice that there are 44 possibilities of getting more than six points. The probability is therefore equal to \(\frac{44}{64}\).
However, there are 10 possibilities of getting less than six points, so the probability that Team B can not start the dodgeball game with the ball is \(\frac{10}{64}\).
The probability that Team B will get the same number of points as Team A is also \(\frac{10}{64}\) since there are 10 possibilities to get six points.
By analyzing the theoretical probabilities, we then notice that it is very likely that Team B will start the game with the ball in the next dodgeball game.
In order to allow for the experimental probability, provide similar equipment to perform the experiment with 100 trials in the classroom. If a 4-sided die is not available, the activity can be done using a 6-sided die.
Activity 2: Dependent Events
Here are the cards available for picking in a card game:
Knowing that the student must draw three cards one after the other without putting them back in the deck, what is the probability that the student will get:
- three aces (AAA)?
- a king followed by two aces?
- a king among the three cards drawn?
To determine the set of possible outcomes, students can use a tree diagram:
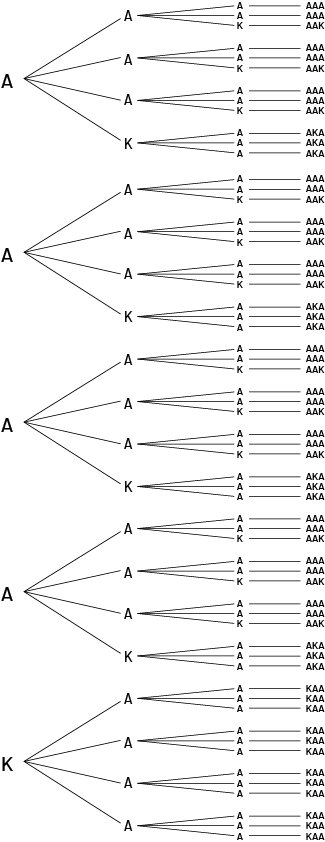image The tree diagram goes like this. Four letters "A" and one letter "K", representing four aces and a king, are placed one below the other. From each of these, four branches unfold with the same letters: A, A, A, K. From each of these, four more branches unfold with the same letters: A, A, A, K. Each of the scenarios creates a set of letters.
From these results, students can determine that the probability of getting:
- three aces equals \(\frac{24}{60}\);
- a king followed by two aces is equal to \(\frac{12}{60}\);
- a king among the three cards is equal to \(\frac{36}{60}\).
In order to allow for the experimental probability, provide similar equipment to perform the experiment with 100 trials in the classroom.