D1.1 identifier des contextes comportant des ensembles de données à une ou deux variables et expliquer dans quels contextes chaque type de données est nécessaire.
HABILETÉ : IDENTIFIER DES CONTEXTES COMPORTANT DES ENSEMBLES DE DONNÉES À UNE OU DEUX VARIABLES
Mise en contexte – une variable
Détermination de ce qui peut être mesuré ou dénombré
Afin de trouver une variable représentée dans un diagramme, on doit déterminer ce qui peut être mesuré ou dénombré.
Exemple
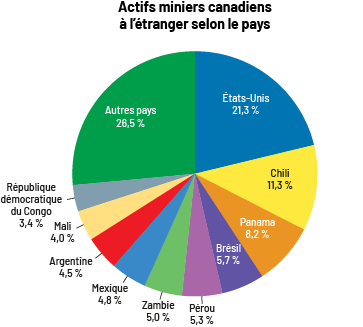 Le diagramme
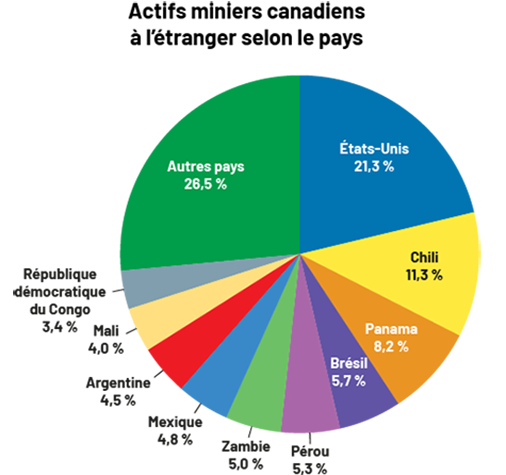
circulaire coloré s’intitule « Actifs miniers canadiens à l’étranger selon le pays ». La partie « Autres pays »
représente 26 virgule 5 pourcent. La partie États-Unis représente 21 virgule trois pourcent. La partie Chili
représente onze virgule trois pourcent. La partie Panama représente huit virgule deux pourcent. La partie Brésil
représente cinq virgule sept pourcent. La partie Pérou représente 5 virgule trois pourcent. La partie Zambie
représente cinq pourcent. La partie Mexique représente quatre virgule huit pourcent. La partie Argentine représente
quatre virgule cinq pourcent. La partie Mali représente quatre pourcent. Et la partie République démocratique du Congo
représente trois virgule quatre pourcent.
Le diagramme
circulaire coloré s’intitule « Actifs miniers canadiens à l’étranger selon le pays ». La partie « Autres pays »
représente 26 virgule 5 pourcent. La partie États-Unis représente 21 virgule trois pourcent. La partie Chili
représente onze virgule trois pourcent. La partie Panama représente huit virgule deux pourcent. La partie Brésil
représente cinq virgule sept pourcent. La partie Pérou représente 5 virgule trois pourcent. La partie Zambie
représente cinq pourcent. La partie Mexique représente quatre virgule huit pourcent. La partie Argentine représente
quatre virgule cinq pourcent. La partie Mali représente quatre pourcent. Et la partie République démocratique du Congo
représente trois virgule quatre pourcent.
Source : Actifs miniers canadiens (rncan.gc.ca).
En observant le diagramme, on remarque que la variable représentée est le pourcentage d’actifs miniers canadiens à l’étranger selon le pays.
Réflexion sur le type de données
Puisque le nombre d’actifs miniers canadiens à l’étranger doit être compté, je sais que ce sont des données quantitatives discrètes.
Mise en contexte – deux variables
Détermination de ce qui peut être mesuré ou dénombré
Afin de trouver les variables représentées dans un diagramme, on doit déterminer ce qui peut être mesuré ou dénombré.
Exemple
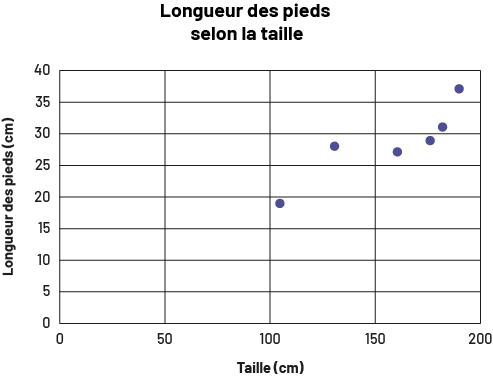 image Le
diagramme à ligne brisée s’intitule « Longueur des pieds selon la taille ». Nommé « Taille en centimètres », l’axe
horizontal est gradué de zéro à 200, tandis que l’axe vertical se nomme « Longueur des pieds en centimètres » et est
gradué de zéro à 40. Le premier point se trouve légèrement après 100 sur l’axe horizontal et légèrement avant 20 sur
l’axe vertical. Le deuxième point se trouve entre 100 et 150, et entre 25 et 30. Le troisième point se trouve entre
150 et 175, et entre 25 et 30. Le quatrième point se trouve entre 150 et 200, et légèrement avant le 30. Le cinquième
point se trouve entre 150 et 200 et légèrement dépassé 30. Et le sixième point se trouve légèrement avant 200 et
légèrement après 35.
image Le
diagramme à ligne brisée s’intitule « Longueur des pieds selon la taille ». Nommé « Taille en centimètres », l’axe
horizontal est gradué de zéro à 200, tandis que l’axe vertical se nomme « Longueur des pieds en centimètres » et est
gradué de zéro à 40. Le premier point se trouve légèrement après 100 sur l’axe horizontal et légèrement avant 20 sur
l’axe vertical. Le deuxième point se trouve entre 100 et 150, et entre 25 et 30. Le troisième point se trouve entre
150 et 175, et entre 25 et 30. Le quatrième point se trouve entre 150 et 200, et légèrement avant le 30. Le cinquième
point se trouve entre 150 et 200 et légèrement dépassé 30. Et le sixième point se trouve légèrement avant 200 et
légèrement après 35.
En observant le diagramme, on remarque qu’il y a deux variables représentées, soit la taille en centimètres et la longueur des pieds en centimètres.
Réflexion sur le type de données
Puisque la taille et la longueur des pieds sont des données qui doivent être mesurées, ce sont des données quantitatives continues.
Source : adapté de En avant, les maths!, 8e année, CM, Données, p. 3-4.
Trouver les variables et le type de données
Exemple 1
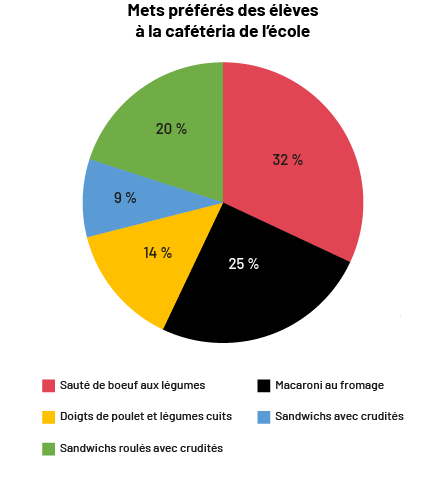 image Le
diagramme circulaire s’intitule « Mets préférés des élèves à la cafétéria de l’école ». Le sauté de boeuf aux légumes
représente 32 pourcent du diagramme. Le macaroni au fromage représente 25 pourcent. Le repas de doigts de poulet et
légumes cuits représente 14 pourcent. Le repas de sandwiches avec crudités représente 9 pourcent. Et le repas de
sandwichs roulés avec crudités représente vingt pourcent.
image Le
diagramme circulaire s’intitule « Mets préférés des élèves à la cafétéria de l’école ». Le sauté de boeuf aux légumes
représente 32 pourcent du diagramme. Le macaroni au fromage représente 25 pourcent. Le repas de doigts de poulet et
légumes cuits représente 14 pourcent. Le repas de sandwiches avec crudités représente 9 pourcent. Et le repas de
sandwichs roulés avec crudités représente vingt pourcent.
Explications :
En observant le diagramme, on peut déterminer qu’il s’agit d’un ensemble de données à une variable. Afin de trouver la variable, on doit chercher ce qui est observé ou mesuré sur les individus d’une population. Dans cette situation, il s’agit du mets préféré des élèves à la cafétéria de l’école.
Nous cherchons aussi à déterminer s’il s’agit de données quantitatives ou qualitatives. Dans cette situation, les noms des divers mets sont des données non numériques donc ce sont des données qualitatives.
La question « Quel est ton mets préféré à la cafétéria de l’école ? » est en lien avec les données. Cette question pourrait permettre, entre autres, au gestionnaire de la cafétéria de retirer ou d’ajouter des mets à son menu afin de mieux répondre aux préférences de sa clientèle.
Exemple 2
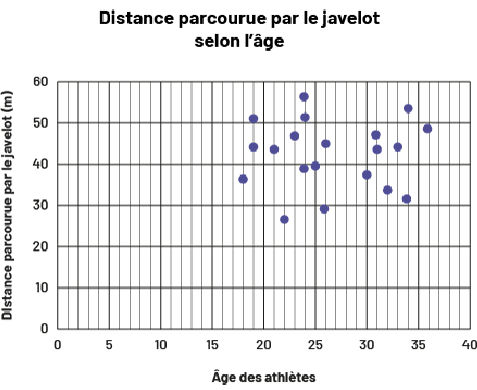 image Le
diagramme de dispersion s’intitule « Distance parcourue par le javelot selon l’âge ». Gradué de zéro à 40, l’axe
horizontal se nomme « Âge des athlètes », tandis que l’axe vertical est gradué de zéro à 60 et se nomme « Distance
parcourue par le javelot en mètres ». Sur l’axe horizontal, le point le plus près de zéro se situe à 19 et le point le
plus loin se situe à 36. Sur l’axe vertical, le point le plus près de zéro se situe entre 25 et 30 (23 ans) et le
point le plus loin se situe entre 50 et 60 (24 ans).
image Le
diagramme de dispersion s’intitule « Distance parcourue par le javelot selon l’âge ». Gradué de zéro à 40, l’axe
horizontal se nomme « Âge des athlètes », tandis que l’axe vertical est gradué de zéro à 60 et se nomme « Distance
parcourue par le javelot en mètres ». Sur l’axe horizontal, le point le plus près de zéro se situe à 19 et le point le
plus loin se situe à 36. Sur l’axe vertical, le point le plus près de zéro se situe entre 25 et 30 (23 ans) et le
point le plus loin se situe entre 50 et 60 (24 ans).
Explications :
En observant le diagramme de dispersion, nous pouvons déterminer qu’il s’agit d’un ensemble de données à deux variables. Afin de trouver les variables, nous cherchons ce qui est observé ou mesuré sur les individus d’une population. Dans cette situation, il s’agit de la distance parcourue par le javelot selon l’âge des athlètes. Ces deux éléments sont donc les variables dans cette situation.
Nous cherchons aussi à déterminer s’il s’agit de données quantitatives ou qualitatives. Dans cette situation, les deux données sont numériques, sont obtenues par comptage et sont placées en intervalles. Ce sont donc des données quantitatives continues.
La question « l’âge a-t-il un effet sur la distance à laquelle l’athlète peut lancer le javelot? » serait en lien avec le contexte et les données. Cette question pourrait être utilisée dans un contexte de préparation sportive par une entraîneuse ou un entraîneur. Celle-ci ou celui-ci pourrait utiliser les données afin de tenter de montrer à ses athlètes que la technique du lancer, et non l’âge, a davantage d’effet sur la distance du lancer puisqu’il n’existe aucune relation entre l’âge des athlètes et la distance parcourue par le javelot selon le diagramme ci-dessus.
HABILETÉ : EXPLIQUER LES CONTEXTES DANS LESQUELS CHAQUE TYPE DE DONNÉES EST NÉCESSAIRE
L’ensemble des données à une variable est utilisé lorsqu’il s’agit de l’observation d’un seul élément au sein d’une population, tandis que l’ensemble des données à deux variables est utilisé lorsque deux éléments au sein de la même population sont observés et comparés.
Exemple
 imageLe
diagramme circulaire coloré s’intitule « Actifs miniers canadiens à l’étranger selon le pays ». La partie « Autres
pays » représente 26 virgule 5 pourcent. La partie États-Unis représente 21 virgule trois pourcent. La partie Chili
représente onze virgule trois pourcent. La partie Panama représente huit virgule deux pourcent. La partie Brésil
représente cinq virgule sept pourcent. La partie Pérou représente 5 virgule trois pourcent. La partie Zambie
représente cinq pourcent. La partie Mexique représente quatre virgule huit pourcent. La partie Argentine représente
quatre virgule cinq pourcent. La partie Mali représente quatre pourcent. Et la partie République démocratique du Congo
représente trois virgule quatre pourcent.
imageLe
diagramme circulaire coloré s’intitule « Actifs miniers canadiens à l’étranger selon le pays ». La partie « Autres
pays » représente 26 virgule 5 pourcent. La partie États-Unis représente 21 virgule trois pourcent. La partie Chili
représente onze virgule trois pourcent. La partie Panama représente huit virgule deux pourcent. La partie Brésil
représente cinq virgule sept pourcent. La partie Pérou représente 5 virgule trois pourcent. La partie Zambie
représente cinq pourcent. La partie Mexique représente quatre virgule huit pourcent. La partie Argentine représente
quatre virgule cinq pourcent. La partie Mali représente quatre pourcent. Et la partie République démocratique du Congo
représente trois virgule quatre pourcent.
Source : Actifs miniers canadiens (rncan.gc.ca).
Ce type de données pourrait, entre autres, être utilisé pour :
- déterminer l’ampleur de la présence mondiale des sociétés canadiennes dans les 10 principaux pays;
- aider les entreprises canadiennes pour savoir où investir dans les prochaines années;
- montrer la répartition géographique des actifs canadiens dans le monde (par exemple, Afrique, Europe, Amérique du Sud, Asie).
Exemple :
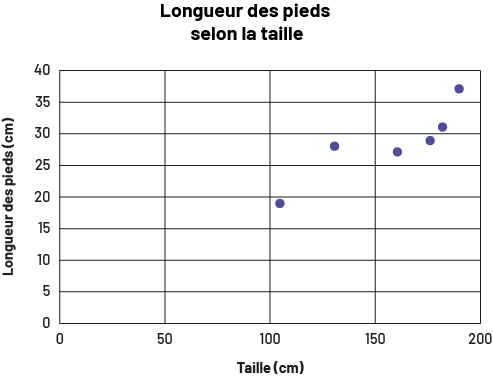 image Le
diagramme à ligne brisée s’intitule « Longueur des pieds selon la taille ». Nommé « Taille en centimètres », l’axe
horizontal est gradué de zéro à 200, tandis que l’axe vertical se nomme « Longueur des pieds en centimètres » et est
gradué de zéro à 40. Le premier point se trouve légèrement après 100 sur l’axe horizontal et légèrement avant 20 sur
l’axe vertical. Le deuxième point se trouve entre 100 et 150, et entre 25 et 30. Le troisième point se trouve entre
150 et 175, et entre 25 et 30. Le quatrième point se trouve entre 150 et 200, et légèrement avant le 30. Le cinquième
point se trouve entre 150 et 200 et légèrement dépassé 30. Et le sixième point se trouve légèrement avant 200 et
légèrement après 35.
image Le
diagramme à ligne brisée s’intitule « Longueur des pieds selon la taille ». Nommé « Taille en centimètres », l’axe
horizontal est gradué de zéro à 200, tandis que l’axe vertical se nomme « Longueur des pieds en centimètres » et est
gradué de zéro à 40. Le premier point se trouve légèrement après 100 sur l’axe horizontal et légèrement avant 20 sur
l’axe vertical. Le deuxième point se trouve entre 100 et 150, et entre 25 et 30. Le troisième point se trouve entre
150 et 175, et entre 25 et 30. Le quatrième point se trouve entre 150 et 200, et légèrement avant le 30. Le cinquième
point se trouve entre 150 et 200 et légèrement dépassé 30. Et le sixième point se trouve légèrement avant 200 et
légèrement après 35.
Ce type de données pourrait être utilisé par des entreprises d’équipement sportif pour :
- déterminer s’il existe un lien entre la taille et la longueur des pieds d’une personne. Si c’est le cas, la commande des souliers pourrait se baser sur celle des vêtements;
- aider des professionnelles et des professionnels de la santé à prédire la taille d’un individu selon la longueur de ses pieds ou vice-versa.
Source : adapté de En avant, les maths!, 8e année, CM, Données, p. 4.
CONNAISSANCE : VARIABLE
Toute quantité ou tout attribut ou nombre qui peut être mesuré ou dénombré.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : ENSEMBLE DE DONNÉES À UNE VARIABLE
Les ensembles de données à une variable font référence à des données qualitatives ou quantitatives. Dans ce contexte, on représente et analyse les données pour répondre à des questions telles que :
- Quelle est la taille moyenne des élèves de la classe?
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : ENSEMBLE DE DONNÉES À DEUX VARIABLES
Les ensembles de données à deux variables font référence à deux ensembles de données du même échantillon ou de la même population. Ces données peuvent être qualitatives ou quantitatives. Dans ce contexte, on représente et analyse les données pour répondre à des questions telles que :
- Y a-t-il une relation entre la taille d’une personne et la longueur de son bras?
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : DONNÉES QUALITATIVES
Données non numériques qui peuvent être organisées en catégories.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : DONNÉES QUANTITATIVES
Données numériques obtenues par comptage ou par mesure.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Les données quantitatives peuvent être discrètes ou continues.
Données discrètes
Données qui peuvent être comptées.
Exemple
Le nombre de billets vendus pour une partie de soccer
Données continues
Données qui peuvent prendre n’importe quelle valeur à l’intérieur d’un intervalle choisi.
Exemple
La vitesse d’une athlète lors d’une course de 200 m; la température de l’eau sur la cuisinière
Source : En avant, les maths!, 7e année, CM, Données, p. 2.
CONNAISSANCE : POPULATION
Ensemble de tous les individus ou objets sur lesquels porte un sondage ou une étude statistique.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : ÉCHANTILLON
Sous-ensemble de la population totale choisi pour faire partie du sondage.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
