D1.3 choisir le type de diagramme le plus approprié pour représenter divers ensembles de données à partir d’une variété de diagrammes, y compris des diagrammes de dispersion; représenter ces données dans des diagrammes comprenant des sources, des titres, des étiquettes et des échelles appropriés; et justifier son choix.
HABILETÉ : CHOISIR LE DIAGRAMME APPROPRIÉ POUR REPRÉSENTER DIVERS ENSEMBLES DE DONNÉES
Visualisation – La représentation des données par des tableaux et des diagrammes permet de communiquer des renseignements en vue de leur interprétation.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 62.
« Il n’existe pas de critères préétablis pour comparer la valeur d’une représentation à celle d’une autre. La valeur relative d’une représentation dépend de l’intention de la question d’intérêt. Les diagrammes ne sont pas meilleurs que les tableaux, les diagrammes à bandes ne sont pas meilleurs que les diagrammes à pictogrammes, etc. Tout dépend du but de l’élève qui crée la représentation. »
(National Council of Teachers of Mathematics, 2003, p. 199, traduction libre)
Comment organiser les données
Divers tableaux et diagrammes sont couramment utilisés en traitement des données pour représenter des ensembles de données avec clarté et pour en faciliter l’analyse. Chacun a ses avantages ainsi que ses limites. Il importe toutefois de noter qu’en général la construction d’un tableau précède la construction d’un diagramme.
Au cycle moyen, selon le contenu d’apprentissage du programme-cadre, les élèves représentent les données à l’aide d’une variété de diagrammes, y compris des diagrammes à bandes multiples, des diagrammes à bandes empilées, des histogrammes et des diagrammes à ligne brisée.
Source adapté : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 66-67.
Au cycle intermédiaire, les élèves pourraient utiliser l’un des modes de représentation enseignés aux niveaux antérieurs. Toutefois, elles et ils peuvent aussi utiliser le diagramme de dispersion, le mode de représentation enseigné en 8e année.
HABILETÉ : REPRÉSENTER DES DONNÉES À L’AIDE DE DIAGRAMMES
Une fois que les données relatives à une enquête ont été regroupées par catégories dans un tableau de fréquences ou autre, il est souvent très utile de les représenter à l’aide d’un diagramme en raison de son aspect visuel.
En effet, un diagramme :
- présente l’information de façon organisée;
- est généralement plus facile à lire et à interpréter qu’une représentation de données à l’aide d’un texte ou d’un tableau;
- permet de voir l’ensemble des données en un coup d’œil et de s’en faire une première impression (par exemple, si les données sont réparties également ou inégalement entre les catégories);
- facilite la prochaine étape du processus d’enquête, soit l’analyse des données et l’interprétation des résultats.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 86.
Les élèves doivent déterminer la meilleure façon de regrouper les données recueillies afin de faciliter leur analyse. Par la suite, elles et ils doivent choisir un mode de représentation approprié et le construire de façon à s’assurer de la clarté du message transmis. Il n’y a pas de règle qui dicte la façon de regrouper les données. Le choix du regroupement dépend en grande partie du type de données recueillies.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 80-81.
L’ordre des catégories est important dans les diagrammes présentant des données quantitatives. Les nombres sont placés en ordre croissant. En revanche, l’ordre des catégories importe peu dans les diagrammes présentant des données qualitatives (par exemple, les couleurs peuvent être placées dans n’importe quel ordre).
Les sources, les titres, les étiquettes et les échelles fournissent des précisions importantes sur les données d’un diagramme.
- La source indique l’origine des données recueillies.
- Le titre présente les données du diagramme.
- Les étiquettes indiquent les catégories ayant servi au classement des données.
- Les échelles indiquent les valeurs sur un axe du diagramme.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
HABILETÉ : JUSTIFIER SON CHOIX DE DIAGRAMME
Afin de pouvoir bien cibler la meilleure représentation pour les données recueillies, les élèves doivent comprendre les caractéristiques et les objectifs des différents types de diagrammes pour choisir la façon la plus appropriée de représenter un ensemble de données. Alors que les données peuvent être visualisées au sein de différents types de représentations, il est important de sélectionner celui qui assure la clarté et la précision des données en contexte. Les élèves sont en mesure de justifier leur choix de diagramme grâce à leurs connaissances approfondies des caractéristiques et des objectifs propres à chaque diagramme.
- Les diagrammes à pictogrammes, les lignes de dénombrement, les diagrammes à bandes, les diagrammes à bandes multiples et les diagrammes à bandes empilées sont utilisés pour présenter des données qualitatives, et des données discrètes.
- Les histogrammes présentent des données continues à l’aide d’intervalles, ainsi que leurs fréquences. Les bandes d’un histogramme n’ont pas d’espace entre elles en raison de la nature continue des données. Cela contraste avec les diagrammes à bandes qui présentent des espaces entre les bandes pour montrer que les catégories sont discrètes.
- Les diagrammes à ligne brisée servent à montrer une évolution dans le temps et sont utiles pour dégager les tendances. Les élèves mettent en pratique leur compréhension des échelles et des estimations pour créer des diagrammes à ligne brisée.
-
Les diagrammes circulaires sont utilisés pour représenter la proportion de chaque catégorie au sein d’un ensemble.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
-
Les diagrammes de dispersion (nuages de points) sont utilisés pour représenter des données à deux variables. On place les valeurs d’une variable sur l’axe horizontal et les valeurs de l’autre variable sur l’axe vertical.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Types de diagrammes comportant une variable
- Diagramme à pictogrammes
- Ligne de dénombrement
- Diagramme à bandes
- Diagramme à bandes multiples
- Diagramme à bandes empilées
- Histogramme
- Diagramme circulaire
Types de diagrammes comportant deux variables
- Diagramme à ligne brisée
- Diagramme de dispersion ou nuage de points
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple : Identification du type de représentation graphique
Pour chacune des séries de données, il est question d’identifier le type de représentation graphique afin de mieux visualiser les liens entre les données.
- L’âge d’une personne a-t-il une incidence sur sa capacité à retenir sa respiration sous l’eau?
| Âge | Durée moyenne sous l'eau |
|---|---|
| 5 ans | 13 secondes |
| 7 ans | 21 secondes |
| 9 ans | 38 secondes |
| 11 ans | 44 secondes |
| 13 ans | 47 secondes |
| 15 ans | 56 secondes |
Source : L'association du souffle
Un diagramme à ligne brisée est de mise, car c’est un diagramme qui sert à illustrer une évolution dans le temps. Dans cette situation, ce sera l’âge en années qui sera représenté sur l’axe horizontal. On doit s’assurer d’inclure les sources, le titre, les étiquettes et d’utiliser des échelles appropriées.
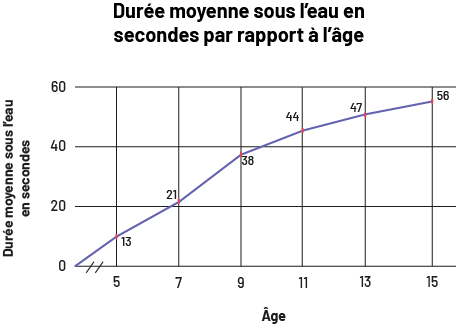image Le
diagramme à ligne brisée s’intitule « Durée moyenne sous l’eau en secondes par rapport à l’âge ». L'axe horizontal se
nomme « Âge » et se gradue de zéro à 16. L’axe vertical se nomme « Durée moyenne sous l’eau en secondes » et se gradue
de zéro à 60. La ligne part de zéro et monte en diagonal. Les points sur l’axe vertical se situent comme suit : 13,
21, 38, 44, 47, 56. Sur l’axe horizontal, la ligne s’arrête à 15.
Source : L'association du souffle
- Quels navigateurs de recherche sont les plus populaires?
- Chrome : 43 %
- Mozilla Firefox : 22 %
- Opera : 16 %
- Microsoft Edge : 11 %
- Vivaldi : 8 %
Puisque les données sont des pourcentages, le diagramme circulaire est le meilleur choix de représentation afin de démontrer chaque partie par rapport à l’ensemble des données. On doit s’assurer d’inclure les sources, le titre, les étiquettes et d’utiliser des échelles appropriées.
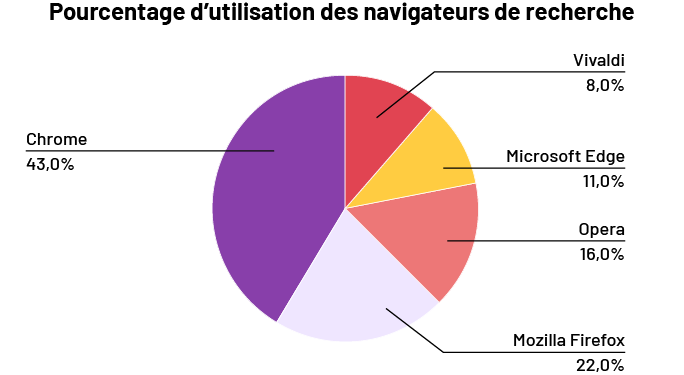image Le
diagramme circulaire illustre le pourcentage d’utilisation des navigateurs de recherche. Il est divisé en cinq
parties. Chrome représente 43 pourcent. Vivaldi représente 12 pourcent. Microsoft Edge représente 11 pourcent. Opera
représente 16 pourcent. Et Mozilla Firefox représente 22 pourcent.
Source : Association des encyclopédies papier du monde
- Quelle est la répartition de groupes d’âge de 15 à 64 ans qui travaillent en Ontario?
| Groupe d'Âge | Pourcentage de la population |
|---|---|
| 15-19 | 9 % |
| 20-24 | 9,9 % |
| 25-29 | 9,7 % |
| 30-34 | 9,6 % |
| 35-39 | 9,4 % |
| 40-44 | 9,7 % |
| 45-49 | 10,4 % |
| 50-54 | 11,8 % |
| 55-59 | 11 % |
| 60-64 | 9,4 % |
Source : Gouvernement de l'Ontario
Un histogramme est à privilégier puisque les données sont continues et organisées en intervalles. La progression de chaque groupe d’âge sera alors bien démontrée. On doit s’assurer d’inclure les sources, le titre, les étiquettes et d’utiliser des échelles appropriées.
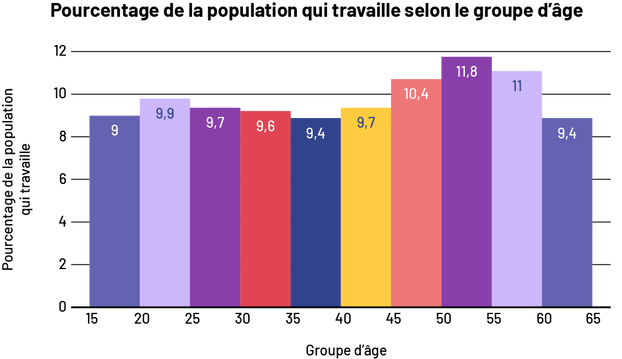image Le
diagramme à bandes s’intitule « Pourcentage de la population qui travaille selon le groupe d’âge ». Gradué de zéro à
60, l’axe horizontal se nomme « Groupe d’âge », tandis que l’axe vertical, gradué de zéro à 12, se nomme « Pourcentage
de la population qui travaille ». De zéro à 15 sur l’axe horizontal, la bande s’élève à neuf sur l’axe vertical. De 15
à 20, la bande s’élève à 9 virgule 9. De 20 à 25, la bande s’élève à 9 virgule 7. De 25 à 30, la bande s’élève à 9
virgule 6. De 30 à 35, la bande s’élève à 9 virgule 4. De 35 à 40, la bande s’élève à 9 virgule 7. De 40 à 45, la
bande s’élève à dix virgule quatre. De 45 à 50, la bande s’élève à onze virgule huit. De 50 à 55, la bande s’élève à
onze. Et de 55 à 60, la bande s’élève à 9 virgule quatre.
Source : Gouvernement de l'Ontario
Source : En avant, les maths!, 8e année, CM, Données, p. 4-7.
CONNAISSANCE : DIAGRAMME
Représentation schématique d’un ensemble de données. Il y a différents types de diagrammes (par exemple, diagramme de Venn, diagramme à bandes, diagramme à bandes multiples, diagramme à bandes empilées, diagramme à ligne brisée, histogramme, diagramme circulaire, diagramme de dispersion).
Note : Un diagramme peut refléter un parti pris s’il n’est pas bien construit.
Exemple
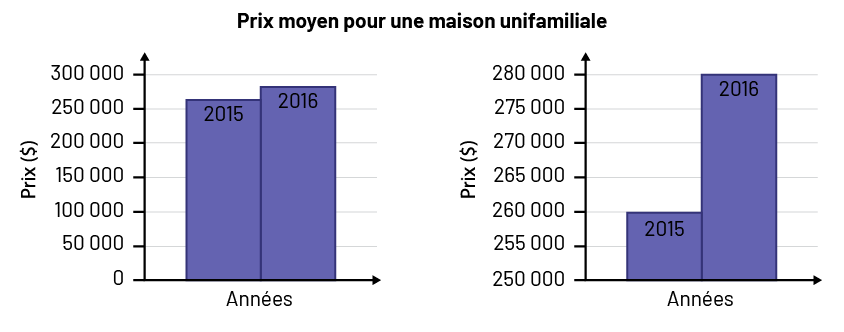image Deux
diagrammes à deux bandes s’intitulent « Prix moyen pour une maison unifamiliale ». Les axes horizontaux des deux
diagrammes se nomment « Années » et les axes verticaux se nomment « Prix en dollars ». Concernant le premier
diagramme, l’axe vertical est gradué de zéro à 300 000. Pour l’année 2015, la bande s’élève légèrement au-dessus de
250 000. Pour l’année 2016, la bande s’élève entre 250 000 et 300 000.Concernant le deuxième diagramme, l’axe vertical
est gradué de 250 000 à 280 000. Pour l’année 2015, la bande s’élève à 260 000. Et pour l’année 2016, la bande s’élève
à 280 000.
Le prix d’une maison a augmenté de 20 000$ en un an. Le premier diagramme montre bien la faible augmentation du prix d’une maison en un an (de 2015 à 2016), puisque l’écart entre les bandes est minime. Le second diagramme est trompeur. Il laisse penser que l’augmentation du prix d’une maison a triplé en un an (de 2015 à 2016), car l’écart entre les bandes est plus grand à cause du choix de l’échelle de l’axe vertical.
Source : En avant, les maths!, 7e année, CM, Données. p. 2-3.
CONNAISSANCE : AXE
Droite utilisée dans un diagramme ou un système de coordonnées. Il y a un axe horizontal et un axe vertical. L’axe horizontal s’appelle l’axe des x (axe des abscisses) et l’axe vertical s’appelle l’axe des y (axe des ordonnées) dans le plan cartésien.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
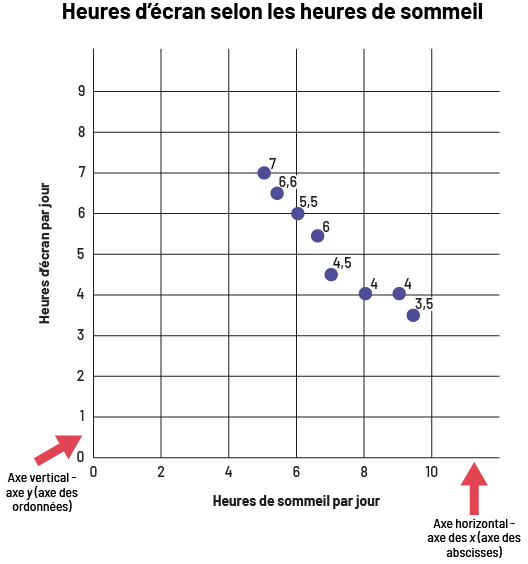image Le
diagramme à ligne brisée s’intitule « Heures d’écran selon les heures de sommeil ». Gradué de zéro à dix, l’axe
horizontal se nomme « Heures de sommel par jour », tandis que l’axe vertical, gradué de zéro à 9, se nomme « Heures
d’écran par jour ». Une flèche rouge pointe l’axe vertical en précisant qu’il se nomme également axe « i grec » ou axe
des ordonnées. Une flèche rouge pointe l’axe horizontal en précisant qu’il se nomme également axe des « x » ou axe des
abscisses.Les points se situent aux endroits suivants. Entre quatre et six sur l’axe horizontal, un point se situe à 7
et l’autre à six virgule six sur l’axe vertical. À six sur l’axe horizontal, le point se situe à cinq virgule cinq sur
l’axe vertical. Entre six et huit sur l’axe horizontal, un point se situe à six et l’autre à quatre virgule cinq. À
huit sur l’axe horizontal, le point se situe à quatre sur l’axe vertical. À 9 sur l’axe horizontal, se point se situe
à quatre sur l’axe vertical. Et entre huit et dix sur l’axe horizontal, le point se trouve à trois virgule cinq sur
l’axe vertical.
Source : En avant, les maths!, 8e année, ML, Données p. 10.
CONNAISSANCE : TITRE
Le titre présente les données du diagramme.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
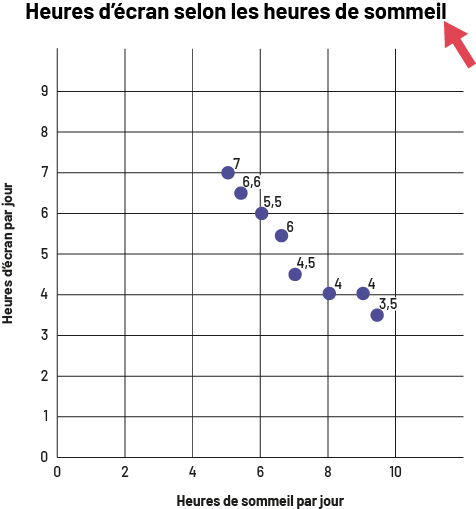
Le diagramme à ligne brisée s’intitule « Heures d’écran selon les heures de sommeil ». Une flèche rouge pointe le titre. Gradué de zéro à dix, l’axe horizontal se nomme « Heures de sommel par jour », tandis que l’axe vertical, gradué de zéro à 9, se nomme « Heures d’écran par jour ».Les points se situent aux endroits suivants. Entre quatre et six sur l’axe horizontal, un point se situe à 7 et l’autre à six virgule six sur l’axe vertical. À six sur l’axe horizontal, le point se situe à cinq virgule cinq sur l’axe vertical. Entre six et huit sur l’axe horizontal, un point se situe à six et l’autre à quatre virgule cinq. À huit sur l’axe horizontal, le point se situe à quatre sur l’axe vertical. À 9 sur l’axe horizontal, se point se situe à quatre sur l’axe vertical. Et entre huit et dix sur l’axe horizontal, le point se trouve à trois virgule cinq sur l’axe vertical.
Source : En avant, les maths!, 8e année, ML, Données p.10.
CONNAISSANCE : VARIABLE
Toute quantité ou tout attribut ou nombre qui peut être mesuré ou dénombré.
Source : En avant, les maths!, 8e année, CM, Données, p. 2.
CONNAISSANCE : ENSEMBLE DE DONNÉES À UNE VARIABLE
Groupe de données interreliées qui font référence à des données qualitatives ou quantitatives.
Source : En avant, les maths!, 8e année, CM, Données, p. 2.
CONNAISSANCE : ENSEMBLE DE DONNÉES À DEUX VARIABLES
Groupe de données interreliées qui font référence à deux ensembles de données du même échantillon ou population.
Source : En avant, les maths!, 8e année, CM, Données, p. 2.
CONNAISSANCE : ÉCHELLE (D’UN DIAGRAMME)
Séquence de nombres associés à des marques qui subdivisent un axe. Une échelle appropriée est choisie pour que toutes les données puissent être représentées dans le diagramme.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
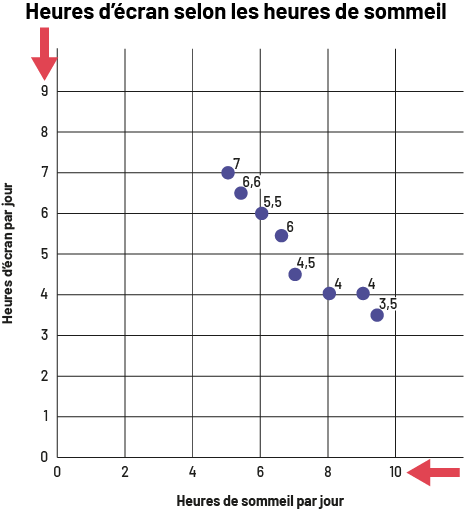image Le
diagramme à ligne brisée s’intitule « Heures d’écran selon les heures de sommeil ». Une flèche rouge pointe le titre.
Gradué de zéro à dix, l’axe horizontal se nomme « Heures de sommel par jour », tandis que l’axe vertical, gradué de
zéro à 9, se nomme « Heures d’écran par jour ». Deux flèches rouges pointent respectivement l’axe vertical et l’axe
horizontal.Les points se situent aux endroits suivants. Entre quatre et six sur l’axe horizontal, un point se situe à
7 et l’autre à six virgule six sur l’axe vertical. À six sur l’axe horizontal, le point se situe à cinq virgule cinq
sur l’axe vertical. Entre six et huit sur l’axe horizontal, un point se situe à six et l’autre à quatre virgule cinq.
À huit sur l’axe horizontal, le point se situe à quatre sur l’axe vertical. À 9 sur l’axe horizontal, se point se
situe à quatre sur l’axe vertical. Et entre huit et dix sur l’axe horizontal, le point se trouve à trois virgule cinq
sur l’axe vertical.
Source : En avant, les maths!, 8e année, ML, Données. p. 10.
CONNAISSANCE : SOURCE
La source indique l’origine des données recueillies du diagramme.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : ÉTIQUETTE
Les étiquettes indiquent les catégories ayant servi au classement des données.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
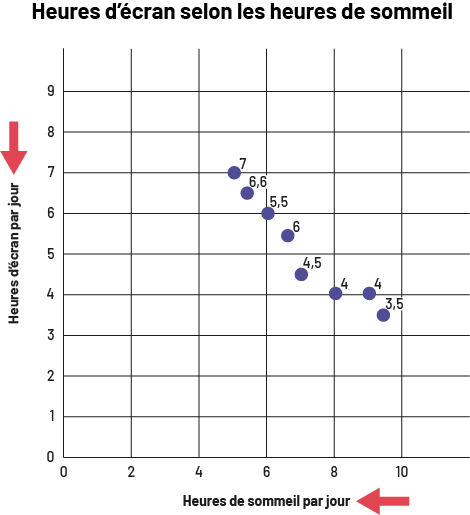image Le
diagramme à ligne brisée s’intitule « Heures d’écran selon les heures de sommeil ». Une flèche rouge pointe le titre.
Gradué de zéro à dix, l’axe horizontal se nomme « Heures de sommel par jour », tandis que l’axe vertical, gradué de
zéro à 9, se nomme « Heures d’écran par jour ». Deux flèches rouges pointent respectivement l’axe vertical et l’axe
horizontal.Les points se situent aux endroits suivants. Entre quatre et six sur l’axe horizontal, un point se situe à
7 et l’autre à six virgule six sur l’axe vertical. À six sur l’axe horizontal, le point se situe à cinq virgule cinq
sur l’axe vertical. Entre six et huit sur l’axe horizontal, un point se situe à six et l’autre à quatre virgule cinq.
À huit sur l’axe horizontal, le point se situe à quatre sur l’axe vertical. À 9 sur l’axe horizontal, se point se
situe à quatre sur l’axe vertical. Et entre huit et dix sur l’axe horizontal, le point se trouve à trois virgule cinq
sur l’axe vertical.
Source : En avant, les maths!, 8e année, ML, Données p. 10.
CONNAISSANCE : DONNÉES DISCRÈTES
Données qui peuvent être comptées.
Exemple : le nombre de sièges dans un avion, le nombre de voitures dans un stationnement ou le nombre de salles de classe dans une école
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : DONNÉES CONTINUES
Données qui peuvent prendre n’importe quelle valeur à l’intérieur d’un intervalle choisi..
Exemple : âge, taille.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : TABLEUR
Logiciel qui permet de créer des représentations graphiques.
Source : En avant, les maths!, 7e année, CM, Donnéess, p. 3.
CONNAISSANCE : TYPES DE DIAGRAMMES (CONNAISSANCES ANTÉRIEURES)
Ligne de dénombrement
Représentation qui permet d’enregistrer rapidement les données d’une enquête à l’intérieur de catégories préalablement désignées en inscrivant un même symbole (par exemple, lettre, crochet) pour chaque donnée dans la colonne appropriée. Ces symboles sont habituellement placés de façon ordonnée afin de faciliter leur dénombrement.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Diagramme à bandes (verticales ou horizontales)
Le diagramme à bandes sert à représenter les fréquences d’un ensemble de données. Il est composé de bandes rectangulaires dont la longueur correspond à la taille des fréquences. Il permet de voir, en un coup d’œil, la distribution des données dans chacune des catégories.
Note : Pour faciliter la construction de diagrammes à bandes, il est recommandé de demander aux élèves d’utiliser du papier quadrillé.
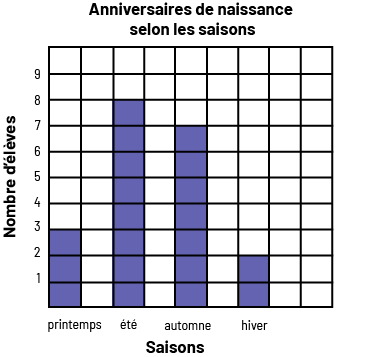
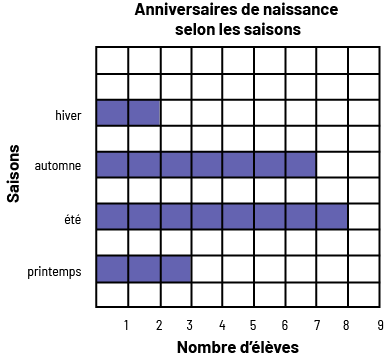
Caractéristiques d’un diagramme à bandes :
- Il a un titre (par exemple, Anniversaires de naissance selon les saisons).
- Il a un axe (vertical ou horizontal) gradué selon une échelle appropriée.
- Il a un autre axe qui représente des catégories (par exemple, printemps, été, automne, hiver).
- Les deux axes ont chacun une étiquette (par exemple, Nombre d’élèves, Saisons).
- Les bandes ont la même largeur et leur longueur correspond, en fonction de l’échelle retenue, à la taille de la fréquence qu’elles représentent (par exemple, si l’échelle est par intervalles de 1, une bande de longueur 3 représente une fréquence de 3).
- Les bandes sont séparées par des espaces égaux.
Source: Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 72.
Diagramme à bandes multiples
Le diagramme à bandes multiples représente plus d’un ensemble de données simultanément. Il a les mêmes caractéristiques qu’un diagramme à bandes, mais chaque catégorie a deux bandes ou plus de données. Une légende indique le code de représentation des données.
Un diagramme à bandes multiples peut être construit selon une orientation horizontale ou verticale. L’orientation choisie dépend d’une préférence personnelle ou de la pertinence de la représentation.
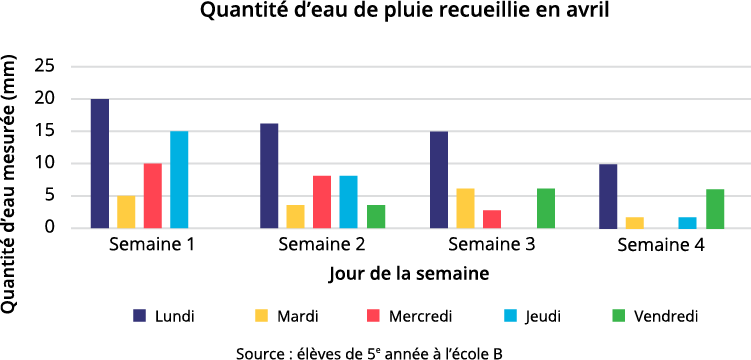image Le titre du
diagramme à bandes multiples verticales est : Quantité d’eau de pluie recueillie en avril.Le titre de l’axe des x est
: Jour de la semaine. L’axe est gradué en quatre semaines, soit semaine 1, semaine 2, semaine 3 et semaine 4.Le titre
de l’axe des y est : Quantité d’eau mesurée (en millimètres). L’axe est gradué par 5, soit de 0 à 25.Il y a une
légende : bleu, c’est lundi, jaune, c’est mardi, rouge, c’est mercredi, bleu pâle, c’est jeudi et vert, c’est
vendredi.Sous la légende, il est écrit « Source : élèves de 5e année de l’école B ».
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Il est possible d’organiser les données de façon à pouvoir comparer plus facilement des catégories de données entre elles. Pour comparer, par exemple, le nombre et le type d’animaux de compagnie des élèves de la 1re à la 6e année, il suffit de résumer les données à l’aide d’un diagramme à bandes multiples, dans ce cas à bandes doubles.
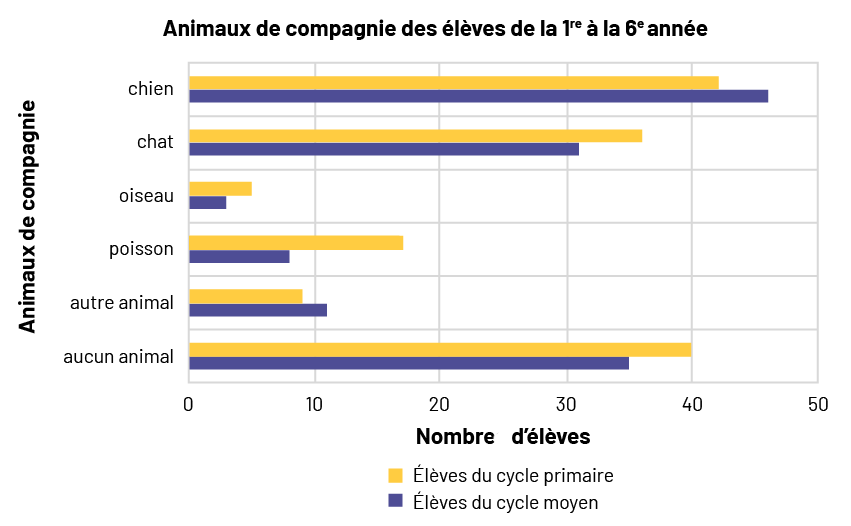image Un diagramme
à bandes doubles horizontales s’intitule « Animaux de compagnie des élèves de la première à la sixième année ». Les
bandes jaunes correspondent aux élèves de la première à la troisième année tandis que les bandes violettes
correspondent aux élèves de la quatrième à la sixième année. Nommé « Nombre d’élèves », l’axe horizontal est gradué de
zéro à 50. L’axe vertical se nomme « Animaux de compagnie ». Pour le chien, la bande horizontale jaune s’arrête entre
40 et 45 tandis que la bande violette dépasse légèrement 45. Pour le chat, la bande jaune dépasse légèrement 35 tandis
que la bande violette dépasse légèrement 30. Pour l’oiseau, la bande jaune atteint cinq tandis que la bande violette
s’arrête avant cinq. Pour le poisson, la bande jaune s’arrête entre 15 et 20 tandis que la bande violette s’arrête
entre cinq et dix. Pour « autre animal », la bande jaune s’arrête un peu avant dix et la bande violette dépasse
légèrement dix. Et pour « aucun animal », la bande jaune atteint 40 tandis que la bande violette atteint 35.
Diagramme à bandes empilées
Les diagrammes à bandes empilées présentent les données de façon proportionnelle. Ces diagrammes peuvent être utilisés pour présenter des pourcentages ou des fréquences relatives. Chaque bande du diagramme représente un tout, et chaque segment d’une bande représente une catégorie différente. Des couleurs différentes sont utilisées dans chaque bande pour différencier les catégories les unes des autres au sein de la même bande. Le diagramme à bandes empilées peut être créé de plus d’une façon pour illustrer différentes comparaisons.
Les bandes empilées sont utiles lorsqu’il y a une deuxième variable nominale dans un ensemble de données, par exemple un ensemble qui comprend les barres granola préférées et l’âge.
Les sources, les titres, les étiquettes et les échelles fournissent des précisions importantes sur les données d’un diagramme :
- La source indique l’origine des données recueillies.
- Le titre présente les données du diagramme.
- Les étiquettes indiquent les catégories ayant servi au classement des données.
- Les échelles indiquent les valeurs sur un axe du diagramme.
- L’échelle des fréquences relatives est indiquée en utilisant des fractions, des décimales ou des pourcentages.
Exemple
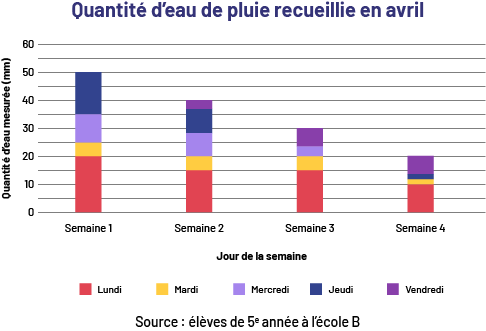image Le
diagramme à bandes empilées s’intitule « Heures d’ensoleillement en juillet ». Sa source provient de l’Association du
souffle. L’axe horizontal correspond à chacune des quatre semaines du mois, tandis que l’axe vertical, gradué de zéro
à 70, correspond aux heures d’ensoleillement. Il y a une couleur pour chaque journée de la semaine : rose pour lundi,
rouge pour mardi, orange pour mercredi, jaune pour jeudi, vert pour samedi, bleu pour samedi et violet pour dimanche.
À la première semaine, la bande s’arrête entre 40 et 45. La journée la plus ensoleillée est le mercredi. À la deuxième
semaine, la bande s’arrête entre 60 et 65. Les journées les plus ensoleillées sont le mercredi, le jeudi et le
dimanche. À la troisième semaine, la bande s’arrête à 45 environ. Les journées les plus ensoleillées sont le mercredi
et le jeudi. Et à la quatrième semaine, la bande s’arrête vers 55. Les journées les plus ensoleillées sont le vendredi
et le dimanche.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Diagramme à ligne brisée
Le diagramme à ligne brisée permet d’illustrer la relation entre deux ensembles de données continues. Des données continues sont des données qui peuvent prendre n’importe quelle valeur à l’intérieur d’un intervalle choisi. Les élèves utilisent habituellement le diagramme à ligne brisée pour illustrer le changement sur une période, tel que le changement de température ou la croissance d’une plante.
Exemple
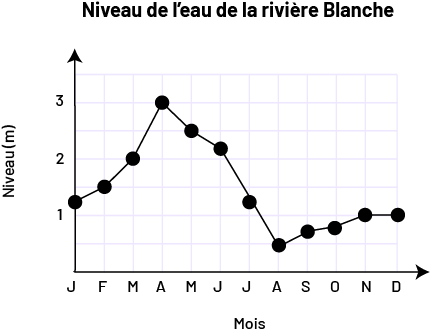image Le
diagramme à ligne brisée à points reliés s’intitule « Niveau de l’eau de la rivière Blanche ». L’axe horizontal se
nomme « Mois » tandis que l’axe vertical, gradué de zéro à trois, se nomme « Niveau en mètres ». À la lettre J, le
point se situe légèrement au-dessus d’un. À la lettre F, le point se situe à un et demi. À la lettre M, le point se
situe à deux. À la lettre A, le point se situe à trois. À la lettre M, le point se situe à deux et demi. À la lettre
J, le point se situe au-dessus de deux. À la lettre J suivante, le point se situe entre un et un et demi. À la lettre
A, le point se situe à un demi. À la lettre S, le point se situe sous le chiffre un. À la lettre O, le point se situe
légèrement plus près du chiffre un. À la lettre N et à la lettre D, le point se situe à un.
Caractéristiques d’un diagramme à ligne brisée :
- Il a un titre (par exemple, Niveau de l’eau de la rivière Blanche).
- Les axes ont chacun une échelle appropriée (par exemple, 0, 1, 2, 3 et J, F, M…).
- Les axes ont chacun une étiquette (par exemple, Mois, Niveau [m])..
- Les données sont représentées par des points.
- Les points consécutifs sont reliés par des segments qui indiquent le changement entre les deux données correspondantes.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 79-80.
Histogramme
Mode de représentation des valeurs prises par une variable continue (par exemple, la taille, l’âge, la masse) sur un échantillon donné. Pour chaque classe, on trace un rectangle dont le côté sur l’axe des abscisses a pour longueur l’amplitude de la classe et dont la hauteur est proportionnelle à la fréquence de la classe. L’histogramme est généralement utilisé pour le traitement de grands ensembles de données. Il n’y a aucun intervalle entre les barres à cause de la nature continue des données. Le graphique formé en reliant les points médians des sommets des colonnes d’un histogramme se nomme le polygone des fréquences.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
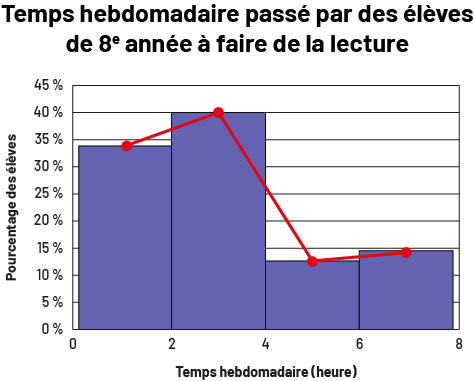image Le
diagramme hybride, à bandes et à ligne brisée, s’intitule « Temps hebdomadaire passé par des élèves de huitième année
à faire de la lecture ». L’axe horizontal, gradué de zéro à huit, se nomme « Temps hebdomadaire en heures », tandis
que l’axe vertical, gradué de zéro pourcent à 45 pourcent, se nomme « Pourcentage des élèves ». Entre zéro et deux, la
bande et le point se trouvent à 34 pourcent. Entre deux et quatre, la bande et le point se trouvent à 40 pourcent.
Entre quatre et six, la bande et le point se trouvent entre dix et 15 pourcent. Et entre six et huit, la bande et le
point se trouvent très légèrement sous 15 pourcent.
Diagramme circulaire
Diagramme illustrant un ensemble de données statistiques dans lequel, pour chaque valeur de la variable, correspond un secteur circulaire dont l’angle est proportionnel à la fréquence de cette valeur.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : DIAGRAMME DE DISPERSION (NUAGE DE POINTS)
On utilise les diagrammes de dispersion (nuages de points) pour représenter des données à deux variables. On place les valeurs d’une variable sur l’axe horizontal et les valeurs de l’autre variable sur l’axe vertical.
Lorsque les points de données sont ordonnés de manière à presque former une droite ou une courbe, cela indique une forte relation (positive ou négative).
Lorsque les points de données sont très dispersés, cela indique une absence de relation.
Les élèves représentent les données par des points dans un diagramme.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemples
Forte relation positive
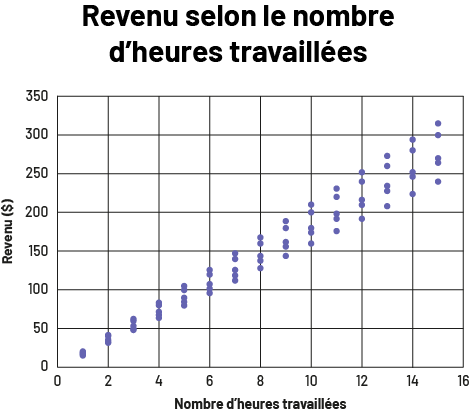image Le
diagramme de dispersion s’intitule « Revenu selon le nombre d’heures travaillées ». Gradué de zéro à 16, l’axe
horizontal se nomme « Nombre d’heures travaillées », tandis que l’axe vertical est gradué de zéro à 350 et se nomme «
Revenu en dollars ». Entre zéro et un, les points sont agglutinés. En progressant dans le diagramme, ils s’alignent
tous à la diagonale, et tendent à s’écarter de plus en plus les uns des autres.
Faible relation négative
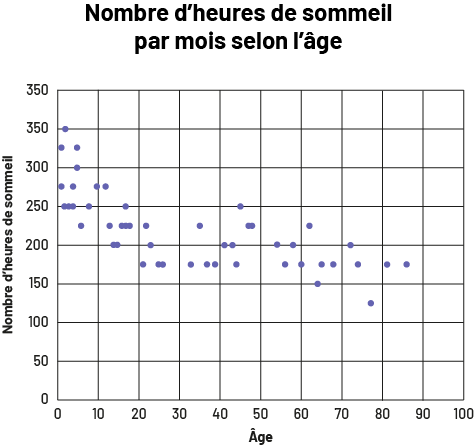image Le
diagramme de dispersion s’intitule « Nombre d’heures de sommeil par mois selon l’âge ». Gradué de zéro à cent, l’axe
horizontal correspond à l’âge, tandis que l’axe vertical est gradué de zéro à 350 et se nomme « Nombre d’heures de
sommeil ». Entre zéro et dix ans, les points se situent entre 225 et 350, puis ont tendance à descendre en avançant en
âge. La tendance remonte un peu entre 35 et 50 ans, puis vers 60 ans. Le point le plus bas se trouve autour de 125,
vers 75 ans.
Absence de relation
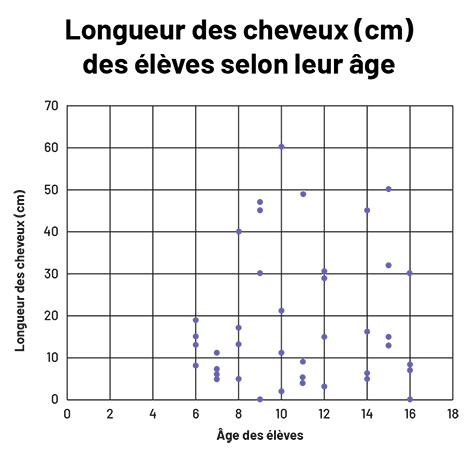image Le
diagramme de dispersion s’intitule « Longueur des cheveux en centimètres des élèves selon leur âge ». L’axe horizontal
se nomme « Âge des élèves » et est gradué de zéro à 18, tandis que l’axe vertical se nomme « Longueur des cheveux en
centimètres » et est gradué de zéro à 70. Le nuage de points est plutôt vaste.