D2.1 résoudre divers problèmes de probabilités, à l’aide d’outils et de stratégies appropriés, y compris des diagrammes de Venn et des diagrammes en arbre.
CONNAISSANCE : PROBLÈME DE PROBABILITÉ
Pour résoudre un problème de probabilité, les élèves doivent s’appuyer sur leurs connaissances antérieures en lien avec la probabilité, faire des prédictions, essayer différentes stratégies, établir des liens et tirer des conclusions.
Source : adapté de Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
Dans un groupe de 10 enfants qui veulent passer du temps ensemble, trois enfants veulent uniquement jouer au soccer, trois veulent uniquement jouer au basketball, deux enfants veulent jouer à l’un ou à l’autre des sports et deux enfants ne veulent pas jouer. Quelle est la probabilité qu’une ou un enfant veule uniquement jouer au basketball?
CONNAISSANCE : DIAGRAMME DE Venn
Le diagramme de Venn est une représentation schématique d’ensembles mettant en évidence leur réunion et leur intersection. Il permet de classer des données selon des caractéristiques communes et de mettre en évidence des relations entre ces données.
Exemple
Lors d’une fête champêtre, on a offert à chaque élève de la classe la possibilité de commander une pointe de pizza, un jus et un dessert.
Voici une partie des données de la commande.
- Niimi a commandé une pointe de pizza, un jus et un dessert.
- Tao a commandé une pointe de pizza et un jus.
- Marek a commandé un jus.
- Jamila n’a rien commandé.
On peut représenter ces données à l’aide d’un diagramme de Venn. Le diagramme comprendra trois cercles, soit un cercle pour chacun des trois choix offerts aux élèves. Voici une façon de représenter les choix de Niimi, de Tao, de Marek et de Jamila.
image Le
diagramme de Venn s’intitule « Choix des élèves ». Les trois ensembles se nomment respectivement comme suit : pointe
de pizza, jus, dessert. Il y a quatre points. Le premier est extérieur au diagramme et vient avec le texte suivant : «
Jamila n’a rien choisi ». Un point se trouve au centre commun des trois ensembles et vient avec le texte suivant : «
Niimi a choisi une pointe de pizza, un jus et un dessert. » Un point se trouve dans l’ensemble partagé entre pointe de
pizza et jus, et vient avec le texte suivant : « Tao a choisi une pointe de pizza et un jus ». Et un point se trouve
dans l’ensemble exclusif au jus, et vient avec le texte suivant : « Marek a choisi seulement un jus ».
Si on représente tous les choix des élèves de la classe, on obtient ce qui suit.
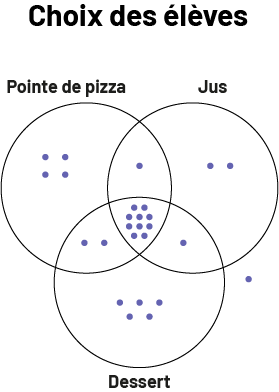image Le
diagramme de Venn s’intitule « Choix des élèves ». Les trois ensembles se nomment respectivement comme suit : pointe
de pizza, jus, dessert.Dans l’ensemble exclusif à la pointe de pizza, il y a quatre points. Dans l’ensemble exclusif
au jus, il y a deux points. Dans l’ensemble exclusif au dessert, il y a cinq points. À l’extérieur du diagramme, il y
a un point. Dans l’ensemble commun aux trois choix, il y a dix points. Dans l’ensemble partagé pointe de pizza et jus,
il y a un point. Dans l’ensemble partagé pointe de pizza et dessert, il y a deux points. Et dans l’ensemble partagé
jus et dessert, il y a cinq points.
On peut ensuite inscrire dans chaque cercle le nombre de points qu’il contient.
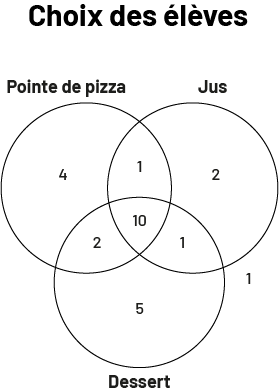image Le
diagramme de Venn s’intitule « Choix des élèves ». Les trois ensembles se nomment respectivement comme suit : pointe
de pizza, jus, dessert.Dans l’ensemble exclusif à la pointe de pizza, il y a le chiffre quatre. Dans l’ensemble
exclusif au jus, il y a le chiffre deux. Dans l’ensemble exclusif au dessert, il y a le chiffre cinq. À l’extérieur du
diagramme, il y a le chiffre un. Dans l’ensemble commun aux trois choix, il y a le nombre dix. Dans l’ensemble partagé
pointe de pizza et jus, il y a le chiffre un. Dans l’ensemble partagé pointe de pizza et dessert, il y a le chiffre
deux. Et dans l’ensemble partagé jus et dessert, il y a le chiffre cinq.
D’après le dernier diagramme, on constate, par exemple, que 10 élèves ont commandé une pointe de pizza, un jus et un dessert, que quatre élèves ont commandé une pointe de pizza seulement et que deux élèves ont commandé une pointe de pizza et un dessert.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 84-86.
CONNAISSANCE : DIAGRAMME EN ARBRE
Le diagramme en arbre sert à dénombrer des éléments de façon à mettre en évidence l’ensemble des choix possibles.
Exemple
Voici une partie d’un diagramme en arbre qui montre les résultats possibles lorsque trois dés sont lancés. Dans cette partie du diagramme, le premier dé lancé est un 1 et le résultat des trois faces des dés sont combinés afin de former un nombre.
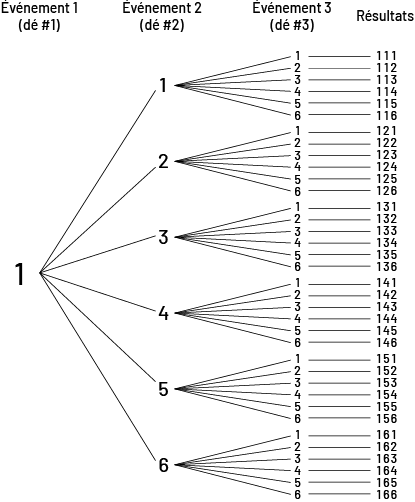image Le
diagramme en arbre élabore tous les scénarios de trois événements. À l’événement un, avec le dé numéro un, il y a le
chiffre un. À l’événement deux, avec le dé numéro deux, il y a les chiffres de un à six, tous reliés à l’événement un.
Et à l’événement trois, avec le dé numéro trois, il y a les chiffres de un à six, tous reliés à chacun des chiffres un
à six de l’événement deux. Cela donne six ensemble de six résultats. Dans le premier ensemble de résultats, les
nombres vont de 111 à 116. Dans le deuxième ensemble, les nombres vont de 121 à 126. Dans le troisième ensemble, les
résultats vont de 131 à 136. Dans le quatrième ensemble, les résultats vont de 141 à 146. Dans le cinquième ensemble,
les résultats vont de 151 à 158. Et dans le sixième ensemble, les résultats vont de 161 à 166.
Source : En avant, les maths!, 8e année, SA, p. 16.