C1. Patterns and Relationships
Identify, describe, extend, create, and make predictions about a variety of patterns, including those found in real-life contexts.
Learning Situation 1: Looking for Patterns
Duration: 2 hours
Contents
In this learning situation, students first examine repeating patterns illustrated on paper strips and then represent them using their bodies. Students then create a strip to decorate the classroom.
| Overall Expectations | Specific Expectations |
|---|---|
| C1. Patterns and Relationships Identify, describe, extend, create, and make predictions about a variety of patterns, including those found in real-life contexts. |
C1.2 Create and translate patterns using movements, sounds, objects, shapes, letters, and numbers. C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in patterns. |
Objective
The purpose of this learning situation is to have students:
- discover a pattern core;
- become familiar with the vocabulary related to patterns.
| Learning Situation | Prior Learning |
|---|---|
| By the time a child enters school, they have a good sense of patterns. In fact, in their daily lives, many actions and gestures are repeated on a regular basis: for example, the sequence of their meals throughout; getting up in the morning, taking a nap in the afternoon, and going to bed at night; putting on their coat, going outside to play, coming back home, and taking off their coat. In preschool, children are encouraged to recognize these patterns and to find others in their environment, such as repeating patterns on wallpaper. When the child spots the pattern, realizes that it repeats, and extends the pattern by explaining their actions, they develop one of the foundations of algebraic reasoning. | To be able to complete this learning situation, students must:
|
Materials
- wallpaper strips with an AB structure (one per team of six and one for set-up) or copies of Appendix MJ.1
- wallpaper strips with a more complex structure
- copies of Appendix MJ.2 (if required)
Mathematical Vocabulary
core, element, term, repeating pattern, order, before, after, next, beside, between
Preparatory Activity
To help students understand what a pattern is, recognize its rule, and extend it, have them create concrete patterns using gestures, sounds or positions. It is desirable to have them first create patterns composed of a simple rule or core; for example, child standing, child sitting, child standing, child sitting, child standing, child sitting. Then, continue with patterns with a more complex rule; for example, child standing, child standing, child sitting, child standing, child sitting, child standing, child sitting.
Before Learning (Warm-Up)
Duration: 45 minutes
Invite students to sit on the floor. Show them a strip of wallpaper (see example below) and ask them if they have wallpaper in their bedroom or elsewhere in the house. If so, invite them to describe it.
Then show them a strip of wallpaper with a simple pattern of two elements that repeat in the same order. If necessary, use Appendix MJ.2 to create strips.
Example

Ask a few students to describe the elements of the pattern on the strip shown; for example, if it is the strip with a sailboat followed by a beach ball, a student might say, "The sails are triangle-shaped and the beach ball is big and round."
Point out the pattern as well as the order in which the elements of the pattern repeat by asking questions such as:
- What is repeated?
- What always comes after the sailboat? after the beach ball?
During the discussion, explain the appropriate terms to students so that they get used to using them.
Examples
- The strip you see is composed of pictures that are always repeated in the same order. It is a pattern.
- Every sailboat and every beach ball you see is part of the pattern. These are the terms of the pattern. Name them with me: sailboat, beach ball, sailboat, beach ball, sailboat, beach ball.
- Each repeating part of the pattern is always composed of a sailboat followed by a beach ball. This part is the core of the pattern.
Expressing the components of the pattern using accurate and precise vocabulary helps students to understand what a pattern is.
Ask the following question: If your body were the sailboat or the beach ball, how might you represent it?
Allow several students to share their ideas. Do not limit them in their choice of suggestions.
For example, students might suggest to:
- make a move;
- take a position;
- produce a sound with the feet or hands.
Choose the suggestions of two students and ask them to come and stand next to the strip to represent with their bodies the first two terms of the pattern.
Example
Tell students, "The two students (name them) become the first two terms in the pattern. They represent the sailboat and the beach ball shown on the wallpaper strip. What do you need to do to extend the pattern?"
Invite all students to come up with an extension of the pattern and explain why they are doing what they are doing, assuming what position, making what sound, etc. To develop algebraic reasoning, it is very important that students justify their choices.
To encourage them to do so, ask them questions such as: How do you know you have to do this?
Examples of possible answers include:
- I am a sailboat because the pattern begins with a sailboat.
- I am a beach ball because it always follows the sailboat.
| Possible Observations | Possible Interventions |
|---|---|
| When students create a pattern with their bodies, they use multiple attributes such as gestures, sounds, and positions in the same pattern. | Do not limit the choice of attributes, but explain that the pattern consists of only two elements and that these two elements (the core) must always be represented in the same way and repeated in the same order to create a pattern. |
| The student does not know what to do to extend the pattern. | Place the student in front of the pattern and ask them to name the terms in the pattern: sailboat, beach ball, sailboat, beach ball, sailboat, beach ball. Ask them to name the term that they must represent. Point out the gesture made, the sound produced, or the position taken by the other students who represent this term. Explain that they must represent the term in the same way in order to maintain the repetition of the pattern core. |
| The student chooses a different gesture, sound, or position than the one that represents the term; for example, the student makes a triangle with their arms outstretched in front of them rather than overhead to represent the sailboat. | Point out to the student that the sailboats on the strip are always the same and that the students representing them must do the same thing so that the pattern core repeats. |
| The student cannot justify their choice of element to extend the pattern. | Place the student in front of the pattern and ask them to name the terms in the pattern:
sailboat, beach ball, sailboat, beach ball, sailboat, beach
ball until their turn. Ask them questions such as:
Ask another student to help them formulate a rationale and have the student repeat the rationale. Use Appendix MJ.2 to create another strip with a two-element pattern; for example, fire truck and firefighter, drum and guitar. These elements could be represented by sounds and follow the same process as before. |
Active Learning (Exploration)
Duration: 20 minutes
Form teams of six and give each team a different pattern core with two repeating elements, that is, a pattern with an AB structure (use Appendix MJ.1 or MJ.2). Ask the teams to represent this pattern with their bodies; for example, standing and crouching; knee slapping and finger snapping; jumping and pivoting. Encourage the use of different attributes in creating the patterns (gesture, sound, position, etc.) so that the mathematical sharing is richer.
Circulate and observe the strategies used by each team. Intervene, if necessary, by asking questions such as:
- What part of the pattern are you representing?
- Describe how the pattern repeats.
- Why do you stand in this spot in the pattern?
- What is the next element in the pattern? How do you know?
- Why do you say that this is the first part of the core? the last?
- What happens next in the pattern?
- How might you represent this pattern with different gestures? different sounds? different positions?
Teams should consist of at least six students, as it is important to present the entire pattern at least three times before recognizing it or extending the pattern core. This makes it easier for students to identify the relationship between the elements and patterns. In addition, developing the ability to work as a team is a very important learning in the Primary Division.
Note: Depending on the needs of the class, this activity may be done differently from the one above; for example, teachers may work with one group of six students at a time in an activity centre. While waiting for their turn, the others can create patterns with two repeating elements using concrete materials. If students are having difficulty grasping the concept, encourage them to do the activity more than once.
Consolidation of Learning
Duration: 45 minutes
Ask students to come and sit on the floor in the meeting area.
Ask each team to take turns presenting their pattern on a strip of paper, and representing it with sounds or movements, and giving explanations and justifications. Ask the other students to name the elements of the core in the pattern.
Ask questions of the presenting team to draw out appropriate concepts and vocabulary.
Examples
- What is the name of the repeating part?
- What are the elements of the pattern?
- What is the repeating pattern?
- What comes next in the pattern?
Continue by comparing two patterns constructed with different attributes. Point out, with the help of questions, that the parts of the core in the two patterns are repeated in the same order.
Examples of similarities and differences observed by students
- There is always one element followed by a different element in both pattern cores.
- There are two elements in the core of the two patterns.
- The core is always repeated in both patterns.
- One of the patterns is built with sounds and the other with positions. The attributes are different.
When students realize that patterns represented with different attributes have the same rule (an AB structure), they take a step forward in their algebraic reasoning.
Extension 1: More Complex Patterns
This activity helps students consolidate their understanding of patterns. Present them with a more complex pattern to represent; for example, a pattern with an ABC core, such as the one shown below. Ask students to identify the pattern, name the elements that make up the pattern, and explain how they might represent the pattern with their bodies.
Example

Divide the class into two teams and give a pattern with this core to nine students in a team. Ask them to represent this pattern with their bodies, using gestures, sounds or positions as attributes. Ask the other students to add to the pattern in a way that extends it and to justify their choice of gestures, sounds, or positions.
Ask students to find similarities and differences between an AB pattern (patterns constructed during exploration) and an ABC pattern using the following points:
- attributes;
- number of elements in the pattern;
- repetition of the pattern;
- order of the pattern elements.
Extension 2: Creation of Wallpaper Strips
This activity helps students deepen their understanding of the various components of a pattern.
Group students into pairs. Provide them with several copies of different illustrations or several stampers. Ask them to create a pattern on a strip of paper and exchange it with another team.
Then ask them to represent the resulting pattern using attributes such as gestures, sounds, or positions, and then describe the repeating pattern core.
Display the illustrated patterns on strips of paper to decorate the classroom.
Creating a pattern requires more complex algebraic reasoning than recognizing an existing pattern and extending it.
The activity helps to verify important aspects of algebraic reasoning:
- understanding the structure of the pattern (the pattern is simple or complex);
- understanding of regularity (the pattern core repeats itself);
- the ability to represent and establish links between the elements in a pattern;
- the ability to generalize (state the pattern rule).
Differentiated Instruction
The learning task can be modified to meet the different needs of the students.
| To Facilitate the Task | To Enrich the Task |
|---|---|
|
Ask students to name their attribute as they move to give verbal clues that will support them in determining the rule more easily. Reproduce several patterns with the same rule before creating different patterns. |
Make the pattern more complex by adding an element to the pattern or changing the order; for example, clap, jump, snap, rotate, an ABCD structure. |
Follow-Up at Home
At home, students can:
- create a pattern of positions, gestures, or sounds, and then ask a family member to determine the repeating pattern;
- determine the repeating pattern core in a pattern that a family member has created;
- discuss with a family member activities that are repeated, such as getting up in the morning and going to bed at night, every day;
- find a strip of wallpaper or a decorative object with a repeating pattern, or draw a pattern core on a strip of cash register paper and bring it to school. Back in the classroom, students present their pattern by describing it and explaining the repeating pattern.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 73-82.
Learning Situation 2: Necklace Detectives
Duration: 2 hours
Summary
In this learning situation, students create a repeating pattern by making a bead necklace and comparing the patterns of the necklaces. Then, students play detective to discover the bead that was removed from their partner's necklace. Strategies used to find the missing bead are discussed.
| Overall Expectations | Specific Expectations |
|---|---|
| C1. Patterns and Relationships Identify, describe, extend, create, and make predictions about a variety of patterns, including those found in real-life contexts. |
C1.1 Identify and describe the regularities in a variety of patterns, including patterns found in real-life contexts. C1.2 Create and translate patterns using movements, sounds, objects, shapes, letters, and numbers. C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in patterns. |
Objective
The purpose of this learning situation is to have students:
- analyze the relationships between elements in a pattern;
- determine the rule;
- find the missing element.
| Learning Situation | Prior Learning |
|---|---|
By exploring repeating patterns, Grade 1 students develop basic concepts related to patterning. Students
begin by discovering that regularity is created when pattern cores repeat and that they can extend a pattern
by adding elements. In Grade 1, most students can find the rule in patterns with a simple structure such as
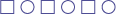 (AB structure) and can extend it
fairly easily. However, students usually have more difficulty finding the missing elements in a pattern, since
this skill requires analysis of relationships; for example, finding the missing element in the pattern core (AB structure) and can extend it
fairly easily. However, students usually have more difficulty finding the missing elements in a pattern, since
this skill requires analysis of relationships; for example, finding the missing element in the pattern core
 . In order to make the rule more
obvious, it is important to repeat the core of a pattern at least three times before asking students to find
any missing element. . In order to make the rule more
obvious, it is important to repeat the core of a pattern at least three times before asking students to find
any missing element.
|
To be able to complete this learning situation, students must be able to:
|
Materials
- beads of different colours and sizes
- long shoelaces (one per student)
- resealable plastic bags (one per student, optional)
- plastic sewing needles and wool in different colours (optional)
Mathematical Vocabulary
non-numeric pattern, element, position, missing element, repeating pattern, order
Before Learning (Warm-Up)
Approximate Duration: 30 minutes
Explain to the students that they will be taking part in a fundraiser to improve the schoolyard. Students will be selling beaded necklaces that they have made.
Present to the class a necklace with a red bead followed by two blue beads (ABB structure).
Don't Forget!
It is best if the necklace has at least three repetitions of the pattern core so that students can identify the regularity.
Ask students the following question: How would you describe the necklace to someone who would like to buy one, but can't see it?
By asking them questions, have students discuss:
- attributes of the pattern, such as colour or shape;
- elements of the pattern; for example, red bead, blue bead, blue bead; round bead, square bead, square bead;
- the core of the pattern; for example a red bead followed by two blue beads;
- the number of elements of each kind in the pattern core; for example, one red and two blue beads;
- the order of the beads according to the attribute in the pattern; for example, red, blue, blue; round, square, square;
- regularity in the pattern core (the elements of the pattern are always repeated in the same order).
Encourage students to describe the pattern using appropriate mathematical vocabulary (for example, attribute, element, position, pattern, core).
In Grade 1, it is best to use the term repeating pattern to name the regularity, since this creates an image of the pattern in the students' minds.
Group students into pairs. Provide them with beads. Ask them to create a repeating pattern that is an example of their necklace. Explain that each member of the team must create a different pattern.
Suggestions: Prepare one bag of beads per team. Give them two shoelaces with a knot at one end to prevent the beads from falling off. Have students work sitting on the floor to prevent the beads from falling off the desks.
Circulate among the teams and observe the strategies used. Provide support as necessary, by asking students questions such as:
- What is the core of the pattern?
- What is repeated?
- How does the pattern repeat?
- Can you show me the elements of your design?
- What attribute did you use to create your pattern?
Once the necklace has been made, ask students to show it to their partner. Explain that each member of the team must explain, using appropriate mathematical vocabulary, the pattern represented by their partner's necklace. Then ask them to find similarities and differences between the necklaces.
Examples of patterns that have the same attribute, but a different structure

Attribute: shape
Structure: ABB

Attribute: shape
Structure: AAAB

Attribute: colour
Structure: ABB

Attribute: colour
Structure: ABC
Choose a few students whose patterns have different structures and ask them to present their necklace to the others and explain its structure.
Ask other students if they have created a necklace that has a similar structure to any of the structures presented. Group the necklaces that have the same structure and point out the similarities and differences.
Then choose a student whose necklace has a different and more complex structure than the patterns presented. Discuss the similarities and differences.
Save the necklaces for the next step.
| Possible Observations | Possible Teacher Moves |
|---|---|
| The student creates a necklace without a repeating pattern. |
Ask the student to name each element in their pattern core aloud while touching each named bead. Ask the student if anything was repeated as they named them. Explain to the student that in order for there to be a pattern, the elements of their pattern must repeat. Remove the beads from the lace without undoing the order to make it easier to move them. Ask the student to name the bead that begins the pattern. Tell the student that, in order for there to be a pattern, each pattern must begin with this shape or colour of bead. Ask the student to name the bead that comes after the first one. Tell them that this colour or shape of bead must always follow the first in the pattern. Continue this for each bead in the pattern. Have the beads placed in such a way as to form the pattern three times, moving them without stringing them on the lace. Have the student name this new pattern by touching each bead, then name the elements of the repeating pattern. |
| The student creates a pattern and names the elements starting from the right while moving to the left. | Explain to the student that the description of the elements is from left to right, just like in reading. This way, everyone understands the same thing. |
| The student leaves a space between each pattern core. | Have the student eliminate the spaces to help their partner analyse the beads and find the repeating pattern. |
Active Learning (Exploration)
Approximate Duration: 30 minutes
Explain to students that when you put your necklace away (the necklace from the warm-up), it broke, and when you put the beads back on the lace you noticed one was missing. Leave a space representing the missing bead and show them the necklace.

Tell students that the space that represents the lost bead is a missing element in the bead pattern and that they will play detective to find it.
Choose a detective and ask them to identify the missing bead in the necklace. Place the bead suggested by the student by the space and ask them to justify their choice.
Note: It is very important that the student justifies their choice. The identification of the missing element is done by establishing the relationship with the other elements. The ability to justify one's choice contributes to the development of algebraic reasoning.
Ask the other students if they found the missing term in another way.
Point out the strategies used to find the missing element; for example,
- some students will recognize a rule: "The red bead is always followed by two blue beads, so the missing element is a blue bead;
- others will first recognize the pattern core (red bead, blue bead, blue bead) and use it to find the missing element.
Form teams of two. Give each student the necklace they made during the warm-up. Explain that they are going to play detective.
First, ask them to remove a bead from their necklace. Specify that they can remove the bead from the beginning, middle, or end of the necklace. Then, the partner must find where the bead is missing. On the first few tries, make sure students leave a space where the bead was to make it easier.
If some teams finish the activity before others, ask them to extend their partner's necklace.
Circulate among the students and observe their work. Select three necklaces for the math exchange: one with the bead removed at the beginning of the necklace, one in the middle, and one at the end.
Consolidation of Learning
Approximate Duration: 30 minutes
Ask students to come and sit on the floor in the meeting area.
Have a student who has removed a bead (the missing element) from the middle of their necklace present it to the others. Ask them questions such as:
- Where is a pearl missing?
- Can you explain how you discovered the missing pearl?
- Does any other student have a missing bead in the middle of their necklace?
- Did your partner discover your missing pearl in another way?
Show students, through discussion or demonstration, that the repeating pattern of the necklace helps discover the missing element.
Continue in this way to determine the missing bead in different places on the necklaces. Point out the strategies used to find it.
Examples
Student says, "They removed a red cube because in the other parts of the necklace there is always a red cube after the green sphere." They recognized two attributes (shape and colour) and used the bead before it as a strategy to discover the missing element.

Student says, "They removed an orange bead because the pattern core is orange, orange, green." They checked the core of the two subsequent patterns.

The student says, "In the middle there is a red bead missing because at the beginning it is red and green, and at the end it is green and red, so in the middle the pattern has to be red and green like the others. If it was green that was missing, there would be two others at the end too because the pattern repeats itself. Here it would be red, green, green, green, red, green, green, green." They check the repeating pattern as well as the validity of their result by eliminating the possibility that it is the other colour that is missing.

A student says, "It's the yellow bead that's missing at the end of the necklace because at the beginning of the necklace it's always blue, blue, yellow, but the yellow colour is missing at the end of the last pattern core." The student determines the rule of the pattern from the beginning of the necklace.

Ask students if it is easier to find the missing bead when it is at the beginning, middle, or end of the necklace. Also ask if it is different when the necklace pattern is more complex. Listen to their justifications.
To enrich the exchange, invite students to redo the activity by removing the space that indicates the location of the missing bead. Then ask them to continue by removing two consecutive beads instead of one. Point out that they must always justify their answer.
Extension: Measuring to Pack
Ask students to create a box in which to place the necklace (and bracelet, if applicable) to protect it for sale. This activity is an interesting extension for students who wish to take on other challenges. It also promotes the integration of concepts from the Spatial Sense strand. The shape of the box and its dimensions can become a rich problem-solving situation.
Differentiated Instruction
The learning situation can be modified to meet the different needs of Grade 1 students.
| To facilitate the task | To enrich the task |
|---|---|
Ask students:
|
Ask students:
|
Follow-up at Home
Students can take their necklace home and describe the rule to a family member. Students can also look for objects that have the same rule; for example, wallpaper, tiles on a floor, patterns on clothing, artwork. Students can also reproduce them on a sheet of paper or take a picture of them to display in the "Museum of Regularities" at school and then discuss them.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 97-107.
