General Foundations of Algebra
Primary Division
Algebra is the mathematical field that arose from the need to understand and organize the real world, for example, the movement of stars, what light is, the shape of the Earth. Mathematicians have tried to answer these questions through observation and the invention of new calculation techniques.
Several authors (Driscoll, 1999; Squalli, 2002) have raised the importance of making connections between arithmetic and algebra. Arithmetic is generally understood as computational work with known quantities that focuses on efficiency in finding the right answer. However, algebra involves analysing the patterns of relationships among quantities in order to generalize mathematical ideas and identify mathematical structures. For this reason, it is important to develop analytical thinking (reasoning) skills in elementary school by laying the foundation for algebraic thinking.
Take, for example, 2 + 3 = 3 + 2. Arithmetically, students can think about this by adding each side of the equal sign to confirm that both sides equal 5. Algebraically, they can think about the fact that when two numbers are added, the order in which they are added does not matter, and the sum will be same, i.e., the commutative property of addition.
The study of patterns is also part of the study of algebra; it is a more concrete way to get students to observe both change and order in the world around them. This introduces students to the observation of change and the analysis of relationships in those changes, as change is an important component of algebraic thinking.
Algebraic Thinking
In the search for a definition of what algebraic thinking is, many prioritize a perspective that is considered essential in algebra.
The development of algebraic thinking involves several interacting factors, namely:
- fundamental processes to access higher levels of abstraction (abstracting, generalizing and operating on variables);
- mathematical skills developed from an algebraic perspective (problem solving, reasoning and communication);
- components of the learning environment (understanding relationships, representing with symbols, using models, and analyzing change);
- algebraic concepts grouped according to the big ideas (patterns and relationships, and expressions and equality).
The image below illustrates the interaction between these factors.
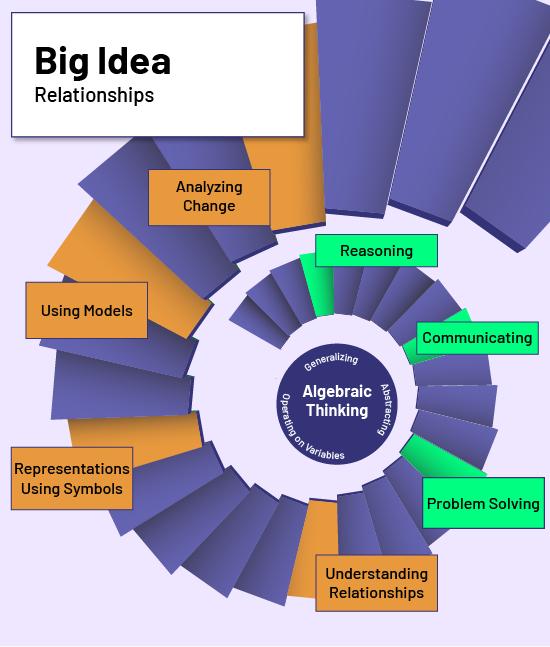 image Infographics: Big ideas. Patterns and relationships. Expressions and equality. A descending spiral staircase with the following words spiraling down with the staircase. Analyze change, Use models, Represent with symbols, Understand relationships, Solve a problem, Communicate, Reason. At the bottom of the spiral staircase is a circle with the following words inside: Algebraic Thinking, Generalize, Abstract, Operate on a variable.
image Infographics: Big ideas. Patterns and relationships. Expressions and equality. A descending spiral staircase with the following words spiraling down with the staircase. Analyze change, Use models, Represent with symbols, Understand relationships, Solve a problem, Communicate, Reason. At the bottom of the spiral staircase is a circle with the following words inside: Algebraic Thinking, Generalize, Abstract, Operate on a variable.
Algebraic Concepts Grouped According to Two Big Ideas
Grouping various algebraic concepts into big ideas is an important factor in the development of algebraic thinking.
To help teachers define and prioritize key concepts and implement strategies that provide effective and coherent instruction, two big ideas are presented, explored, and developed in the Algebra strand. While interrelated, these two big ideas each have a particular emphasis. They allow students to explore relationships in patterns and to understand equivalent relationships.
| BIG IDEA 1: Patterns and Relationships | BIG IDEA 2: Expressions and Equality |
|---|---|
| Exploring regularities in patterns supports an understanding of the relationships that exist between various objects and numbers as well as between numbers themselves. | The concept of equality is essential for establishing relationships represented by objects, numbers or symbols. Equality refers to the relationship between two quantities or expressions that have the same value. |
| Key point 1 Exploring non-numerical patterns allows students to recognize and describe the regularity and relationships that exist between the terms. |
Key point 1 Numerical expressions are equivalent when they produce the same result. |
| Key point 2 Exploring numerical patterns allows students to recognize and describe the regularity and relationships that exist between the terms. |
Key point 2 The equal sign represents equality between two expressions. |
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 5-7, and p. 27.
Developing algebraic thinking is a complex journey that relies on three fundamental processes: abstracting, generalizing, and operating on variables.
Abstracting
Abstracting involves detaching oneself from the sensory aspect of things in order to reason at a more general level (adapted from Raynal and Rieunier, 2003, p. 13), that is, to mentally represent a concrete situation. Piaget considers abstraction to be one of the major processes that allow the construction of knowledge. For his part, Roegiers (2000, p. 77) explains that the appropriation of a concept generalizes reality (for example, a regularity that does not exist in reality, but which is observed in a pattern). The concept is thus situated on another plane than reality. This is the domain of abstraction.
Generalizing
Generalizing involves drawing valid conclusions, true in all cases, from the observation and analysis of a few examples (adapted from Squalli, 2002, p. 9). Generalization is at the heart of mathematical activity. Generalizing '...is particularly important because in humans it is the basis for the acquisition of concepts and the ability to abstract' (Raynal & Rieunier, 2003, p. 156).
In situations of equality, students can more easily formulate a generalization when it follows a process of proposing and verifying a conjecture.
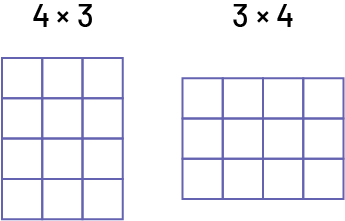
In algebra, students can more easily generalize when making conjectures. In the Primary Division, the properties of numbers and operations are one of the subjects of conjectures. For example, when students assume that changing the order of the terms in a multiplication has no effect on the product, this is a conjecture.
Example 1
Example 2
When students see a recursive phenomenon as they explore various equality situations, they can propose a conjecture. For example, students might say that if the number 0 is added to any number, the initial quantity does not change. Students should then check whether their conjecture is valid in other similar situations. For example, in the situation in the previous example, students could check it with various numbers as well as with concrete materials. When a conjecture seems to apply to all similar situations, students make a generalization with words or symbols.
Example 3
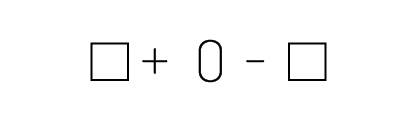
In the Primary and Junior Divisions, conjectures are usually expressed in words by students. They may also be represented by concrete or semi-concrete materials to illustrate their mathematical reasoning.
Teachers should expose students to a variety of problem-solving situations that challenge them to practice making and testing conjectures; for example, the teacher could present the number sentence 50 + 6 − 6 = 50 and then offer the following conjecture: 'I wonder, when you add and subtract the same number in a number sentence, if it is the same as adding or subtracting zero.' Teachers then invite students to discuss this conjecture with each other and determine if it is always true.
Students test this conjecture with other number sentences. They may not be convinced that it applies to any number sentence or to all numbers, especially large numbers. In the course of the discussion, they can propose their own conjectures as illustrated below.
 picture Two students discuss: Student One: The number sentence 100 plus 5 minus 5 equals 100 is true because if you subtract a number from itself, it is the same as if you had not added it. The sentence then becomes 100 equals 100. Student 2: I believe the number sentence is true because subtracting a number from itself is the same as adding a zero. The starting quantity does not change. So the sentence would become 100 plus zero equals 100.
picture Two students discuss: Student One: The number sentence 100 plus 5 minus 5 equals 100 is true because if you subtract a number from itself, it is the same as if you had not added it. The sentence then becomes 100 equals 100. Student 2: I believe the number sentence is true because subtracting a number from itself is the same as adding a zero. The starting quantity does not change. So the sentence would become 100 plus zero equals 100.
After a check of various number sentences, students conclude that the conjecture is true and formulate a generalization.
Example 4

Since students' vocabulary in elementary school is not fully developed and precise, initial conjectures usually need to be rephrased or clarified. Ideally, therefore, the formulation of a conjecture should be practiced in a class setting, as shown in the example below. During the discussion, students can point out the limitations of a peer's conjecture and contribute to the formulation of a clearer and more relevant conjecture. However, it is important for teachers to establish a learning environment in which students perceive each other's questions as positive interactions that can fuel the discussion.
Example 5
The teacher presents the number sentence 564 + 0 = 564 and asks students if it is true or false.
- Student: 'It is true.'
- Teacher: 'How can you tell?'
- Student: 'When a zero is added to a number, it doesn't actually add anything. Therefore, we get the starting number.'
The teacher presents other similar number sentences. After several such discussions, the teacher then asks students to formulate a conjecture.
- Student: 'All numbers added with a zero remain the same.'
- Another student presents a counterexample: 'No, because (100 + 300 = 400). The numbers 100 and 300 have zeros in them. When added together, they do not remain the same.'
After further discussion, a student formulates another conjecture:
- Student: “When you join a zero to another number, you get the other number. »
- Other student: 'That's not true.'
- Teacher: So, are you referring to the number that is right next to a zero?
- Student: No, added to another number.
After much discussion, the following formulation is adopted: Zero, added to another number, is equal to that number. When students see that this conjecture applies to all numbers, they can generalize.
Operating on Variables
Operating on variables involves reasoning, thinking about operations, and making generalizations (adapted from Squalli & Theis, 2005). Research suggests that this is what distinguishes arithmetic from algebra (Squalli, 2002; Driscoll, 1999). The variable is usually represented by a letter. However, in many situations, it can be represented by a symbol or concrete material, or it can be expressed verbally.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 111.
Through the Algebra strand, students' thought processes will evolve so that they begin to solve problems,, to reason, and to communicate algebraically.
Ability to Solve a Problem Algebraically
A problem situation refers to a problem that:
- is open-ended;
- is broad;
- can be solved in teams;
- is put into context;
- is a challenge for everyone;
- promotes the use of different strategies.
From grades 1 to 3, problem solving is designed to engage students in a process that requires the use of different strategies. Students who have developed strategies find it easier to initiate the resolution of a problem, to anticipate and predict outcomes, to reason and to find a solution.
One of the goals of problem solving in algebra is to acquire intellectual tools for reasoning (for example, looking for regularities, establishing relationships, using different representations). Problem solving from an algebraic perspective involves using models to attempt a solution.
In the primary grades, students have few models to draw on. Teachers need to introduce and use them explicitly to help students make them their own. Models may appear to be more numerical in nature, but using them from an algebraic perspective will develop algebraic thinking.
For example, teachers introduce students to the use of an open double number line to get them to think about the calculation, not do the calculation. The important thing is to understand the equality relationship, namely, 9 + 6 = 8 + 7. It is not to calculate, for example, the sum of 9 + 6 or 8 + 7.
Example
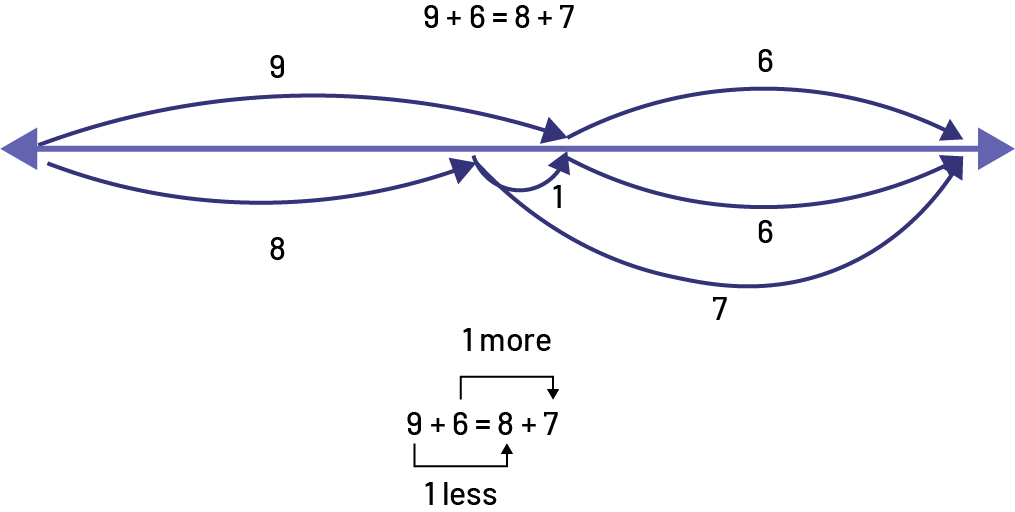
Gradually, students adopt models, integrate them into their strategies and use them spontaneously to solve a problem. A problem-solving situation that is contextualized and challenging arouses interest and motivates students to develop a solution. It involves a process that requires anticipation, drawing on previous experience, and sense-making, which promotes the development of algebraic thinking.
Ability to Reason Algebraically
Algebraic reasoning is about observing and acting differently depending on what one does in arithmetic, and using a set of analytical thought processes, such as generalizing, operating on unknowns, and expressing relationships.
The table below shows the main distinction between reasoning arithmetically and reasoning algebraically.
 image The table below shows the main distinction between arithmetic and algebraic reasoning. In numeracy, we look for the unknown value by remembering a basic numerical fact. 14 equals 7 plus triangle. The student may think: 7 plus question mark, equals 14. 14 minus 7 equals question mark. The double of 7 is 14, so the unknown value is 14. In algebra, we look for relationships between numerical expressions and analyze the numbers. We can find the unknown value without performing any operations. 8 plus 6 equals 7 plus triangle. Eight is one more than 7. The value of the triangle is 7, because one more than 6 is 7. Important: 8 plus 6 equals 7 plus triangle. In the bubble: 8 is one more than 7. The value of the triangle is 7, because one more than 6 is 7. At first, to explore these relationships, it is essential to use concrete materials and models, such as the open double number line.
image The table below shows the main distinction between arithmetic and algebraic reasoning. In numeracy, we look for the unknown value by remembering a basic numerical fact. 14 equals 7 plus triangle. The student may think: 7 plus question mark, equals 14. 14 minus 7 equals question mark. The double of 7 is 14, so the unknown value is 14. In algebra, we look for relationships between numerical expressions and analyze the numbers. We can find the unknown value without performing any operations. 8 plus 6 equals 7 plus triangle. Eight is one more than 7. The value of the triangle is 7, because one more than 6 is 7. Important: 8 plus 6 equals 7 plus triangle. In the bubble: 8 is one more than 7. The value of the triangle is 7, because one more than 6 is 7. At first, to explore these relationships, it is essential to use concrete materials and models, such as the open double number line.
Source: translated and adapted from L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Through algebraic reasoning, students analyze patterns and relationships between numbers, symbols, quantities, and operations in order to generalize them.
The intellectual process required for algebraic reasoning is not a simple and natural one. Teachers should engage students in this process:
- by helping them to make their thinking visible;
- encouraging them to work backwards, that is, to reverse the process, from the answer to get to the starting point;
- by encouraging them to find patterns and organize information to represent the situation in a different way and to generalize;
- by having them observe the relationships between numbers or operations;
- by allowing them to demonstrate their approach.
In order to teach students to articulate their thinking, teachers should ask questions that emphasize algebraic concepts and that lead them to reflect.
Examples include:
- Does it work if I do the same with other numbers?
- What changes?
- What does not change?
- Can I predict the outcome based on the information gathered?
- Does the rule work in all cases?
- Do I always follow the same steps? What are they?
Ability to Communicate Algebraically
The ability to communicate algebraically, both orally and in writing, is developed through sharing understandings. When students discuss their understanding of a situation or concept, it is done through two distinct elements: modes of representation and the use of mathematical arguments.
Modes of Representation
To communicate effectively, students can use different modes of representation. Mathematical relationships can be represented using concrete or semi-concrete materials, symbols, or verbal descriptions.
When representing an algebraic situation using one or two modes of representation, students use a variety of models such as tables, number grids, or number lines.
These models help them organize, record, and communicate their thinking as they explore relationships. The representation of a situational problem using concrete, visual (semi-concrete) or symbolic models, along with a verbal description, facilitates the observation of relationships and contributes to the development of algebraic thinking. The different representations allow students to internalize algebraic concepts.
A significant mathematical step in the development of algebraic thinking is to understand that two patterns can be constructed with different material but have the same rule or that an equality can be represented using different models.
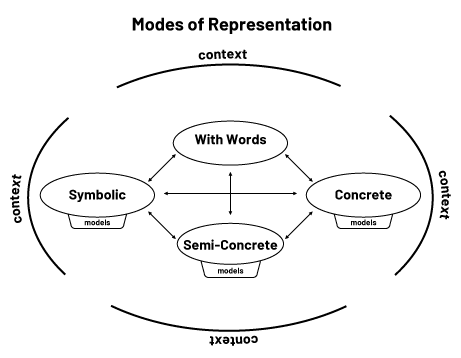
Use of Mathematical Arguments
A mathematical argument is an oral or written justification of a reasoning in order to demonstrate or refute a mathematical idea.
Exchanging mathematical ideas gives students the opportunity to share and deepen their understanding and promotes the development of algebraic thinking.
By taking ownership of an algebra problem, students suggest conjectures, present possible solutions, compare their ideas or justify their results using different representations.
Note: In the Primary Division, students may have difficulty developing a clear conjecture. The teacher must, through the relevance of their questioning, take advantage of mathematical conversations with the whole class to encourage the formulation of conjectures.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 15.
A learning environment conducive to the development of algebraic thinking should incorporate the following four components: understanding patterns and relationships, representing problem situations using symbols, using mathematical models to represent relationships between quantities, and analyzing change. Each of these components is discussed below.
Understanding Patterns and Relationships
Recognizing regularities is an important problem-solving skill; it allows for the internalization of other concepts and the formulation of conjectures leading to generalizations. The concept of regularity is the cornerstone of algebraic reasoning.
By observing and analyzing the relationships between numbers within a pattern, within a number sentence, or within the base ten system, students discover patterns and can deepen their understanding of algebraic concepts.
From an early age, children become aware of regularities in the world around them (for example, the arrangement of ceramic tiles in the bathroom, the cycle of day and night, routines of the day).
In the early grades, algebraic reasoning can be developed through the exploration of patterns, presented in a variety of forms using various attributes such as movements, sound, color, geometric shapes, and numbers.
For example, the story Goldilocks and the Three Bears is an interesting tool to introduce students to the concepts of patterns and regularity, and to establish relationships between the terms in a pattern. Throughout the story, students discover that the pattern is always made up of three 'big, medium, small' elements that repeat in the same order. This is a good opportunity to introduce them to patterns and relationships.
Recognizing, comparing, representing, describing, extending, and creating patterns in the context of problem solving leads students to establish relationships between the terms of a pattern.
Representation of Problem-solving Situations Using Symbols
Representing and analyzing problem situations is a fundamental component of algebraic thinking. To be successful in algebra, one must be able to use symbolic representations of real or contextualized situations. Real situations represented initially with concrete or semi-concrete material will gradually be represented by symbols. In order to build a solid foundation for understanding algebraic concepts, it is important to move students gradually toward a more formal symbolic representation. The use of symbols facilitates the achievement of a higher level of abstraction, especially when representing regularities or numbers in situations of equality.
In Algebra, students need to understand the meaning of symbols. This involves:
- understanding the value of symbols;
- knowing how to make judicious and relevant use of them;
- representing a context by symbols.
Some people draw a parallel between number sense and the meaning of symbols. Among others, Arcavi (1994) conceives of symbol meaning as a spontaneous and accurate appreciation or instinctive understanding of the symbol.
He states that the meaning of the symbol is manifested by the following actions:
- demonstrating relationships, generalizations and even justifications that would otherwise be difficult to grasp;
- choosing a possible symbolic representation to represent and solve a problem;
- determining whether the situation requires a symbolic representation or another representation;
- manipulating the symbols, reading them and visualizing the results and possible regularities.
As early as the primary grades, students demonstrate an understanding of the properties of mathematical operations such as the commutativity of addition with specific objects or numbers. Students use concrete materials, drawings, words, or symbols to represent mathematical ideas and relationships, including the equality relationship. Students describe and represent quantities in a variety of ways, and improve their ability to use symbols to communicate their ideas.
Later, students become aware of the meaning of symbols (for example, squares, circles, letters) to express unknown quantities, and then also learn to use them to express relationships by writing equations.

The presentation of authentic problems promotes the understanding of the concept of unknown quantities while helping to demystify the use of symbols.
Example 1
A farmer has three pens: one for horses, one for cows and one for sheep. The three pens are connected by paths, as shown below. The numbers in the picture show the total number of animals in two pens connected by a path. How many animals can be in each pen?
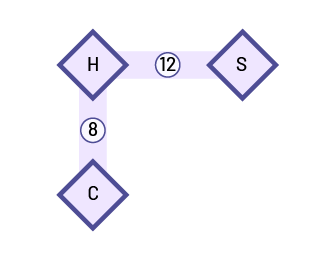
Using small plastic animals, students determine the possible quantities of animals in each pasture. For example, a student might place four cows (4c), four horses (4h) and eight sheep (8s) in the respective pastures. Then, to justify their reasoning, the student writes a number sentence that corresponds with their representation.
Example 2:
4 h + 4 c = 8 animals
4 h + 8 s = 12 animals
The use of manipulatives provides a concrete way to see the possible relationships between variables. In the primary grades, this strategy focuses on understanding rather than on the abstract use of symbols. It develops reasoning and algebraic thinking.
The ability to manipulate symbols allows students to analyze a problem, choose an appropriate representation, select an effective strategy for solving it, and evaluate whether their solution is plausible.
Use of Mathematical Models to Represent Relationships Between Quantities
Mathematical models are used to study relationships. Over time, mathematicians have created, used, and generalized certain ideas, strategies, and representations to make concepts easier to grasp. Through use, certain representations have become accepted models, for example, the number line and the ten-frame. It is important that students use mathematical models in a variety of activities to understand relationships between quantities.
Faced with a problem to be solved, several representations are possible; some students use their bodies, manipulatives or drawings, while others represent the data more schematically. The way in which the data are represented and organized reflects the level of development of algebraic thinking. The models explored in the Primary and Junior Divisions will differ depending on the level of abstraction of the students. A variety of models can be used to solve a problem. In this resource, the word model refers to the various concrete, semi-concrete, and symbolic representations of the problem, but it also refers to how each student uses personal symbols to represent their reasoning.
Examples of Models
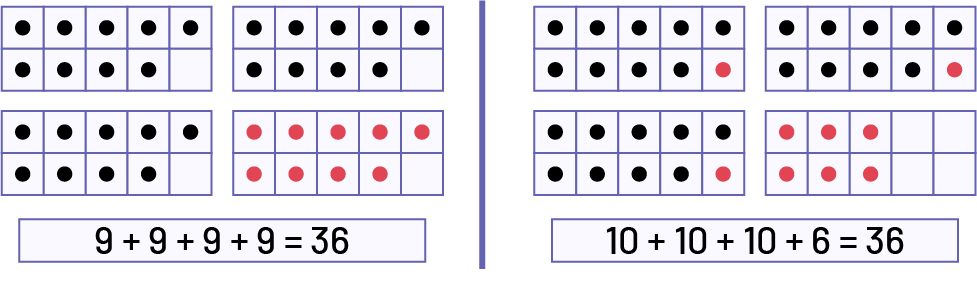
Problem 1: A grocer bought 4 cases of lemons. In each case, there are 9 lemons. How many lemons did he buy altogether?
The Ten Frame
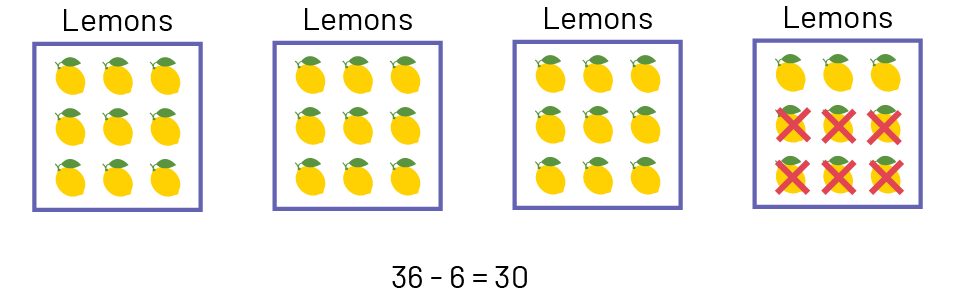
Problem 2: If he sells 6, how many lemons will he have left?
The Array
The Number Line

Problem 3: How many lemons will he have if he buys 5 cases? 6 cases? 7 cases?....
Table of Values
| Number of Cases | Number of Lemons |
|---|---|
| 1 | 9 |
| 2 | 18 |
| 3 | 27 |
| 4 | 36 |
| 5 | 45 |
| 6 | 54 |
| 7 | 63 |
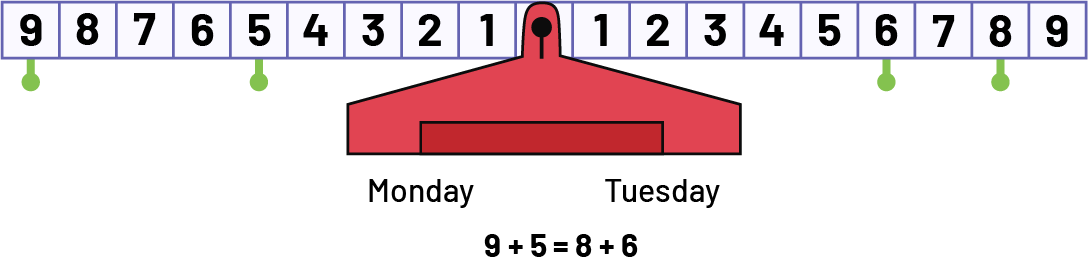
Problem 4: On Monday, the grocer sold 9 lemons to one customer and 5 to another. On Tuesday, he sold 8 to Mr. Lauzon and 6 to Mrs. Qureshi. He says he sold the same number of lemons on Monday and Tuesday. Is this true or false?
To solve this problem, students can use the open double number line, the pan balance, or the math scale.
The Double Open Number Line
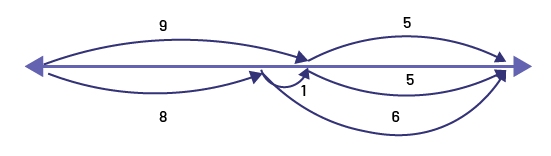
This is true because
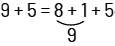
The Pan Balance

The Mathematical Balance
Teachers should introduce these models to students as they support the development of algebraic reasoning. In representing a problem, students can analyze relationships using these models, draw conclusions, and explain their reasoning using verbal descriptions. Models are tools that help students formalize their algebraic thinking.
Models are primarily representations for exploring changes, illustrating relationships, and proposing conjectures in a variety of contexts in order to gain ownership of concepts. Fosnot and Dolk (2001, p. 77) describe them as mental maps used by mathematicians to organize and solve problems and to explore relationships.
Just as they do with symbols, students use models to make sense of the relationships between numbers and operations. By allowing them to analyze problems in a more abstract way, models facilitate understanding. And at the heart of these models, students have access to the meaning of number, the concept of relationships between numbers, and ultimately, the development of fundamental processes.
According to Fosnot and Dolk (2001), models, like big ideas and strategies, cannot be transmitted automatically; students must construct them themselves in order to internalize them. It is therefore important to present them with problems that are conducive to modelling, so that students create their own symbols and models to represent situations, instead of systematically proposing the usual algorithms or learned strategies.
Thus, as students progress through school, they should use strategies initially explored through these models, treating them as valuable tools. Through this transfer, common and familiar mathematical relationships will be used to support less common situations presented in new contexts.
Note: Many algebra activities can be seen as number activities; in fact, it is mainly the algebraic orientation provided by the teacher that will allow students to enter the world of algebra.
Understanding Change
Students live in a changing world. Understanding that change is a part of life and that most things change over time (for example, each year their height and weight increases and their feet grow in length) is an important aspect of algebraic thinking. Observed changes can be described qualitatively (for example, I am taller than last year; my hair is longer; the bucket filled with water quickly during the storm; it is colder now than this morning) and quantitatively (for example, I grew 2 cm this year; the bucket of water filled with 50 mL in 30 minutes; the temperature dropped 6°C in 3 hours). Students need to learn to observe and understand changes in patterns and in situations of equality.
For example, to maintain equality in a given situation, students must understand and demonstrate how the change in one variable affects the change in the other variable. For example, in an exploratory situation where students are asked to find all possible combinations of two rods that, when placed end-to-end, are the same length as the reference rod, they quickly realize that changing one rod requires changing another rod.
When students understand this relationship, rods are no longer changed randomly, but are chosen more systematically, demonstrating the emergence of algebraic thinking. Understanding that most things undergo change, that these changes can be described mathematically, and that some of them can be predicted, is an important part of developing algebraic thinking.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 16-22.
Teachers are vital in the development of algebraic thinking in the primary classroom. The teacher's role is not defined solely by the choice of tasks, but also by their teaching moves, which aim to encourage students to go beyond arithmetic reasoning and to access a symbolic way of thinking. Doing mathematics thus takes on its full meaning.
Some authors (for example, Blanton & Kaput, 2003, pp. 70-77) believe that teachers need 'algebraic eyes and ears' to identify and maximize connections to algebraic concepts in mathematical activities and to take advantage of opportunities to develop students' algebraic thinking.
To do this, the teacher can:
Vary the parameters of a problem
Use an existing problem and give it an algebraic perspective, by promoting the search for relationships, patterns, conjectures and generalizations.
For example, consider the following problem typically associated with the Numbers strand:
In a team of four people, how many handshakes will there be if each person shakes hands with all the other people only once?
The teacher could use this problem and ask questions that draw out connections to algebraic concepts, such as:
- How many handshakes will there be if one, two or three other people are added to the team?
- Organize the data in a table of values. Do you see a pattern?
- How many handshakes will there be if ten people are added to the team?
Ask questions to help students generalize
- What can be said about the relationship between the number of people on the team and the total number of handshakes?
- Is there a regularity? Explain your answer.
Ask questions with an emphasis on algebraic concepts
- Can you explain the problem in your own words?
- Can you solve the problem using another representation?
- How do we make sure that this solution is true?
- Would this approach work with other numbers? Always?
- What changes?
- What does not change?
These questions encourage students to make conjectures and explain them with mathematical arguments.
Develop and strengthen symbol literacy
Teachers should understand that symbol literacy is an important concept for students and to support them in its development. Too often, the application of mathematical symbols is done automatically, with students perceiving these symbols simply as a command to perform a mathematical operation. Students can then have difficulty solving problems correctly and explaining the meaning of the number sentences they have written because they do not understand the symbols used. The teacher should be mindful of supporting students to:
- read the symbols and think about what they represent before acting;
- understand the correct meaning of mathematical symbols (for example, the '=' sign represents a relationship between the numerical expressions on either side of the sign and is not a precursor to the answer);
- recognize and use symbols as communication tools to interpret a mathematical sentence and to express reasoning.
Creating an 'algebraic' learning environment
An 'algebraic' learning environment is one where the development of analytical thinking is emphasized. Teachers consciously identify times when reasoning is an integral part of their instruction. Arguing, abstracting, and generalizing become common practice during daily lessons in mathematics and even in other subjects, not an occasional enrichment.
Creating an 'algebraic' learning environment means giving students the chance to experience the world around them with 'algebraic' eyes and ears, able to generalize explicitly.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 23.
