C2. Equations and Inequalities
Demonstrate an understanding of variables, expressions, equalities, and inequalities, and apply this understanding in various contexts.
Learning Situation: What a Nice Surprise!
Duration: 125 minutes
Contents
In this learning situation, students represent the contents of two goody bags using visual (semi-concrete) materials, words, and symbols. They then write a number sentence to represent the quantities of objects in these bags and check if it is true.
Note: This activity is best introduced when students begin to symbolically represent concrete addition situations with number sentences.
| Overall Expectations | Specific Expectations |
|---|---|
| C2. Equations and Inequalities Demonstrate an understanding of variables, expressions, equalities, and inequalities, and apply this understanding in various contexts. |
C2.2 Determine whether given pairs of addition and subtraction expressions are equivalent or not. C2.3 Identify and use equivalent relationships for whole numbers up to 50, in various contexts. |
Objective
The purpose of this learning situation is to have students:
- represent equivalent relationships in different ways;
- make a connection between different representations of quantities and the corresponding number sentences.
| Learning Situation | Prior Learning |
|---|---|
| Understanding the concept of equivalence is essential to the development of algebraic reasoning. Therefore,
students need to experience a variety of situations in which they will practice recognizing, defining,
creating, and establishing an equivalence.
It is important to help them to understand that the symbol for equality, the = sign, which reads "is equal to", means that the numbers or expressions on either side of the = sign represent the same quantity. Using students' prior knowledge, teachers should encourage students to explore different representations of the same equality situation. |
To be able to complete this learning situation, students must be able to:
|
Materials
- two goody bags containing 10 elements each (the first bag containing three different types of elements and the second containing two different types of elements)
- large sheets of paper (one per student)
- 10 frames (two per student)
Mathematical Vocabulary
equality situation, as much as, is equal to, is not equal to, equal quantities, equality symbol, = sign, number sentence
Before Learning (Warm-Up)
Duration: approximately 50 minutes
Introduce the situation to students by saying:
I found two goody bags at home. I wrote the letter A on the first bag and the letter B on the second. Let's see what's in each bag.
Place bags A and B in front of the students. Ask a student to take out the objects in bag A and describe them. Ask another student to do the same with bag B. Use this opportunity to introduce new words to the students, such as kaleidoscope and spinning top.).
Ask students the following question:
- How could you arrange the elements in each goody bag to compare the number of elements of each kind?" (By grouping identical elements together, as shown in the photos below).
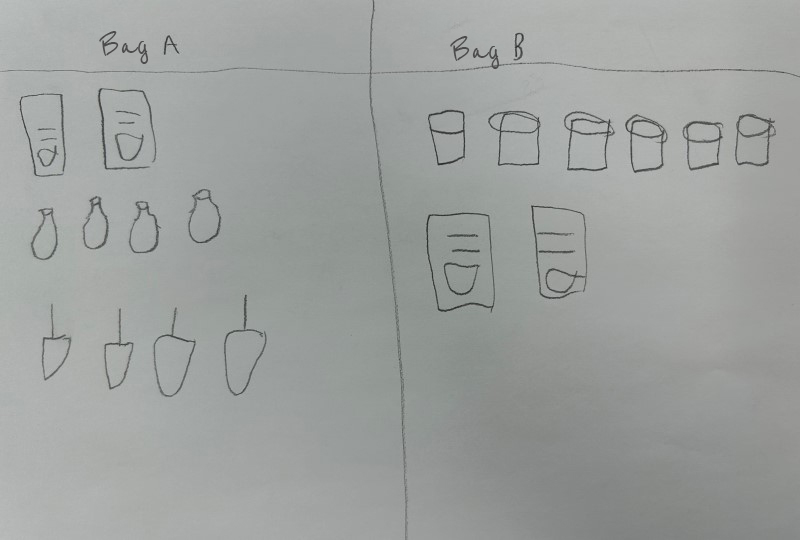
Goody Bag A:

4 spinning tops, 4 balloons and 2 decks of cards
Goody Bag B:

6 kaleidoscopes and 4 decks of cards
- How many of each kind of element are in the goody bags?
Ask students to suggest a way to represent the contents of the goody bags without using the objects themselves and without using numbers. Most students will suggest drawing the objects. Continue the discussion to find other possible representations.
Give each student a large sheet of paper. Have them draw a line down the center of the paper to divide it in half, then write "Goody Bag A" and "Goody Bag B" at the top of each section.
Ask students to represent the contents of each goody bag in different ways. If they choose to draw the objects to represent them, emphasize that it is not necessary to focus on the exact representation of objects.
Circulate and Ask Questions
Circulate among the students and provide support as necessary, by asking questions such as:
- You have represented the objects with drawings. Could you now represent them differently?
Sample representations include:
|
Representation Modes |
Drawings |
|
Drawings |
 |
|
Letters |
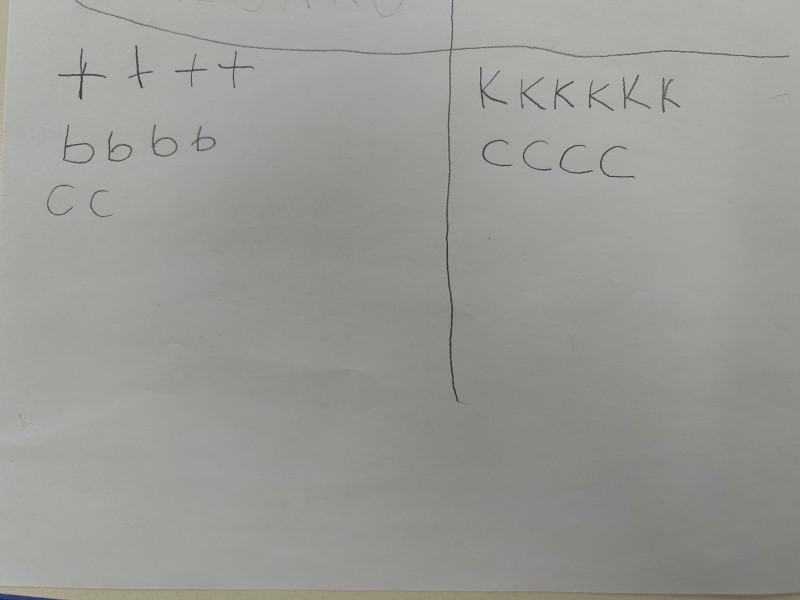 |
|
Words and drawings |
 |
Invite students to present and explain their representations, whether they are conventional or not; for example, one student indicates that they have chosen to represent the four spinning tops with the letter “D”, since it is the fourth letter of the alphabet. Support this student to understand the ineffectiveness of the representation by asking them to explain how one could symbolize the four balloons.
Once students have completed the various representations, ask for volunteers to present them to others. Ask them questions to compare and relate the various representations, such as:
- What is similar between the drawing and letter representations? Between the letter and word representations? (They represent the same quantities of objects.)
- What is different between the representations? (The mode of representation differs, either drawings, letters or words)
Active Learning (Exploration)
Duration: approximately 45 minutes
Review with students the contents of each goody bag and the representations made (drawings, words, letters) during the warm-up. If the ten frame was not used to represent the quantities of objects in the goody bags, suggest that students use it to represent the quantities of objects in Goody bag A.
Model the following example: I represent the four spinning tops in goody bag A by drawing a dot in four of the boxes in the ten frame.

By using the ten frame, students are introduced to a more symbolic representation of a number of objects, which calls on their capacity for abstraction.
Give each student two ten frames and ask them to represent the contents of one of the goody bags on one frame and the other bag on the second frame.


|
Possible Observations |
Possible Interventions |
|
To represent the objects, students draw them or write words or letters in each box of the frame. 
|
Point out to students that they have already represented objects in this way on their large paper. Invite students to come up with a more effective way to represent the objects in their ten frame. If necessary, remind students that quantities can be represented in a ten frame using dots. |
|
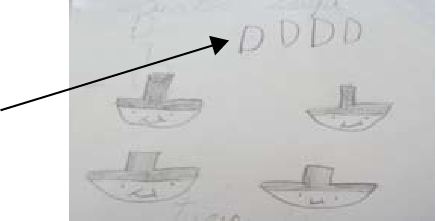
Some students use a single colour to represent the different objects in the ten frame. Others add the first letter of the object's name next to each dot. 
|
Encourage students to use a different colour for each kind of object, pointing out that it is difficult to distinguish between kinds of objects if they are all represented by the same colour. Point out that the coloured dots make it easier to see the quantity of each object. 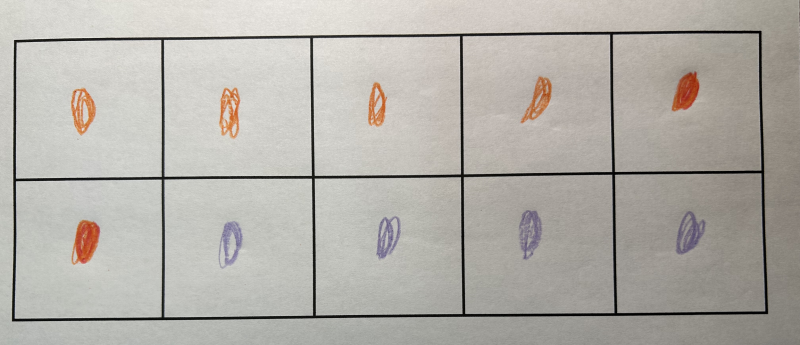
|
Present one of the ten frames with dots that correctly represent the contents of Goody Bag A. Encourage students to relate the number of dots in the frame to the amount of elements in Goody Bag A by asking questions such as:
- How many green dots are there in the ten frame?
- Which objects in the bag are represented by the green dots?
- Are there the same amount of dots as balloons?
- Can you recognize them in the ten frame?
- How many dots are there in the ten frame?
- How many elements are in the Goody Bag A?
Point out to students that the number of dots in the ten frame is equal to the number of objects in the Goody Bag A.
Next, present a ten frame with dots that correctly represent the contents of Goody Bag B and ask the same questions to relate the number of dots in the frame to the number of elements in the bag.
Then ask students to represent the amount of objects in each goody bag using two different number sentences. A number sentence is a symbolic expression that represents a relationship.
Some possible number sentences for each goody bag include:
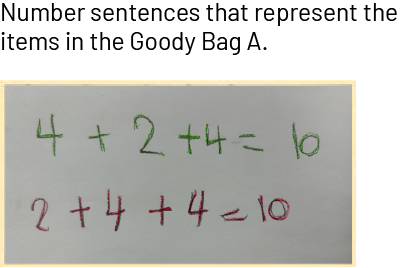
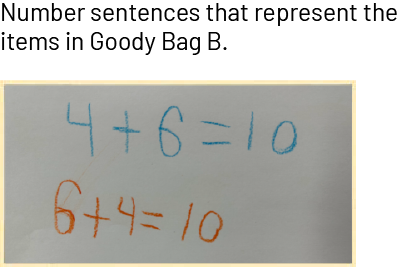
It is important to represent the same equality situation with different number sentences. In this way, students will understand that the = sign is not only used to introduce an answer to an operation; it also expresses the relationship that exists between the numbers or expressions on either side of it.
|
Possible Observations |
Possible Interventions |
|
The student writes number sentences that do not represent the quantities of objects in the goody bags. |
Ask the student what the numbers represent in their number sentences. Ask the student to count the spinning tops in the Goody Bag A and write the number corresponding to that quantity. Continue this questioning for the balloons and the deck of cards. Ask the student to name the sign they should write to indicate that these quantities are collected in the same goody bag (the + sign) and the sign they should write to indicate that the expression is the sum of all the objects collected (the = sign). |
|
Some students fail to write the + or = signs. |
Ask students to read their number sentences aloud. Point out that they have said plus and equals, but that the corresponding symbols do not appear in their number sentences. Ask them to add them in the appropriate places. |
|
Students write only one number sentence. |
Suggest that students change the order in which the objects were counted and write a new number sentence. |
Consolidation of Learning
Duration: approximately 30 minutes

Ask a student to present one of their number sentences corresponding to the contents of the Goody Bag A and to explain the meaning of the symbols; for example, in the number sentence 4 + 4 + 2 = 10:
- The first 4 represents the number of balloons.
- The second 4 represents the number of spinning tops.
- The 2 represents the number of decks of cards.
- The + sign represents the collection of objects in the Goody Bag A.
- The sign = means that the quantities represented on either side of the sign are equal.
Ask another student to write and explain a different number sentence to represent the objects in the Goody Bag A. If no one has come up with a different sentence, move the decks of cards.
Then ask a student to come up and write a number sentence that represents this other situation, that is 2 + 4 + 4 = 10 or 10 = 2 + 4 + 4.
Encourage students to compare the sentences 4 + 4 + 2 = 10 and 2 + 4 + 4 = 10 by asking questions such as:
- Do the two number sentences represent the contents of the Goody Bag A?
- Are the two number sentences true? How do you know?
Note: This question prompts students to check whether the numerical expressions on either side of the equal sign represents the relationship it indicates. If so, the number sentence is said to be true.
If necessary, suggest that a student use one of the pictures or objects in the goody bag to demonstrate.
Introduce other number sentences or have a student change the order of the objects, write the corresponding number sentence, and show how it represents the objects in Goody Bag A.
Follow the same process to write the number sentences that represent the contents of Goody Bag B; for example, depending on which object is chosen first (the kaleidoscopes or the deck of cards), the number sentences might be:
6 + 4 = 10
4 + 6 = 10
If students explain that the objects are already together, they could also write the number sentences:
10 = 4 + 6
10 = 6 + 4
It is important to present the different number sentences that represent the same equality situation to help students understand that a relationship can be represented in different ways.
Then ask students questions related to concrete and symbolic representations of the contents of the two goody bags such as:
- Do the two goody bags contain equal amounts of elements? How do you know? (Yes, since each bag contains a total of 10 elements.)
For each of the goody bags, choose a number sentence that represents its contents and combine these two sentences to form a new one; for example, combine the sentences 2 + 4 + 4 = 10 and 6 + 4 = 10 to form the sentence 2 + 4 + 4 = 6 + 4.
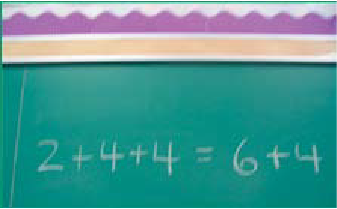
Write this sentence on the board and ask students questions such as:
- Are the numerical expressions 2 + 4 + 4 and 6 + 4 equal? How do you know? (Because each represents the contents of one of the goody bags and we know that each bag contains 10 elements)
When the quantities of the two goody bags are compared, the situation is one of equivalence.
To justify the equality, some students might point out the relationships between the numbers on either side of the = sign by saying, "There is a number 4 on each side of the = sign. The expression 2 + 4 that is on the left side is equal to the 6 that is on the right side."
Extension: New Surprises!
This activity helps students deepen their concept of equality by constructing various representations of a given equality situation. Repeating this type of activity throughout the year helps students see equality as a relationship between numerical expressions on either side of the = sign.
Put 10 small elements into resealable plastic bags in advance, making sure to include at least four different kinds of elements in each bag.
Form teams of two. Give each team one of the plastic bags containing 10 small objects, a paper plate, a large sheet of paper and a ten frame. Ask the teams to arrange the contents of their bag on the plate and represent the quantity of objects in different ways, as they did with the Goody Bags A and B in the learning situation.
Examples of possible representations include:

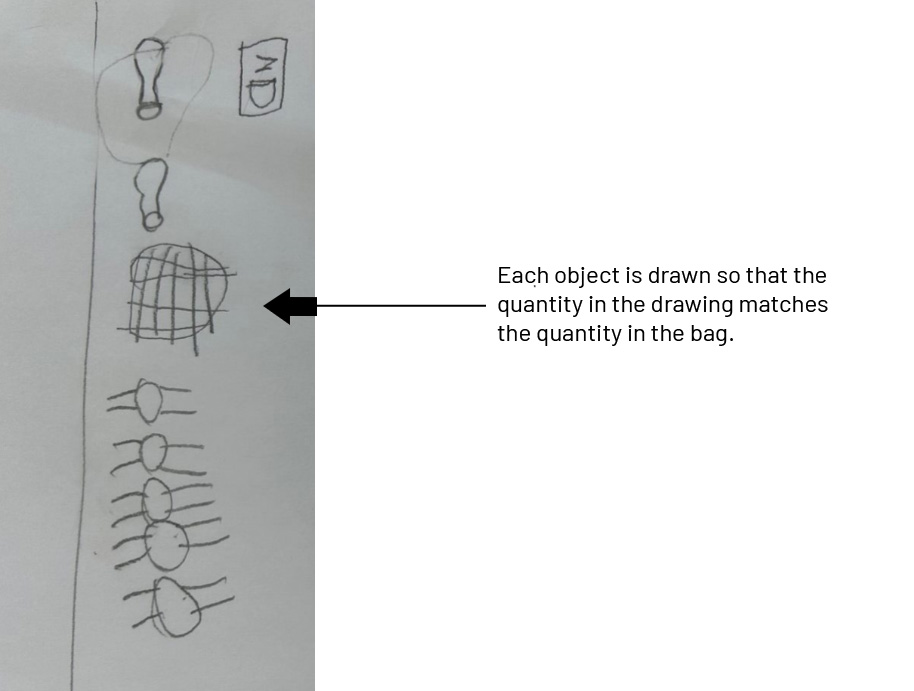


Circulate and Ask Questions
Invite students to share their reasoning by asking questions such as:
- Why did you group the same objects together? (To make the same kinds of objects easier to count)
- How do you represent the quantities of each kind of object?
- How are your representations similar? How are they different?
- What symbols could represent the quantities of objects?
- Is this number sentence true? How can you tell?
- Can you write another number sentence to represent the same objects? What is it?
As a class, review the various types of representations used by the students, following the same type of approach and questioning used during the learning situation. Ensure that they make the connection between the concrete representation and the number sentence. Target the modes of representation that the students did not use in order to explain them again.
Compare one team's number sentence, such as 2 + 2 + 1 + 5 = 10, with the number sentence that represented the objects in the Goody Bag B (4 + 6 = 10) and write them on the board side by side.
Ask questions such as:
- What is similar about the two number sentences? (Both represent a situation of equality involving 10 objects.)
- How do the two number sentences differ? (One of the sentences represents a situation of equality comprising four kinds of objects, while the other represents a situation of equality comprising two kinds of objects.)
- Is the sentence 2 + 2 + 1 + 5 = 4 + 6 true? (It is true because the numerical expressions on either side of the = sign are equal to 10.)
Differentiated Instruction
The learning task can be modified to meet the different needs of the students.
|
To Facilitate the Task |
To Enrich the Task |
|
Ask students to represent situations of equality through drawings. Ensure that they use the terms "is equal to" and "more" when explaining their representation. |
Have students create similar equality situations and present them to the class. Invite students to write number sentences for another student to illustrate using concrete materials. |
Follow-up at Home
A family member describes a possible situation of equivalence or equality using the vocabulary submitted by the teacher. The student must determine whether the statement is true or false and explain their answer. Two suggested statements are:
- The number of windows in the house is equal to the number of doors. (This is a possible situation of equivalence.)
- The total number of blue marbles and red marbles in your collection is 18. (This is a possible tie.)
Students can also play the game of representing number sentences written on cards with objects; for example, a parent presents a card with 5 + 3 = 8 on it and asks the child to represent the situation with round and square buttons or other objects (e.g., spoons and chopsticks) (this is an equality situation)
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Fascicule 2, Situations d'égalité, p. 129-142.
