C1.1 Identify and describe the regularities in a variety of patterns, including patterns found in real-life contexts.
Skill: Recognizing a Variety of Patterns
Non-Numeric Patterns
Repeating Patterns
The repeating pattern is created when the elements that make up the pattern core repeat in the same order. Students must learn to recognize the beginning and end of the pattern core; for example, in the photo below, the student who created this pattern shows, with a space between the pattern cores, that the orange bead indicates the beginning of the core and the red bead indicates the end.
In addition, it is important to have students "read" the pattern by naming and touching each consecutive element of the core so that they realize the repetition.
From kindergarten through the end of primary, the patterns that students learn to explore and create must be increasingly complex.
Here is a suggested approach to teaching repeating patterns:
- Observe a pattern with a single attribute and a two-element core.
First explore a pattern core that has only one attribute and whose core consists of only two elements. The attribute could be motion, position, sound, shape, or colour.
Example
In the pattern shown above, the attribute is position: one element on all fours and one element standing with arms outstretched constitute the pattern core.
Note: Colour change is easier to recognize and describe when a pattern is constructed with concrete materials, especially using objects that all have the same shape, such as beads on a necklace, algebra tiles, or interlocking cubes.
- Change the attribute.
Then explore patterns with another attribute such as shape or size, while still having two elements in the pattern.
Example 1
In the pattern shown above, the attribute is the shape. The two elements, the sailboat and the balloon, constitute the pattern core.
- Modify the structure of the pattern.
Explore more complex patterns by adding more elements to the pattern or more attributes. Students will then face a cognitive challenge that will lead to new learning.
Example 2
The following pattern has two attributes, shape and colour, and a three-element core, blue rectangle, blue rectangle, orange triangle. Its structure is AAB.
Continue by introducing a third shape or colour; for example, the following pattern also includes two attributes (shape and colour) and a three-element pattern (blue rectangle, red triangle, yellow oval). However, its structure is more complex, because there are three colours instead of two and three shapes instead of two. The pattern core is ABC.
Note: At the beginning of the math period, introduce patterns that have cores already explored so that students can locate them more easily and effectively.
- Change the mode of representation.
Present patterns that have the same structure but are constructed with different representations, and then test whether students recognize that they have the same structure. For example, present two patterns composed of different concrete materials, such as beads and interlocking cubes, or, as in the pictures below, two patterns, one of which is a concrete representation (a pattern of positions) and the other a semi-concrete representation (a pattern of drawn objects). When students can justify that the two patterns have the same structure, they are at a higher level of abstraction in their algebraic reasoning.
6 children make a sequence of repetitive motif with their body. They alternate between a standing and kneeling position on the floor, repeated 3 times. ball position. ‘’The legend illustrates ‘’ sequence with a position of ‘’A’’ ‘’B’’.A drawing of a series of objects, 2 crossed hockey sticks and a puck, repeated 3 times. The legend illustrates ‘’sequence of objects drawn with a structure ‘’A’’ ‘’B’’.
- Explore patterns with a missing element.
An interesting challenge to present to students is the identification of a missing element in a pattern.
Examining the pattern to determine what element is missing from the beginning, middle, or end of a pattern increases their understanding of relationships. Many such explorations help students understand the pattern as a whole that contains several pattern cores, rather than as a pattern of changing elements without any relationship.
Example 3
The missing bead is a red bead.
- Identify false leads.
Recognizing that an attribute can be a false lead in a pattern helps develop algebraic reasoning.
Example 4
Pattern A:
In this pattern, the colours used are not an attribute of the pattern. Therefore, students should ignore the colour attribute and stick to the shape attribute (triangle or circle).
Pattern B:
In this pattern, the different shapes and colours create false leads that must be eliminated in order to discover the attribute, that is the position of the base (shape placed on a flat side or on a vertex).
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 30-33.
Growing Patterns
The simplest growing patterns are those in which term 1 is composed of one element and each of the subsequent terms increases by only one element (example A). Patterns where term 1 is composed of more than one element and where the subsequent term increases by one element (example B) or by more than one element (example C) are more complex.
Examples
When students construct the shapes of a growing pattern in a rectangular arrangement, as in example C, they are simultaneously working on multiplication.
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 40-41.
Number Patterns
Very early on, students become aware of patterns in their environment, in nature, in the objects around them. This is why it is possible to introduce number patterns as early as Grade 1 . At the same time, students develop their sense of number, can count in intervals and backwards, and later acquire the concept of addition as a grouping of objects. All of these concepts have an important connection to learning number patterns.
"Because our number system is built on a system of patterns and predictability, students must be able not only to identify the patterns that they see but also to give reasons and evidence for why the patterns exist." (Economopoulos, 1998)
As students begin to explore the base-10 number system, which is in fact the decimal system, they discover that the digits 0-9 are repeated when they count beyond 9 (10, 11, 12, 13, 14, 15…). Seeing and justifying this pattern in the decimal system enhances understanding of number sense and groupings (units, tens, hundreds, etc.). For example, when skip counting by 2, starting at 16, students observe a predictable regularity in the numbers 16, 18, 20, 22, 24, 26, 28, 30, 32.…This is a first step toward exploring multiples of 2. This understanding also leads to an ability to skip count from any number. Similarly, when students count by 5s, they quickly recognize a pattern, that is, that the units digit alternates between the digit 0 and the digit 5 (5, 10, 15, 20…). They can generalize this discovery informally by saying that any number that is a multiple of 5 will end in 5 or 0.
As is the case when learning concepts related to non-numeric patterns, it is by developing the ability to recognize, among other things, number patterns in addition and subtraction that students in the primary grades build their algebraic thinking. The approaches described above for developing this skill also apply to numeric patterns.
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 49-51.
Skill: Describing the Pattern Rules in a Variety of Patterns
Non-Numeric Patterns
Repeating Patterns
During an activity, it is important for teachers to ask students relevant questions to get them to verbalize their observations, identify relationships, and explain how they identified the rule.
To help students establish an intuitive understanding of the structure of the pattern, teachers encourage them to verbalize the elements of the repeating pattern; for example, to describe the pattern of movements snap, snap, raise your arm in front of you… , teachers ask them to say out loud: "snap, snap, raise…"; to describe a pattern of beads forming a necklace, they are asked to touch the beads while naming them aloud: "blue bead, purple bead, red bead…" When students describe their pattern, it is important to explain the relationship between the patterns (the elements of the pattern are represented in the same order) and use appropriate math vocabulary.
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 37-38.
Sample Questions
- What are the attributes used to create the pattern?
- What are the elements of the pattern?
- Explain why this is a pattern.
As an example, they may describe the following pattern as follows: "The attributes are shape and position. The pattern has three elements: a triangle pointing up, followed by a triangle pointing down, followed by a sun. The three elements of the pattern always repeat in this order."
Students can also record their understanding. Examples of factors to record include:
A sequence of a repetitive motif of 3 elements. A sequence of a repetitive motif of 3 elements. The sequence has 9elements. The 9elements are numbered from one to nine, by the ranking. The elements are also represented by letters, ‘’A’’, ‘’B’’, ‘’C’’ the letters represent a structure of the sequence. A tracing waves line is placed under each motif. The regularity: A triangle pointing towards the top, triangle pointing towards the bottom, and a sun is represented always in the same order.
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 37.
Growing Patterns
Building on the change in shapes from one term to the next, students describe the pattern rule informally; for example, students might describe the rule in the patterns below as follows:
Pattern A:
"The pattern rule is that you always add a star to the shape in the previous term."
Pattern B:
"The pattern rule is that you always add a term of three squares below the squares in the previous term."
Note: The pattern is described according to the number of elements and not according to the attributes which do not influence the growth of the pattern.
To describe the pattern specifically and see the relationships between each term, students must also be able to justify the arrangement of the elements that make up each shape. Questioning helps students develop their ability to reason and recognize relationships. To help them, ask questions such as:
- Can you explain how the shape in term 3 of Pattern A was constructed? of Pattern B?
- How will the shape in term 4 of Pattern B be constructed? What must be done to obtain the shape at the 5th position of Pattern A? of Pattern B?
- Where did you discover a pattern rule in Pattern A? in Pattern B?
Students should explore growing patterns using concrete materials. Then, students discuss ways to create them as well as the relationships they see. Students also explain their understanding of the pattern rule: "Each tree is built by adding a rectangle to the trunk of the previous tree."
To describe what happens next, students can also make notes on their work, as in the following example.
The age of the tree and the number of shapes to represent each year.
In growing patterns, there is also a relationship between the term of each shape and the number of elements in each. This relationship is a very important mathematical concept, demonstrated with a table of values and leading to a more formal generalization in Grade 3, the formulation of the functional relationship.
Although in Grade 1 students are not required to define functional relationship, informal discussions dealing with the relationships between shapes and the number of elements that make them up can take place in determining the pattern rule and extending the pattern.
The study of patterns, whether they are non-numeric or number patterns, is the cornerstone of understanding regularities. Exploring patterns is a task that requires manipulation, interventions, and discussions that will help each student take a first step into the world of algebra.
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 44-46.
Vocabulary Related to Non-numeric Patterns
Here are some explanatory notes on the mathematical vocabulary related to non-numeric patterns.
Non-numeric pattern: set of shapes or objects arranged according to a pattern rule
|
Repeating Pattern |
Growing Patterns |
 |
|
|
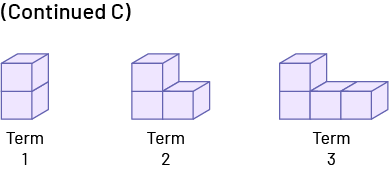
Attribute: a characteristic that describes an object that we observe or manipulate. In pattern A, the attributes that describe the pattern are shape and colour. |
In a growing pattern, attribute analysis is no longer important, since the focus is on pattern growth. |
|
Term: each shape, object, or motion that makes up a non-numeric pattern. In Pattern A, each of the plane shapes is a term. |
In patterns B and C, each of the shapes is a term. |
|
Pattern core: the smallest part of a pattern from which the pattern rule is created. Pattern core in Pattern A: a blue rectangle followed by a green trapezoid and then an orange triangle. Each object that makes up the pattern is called a pattern element. |
Element in Pattern B: a square (shape in term 1). Element in Pattern C: two superimposed cubes (shape in term 1). |
|
Pattern rule: uniform criterion that defines a pattern and helps to determine each of its terms. Pattern rule in Pattern A: repeat the blue rectangle, green trapezoid, orange triangle pattern, always in the same order. |
Pattern rule in Pattern B: a square is added to the previous shape. Pattern rule in Pattern C: a cube is always added to the bottom term of the shape in the previous term. |
|
Structure: letters representing the pattern rule of a repeating pattern. In Pattern A, each element of the pattern can be identified by a letter: blue rectangle (A), green trapezoid (B), orange triangle (C). The structure of Pattern A is therefore ABC. |
|
|
Position: Where each term is located in a pattern, indicated by a number. It is used to help describe the functional relationships in a pattern and to predict the next terms in the pattern without having to extend it. In Pattern A, there is a blue rectangle in the 1st, 4th and 7th terms, a green trapezoid in the 2nd, 5th and 8th terms, etc. |
In patterns B and C, each shape has its position: the first shape is in the 1st position, the second shape is in the 2nd position, etc. |
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 29.
Number Patterns
The terminology described above for describing non-numeric patterns also apply to number patterns.
Example
Pattern C:
2, 4, 6, 8, 10
"The pattern rule is that you always add 2 to the previous term."
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 50.
Vocabulary Related to Number Patterns
Here are some explanatory notes on the mathematical vocabulary related to number patterns.
|
Number pattern: Set of numbers arranged in an order and pattern |
|
|
Rule: a uniform phenomenon that defines a patterns and helps determine each of its terms. In the primary cycle, the pattern rule is studied as it applies to addition and subtraction (as of Grade 1 ) or multiplication and division (as of Grade 3 ). |
|
|
Pattern rule in Pattern A: each term is always 5 more than the previous term. |
Pattern rule in Pattern B: each term is always 5 less than the pervious term. Pattern with a subtraction pattern rule |
|
Pattern with an addition pattern rule Pattern A: 5, 10, 15, 20, 25, 30… Term: each number that makes up a number pattern. |
Pattern B: 30, 25, 20, 15, 10, 5, 0 |
|
Position: Where each term is located in a pattern, indicated by a number. It is used to help describe the functional relationships in a pattern and to predict the next terms in the pattern without having to extend it. |
|
|
In Pattern A, the number 5 is in the 1st position, the number 10 is in the 2nd position, etc. |
In Pattern B, the number 30 is in the 1st position, the number 25 the 2nd position, etc. |
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 50.
Skill: Recognizing and Describing Patterns Found in Everyday Life
Young children have a natural curiosity and interest in the patterns around them. Patterns can be literary, artistic, musical, scientific or numeric. Patterns are found in many events, such as the succession of seasons and days of the week, the growth of living things, and daily activities; in rhymes and songs, such as rhythm, rhymes, and number of syllables; in stories with repeated structures, such as Goldilocks and the Three Bears; in music, such as the different sounds of instruments; in gestures, such as standing, crouching, or sitting; and in the world we have built, such as traffic lights, odd and even house numbers. Repeating patterns decorating objects, such as vases, clothing, and jewelry, from various cultures are also good examples of patterns.
Source: Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 26.