At a Glance...

C2.2 Determine whether given pairs of addition and subtraction expressions are equivalent or not equivalent.

Skill: Determining Whether Given Pairs of Addition and Subtraction Expressions are Equivalent or Not Equivalent

---

Two addition and subtraction expressions are equivalent when they represent the same quantity. 

Two addition and subtraction expressions are not equivalent when they represent different quantities. In a number sentence, the equality sign with a slash through it (≠ ) is a symbol that represents this non-equivalence or two different quantities.

Note: The equal sign should not be interpreted as the "answer", but rather, that both parts on either side of the equal sign are equal, therefore creating balance. 

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

When students reason algebraically, they analyze numbers, symbols, quantities, and operations, and then generalize.

A significant mathematical step in the development of algebraic thinking is to understand that a situation of equality can be represented using different models.

Students may use a variety of modes of representation. Mathematical relationships can be represented using concrete or visual (semi-concrete) materials, symbols, or oral descriptions. When students represent an algebraic situation using one or more modes of representation, they use a variety of models such as tables, number grids, or number lines. These models help them organize, record, and communicate their thinking as they explore situations of equality. Representing numerical expressions using concrete, visual (semi-concrete), or symbolic models, along with oral description, facilitates observation of relationships and contributes to the development of algebraic thinking. The different representations help students to internalize algebraic concepts.

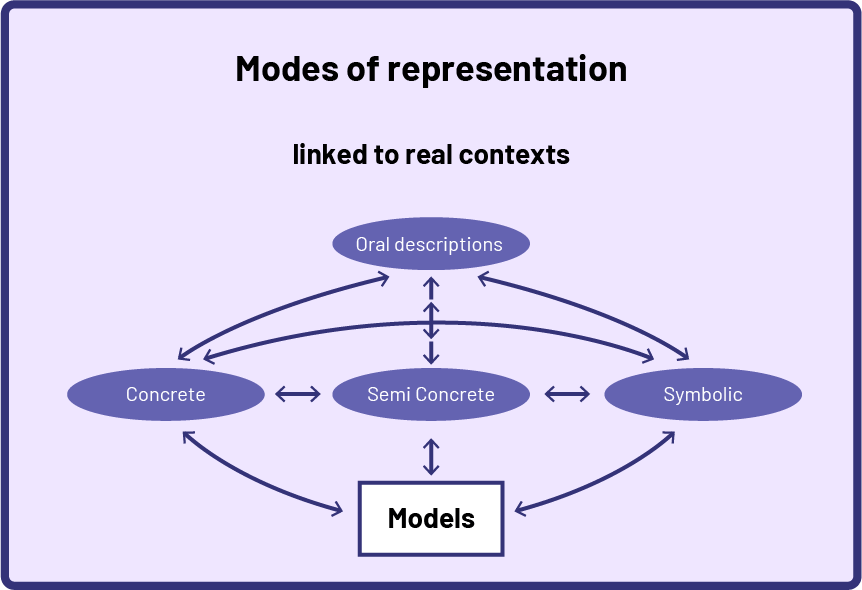
Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 14-15.

Prior to coming to school, young children have used expressions of equality in their play and daily lives, such as "My friend has more or less or the same number of toys as me". At school, they are learning about numbers and associating quantities with them. It is important for students to explore and represent equality relationships in a variety of ways before expressing them symbolically in a number sentence. A sentence such as 3 + 4 = 7 becomes meaningless when the focus is first on the symbols used. Before performing calculations, students need to explore numbers using models to support and develop their reasoning skills. Symbol meaning is developed by using various representations of equality and inequality relationships. Teacher questioning, combined with manipulation of symbols and numbers in a variety of strategies, will help students make conjectures and subsequently generalize.

In algebra, students need to grasp the concepts of equality and inequality in order to understand equivalence as a relationship between two quantities. They must first explore these concepts using concrete materials.

From the time they enter school, most students can already compare quantities and recognize situations of equivalence; for example, more than, less than, as much as, is equal to, is not equal to.

When faced with a situation of equality represented by symbols, teachers should have students recognize the relationship between the two numerical expressions on either side of the = sign; for example, in the number sentence 18 = 10 + 8, 18 and 10 + 8 are two representations of the number 18, and the = sign is the symbol that shows the equality relationship between these representations. Understanding this relationship will help students later manipulate the numbers, the unknown, or the variables in an equation more effectively.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 28-30.

Meaning of the Equal Sign

The symbol for equality is a universally known sign, but often misinterpreted by many students who perceive the = sign as the symbol that always precedes, in number sentences, the answer to a calculation from left to right.

When students later explore the symbolic representation of an equality or equivalence situation, such as the equation 4 + 3 = ◯ + 2, they believe that the number 7 should be inserted into the unknown box, since it represents the answer to the operation 4 + 3, appearing to the left of the = sign. When asked to process the number 2, they add it to 7, as if the number sentence simply continued from left to right: 4 + 3 = 7 + 2. They do not perceive the = sign as a symbol of the equality or equivalence relationship between the expressions on either side of it.

This misconception stems, in part, from the fact that students are essentially exposed to equality situations presented through simple number sentences such as 4 + 1 = 5. To address this misconception, teachers can:

• ask students, Is 4 + 1 the same as 1 + 4?

Note: This type of questioning promotes a better understanding of the concepts of relationship and equality.

• present different types of number sentences to help students explore the concept of the = sign as a relationship.

It is important to encourage students to be explicit about their own understanding of the = sign These exchanges will ensure that teachers can check this understanding and that students can use mathematical arguments, one of the foundations of algebraic thinking.

In a problem-solving approach, the use of concrete and visual (semi-concrete) materials, as well as models, helps students recognize and represent situations of equality, equivalence, and inequality.

Moreover, it is only after having manipulated various models several times with the goal of recognizing situations of equality or inequality, that students will be able to approach the purely symbolic representation (number sentence) of the situation.

In addition, to determine the nature of the relationship between the quantities, they must understand that the expressions on either side of the = sign are data to be analyzed, not just calculated.

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3^e année, Fascicule 2, Situations d'égalité, p. 36-40.

Example

Determine if these pairs of numerical expressions are equivalent.

6 + 2

4 + 4

Pan Balance

Source: translated from En avant, les maths!, 1^re, CM, Algèbre, p. 3.

Double Number Line

Knowledge: Numerical Expression

---

A numeric or algebraic representation of a quantity. An expression may include numbers, variables, and operations.

Examples:

3 + 9

5 – 4

10

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3^e année, Fascicule 2, Situations d'égalité, p. 32.

Knowledge: Pairs of Equivalent Numerical Expressions

---

Two addition and subtraction expressions are equivalent when they represent the same quantity.

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

For example, looking at a ten frame filled with 7 blue and 3 red counters and another filled with 8 blue and 2 red counters, the student sees that the expression 7 + 3 is equivalent to 8 + 2, since both frames represent a quantity of 10.