C2.1 Identify when symbols are being used as variables, and describe how they are being used.
Skill: Describing Ways and Situations where Symbols are Used as Variables
Symbols in Everyday Life
At a very young age, students live in a world where ubiquitous signs communicate, by their nature, a clear message or define a precise function; for example :
- traffic lights dictate behaviour (red means stop or no go; green means go);
- the characters on the doors of the washrooms give information as to the purpose of the room;
- in the daycare centre, several symbols indicate where to store toys, clothes, etc;
- a song or rhyme announces a specific activity (ror example, snack time, rest time, tidying up);
- WHMIS safety signs make children aware of the toxicity of cleaning products;
- road signs, logos, and commercial signs quickly become meaningful to children.
The acquisition of these symbols is experiential, without the symbols being systematically taught, memorized, or recited. Despite their arbitrary nature, the symbols quickly become familiar to children. Thus, each symbol used in a given context is associated with a specific meaning. However, they may be subject to other interpretations if used in new contexts.
Symbols in Mathematics
Mathematical symbols represent fundamental concepts that underlie the learning of mathematics and algebra. Many of these concepts, which have become familiar to adults, are often introduced to students prematurely in out-of-context situations or without prior explanation. In order to explain them clearly and accurately, it is therefore essential to create situations in which students have time to become familiar with the symbols and to appropriate their meaning.
| Symbols in Mathematics | Examples |
|---|---|
| Symbols Designating Quantities - Numbers (Indo-Arabic Numerical or Graphic Symbols) |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Symbols Representing Fundamental Operations - Signs that designate the four operations in numeration |
– + × ÷ |
| Symbols that Establish Relationships The sign that indicates equality Signs that indicate inequality |
= ≠ > < |
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 52.
Meaning of Symbol in Algebra
As students have varied and meaningful experiences, they develop symbol sense. Symbol sense is a level of mathematical understanding that encompasses number sense.
(H. Picciotto and A. Wah, "A New Algebra: Tools, Themes, Concepts," Journal of Mathematical Behaviour, vol. (H. Picciotto and A. Wah, "A New Algebra: Tools, Themes, Concepts", Journal of Mathematical Behaviour, Vol. 12, No. 1, 1993, p. 42, as cited in Ontario Ministry of Education, Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année – Modélisation et algèbre, fascicule 2, 2008, p. 65).
Luis Radford (2001) sees learning algebra as the appropriation of a new mathematical way of thinking and acting that involves the production and use of symbols. These symbols carry meaning for students as they are explored in contextualized mathematical activities.
A key component of algebraic reasoning is the ability to recognize and explore relationships that link various quantities. These relationships are represented by various symbols that students must learn to use appropriately.
In the primary grades, a dash, geometric shape, or other symbol in an equation represents, to students, an unknown quantity (for example, in the equation 3 + Δ = 5, the triangle is a symbol that represents the quantity 2). Proper use of a box or dash is a first step toward the more formal symbolism of algebra.
Students with a fair understanding of this will be able to more effectively interpret or manipulate the literal symbols commonly used in algebra to represent the unknown or variable in the junior grades. Symbol meaning plays an important role in the development of algebraic thinking. Understanding of symbols is a function of students' maturity and diversity of experience.
Here are some points to consider to help students develop a sense of the symbol:
- Introduce students to symbols in challenging and realistic contexts to enable them to grasp their meaning and, ultimately, to understand the concepts behind them.
- Encourage students to identify the elements to be represented in a problem situation, to choose an appropriate mode of representation, and to use personal symbols.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 53.
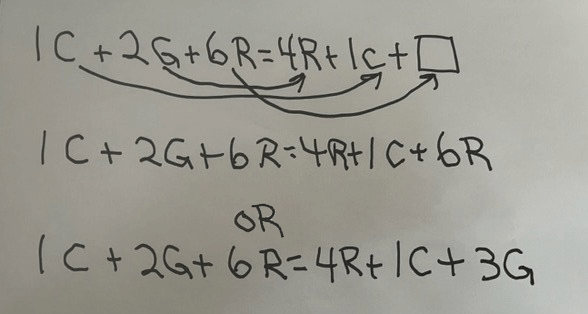
Above, students use the first letter of each animal's name to formulate the number sentence; for example, T represents the toad, F represents the frog, and T represents the tree frog.
Encourage students to determine when and how to use symbols (for example, represent a missing quantity, in an equation, with a square).
Provide activities that require students to make connections between various modes of representation, discuss these connections, and justify them using mathematical arguments.
To understand the meaning of the symbol, students should:
- describe relationships using various modes of representation before exploring them symbolically;
- make connections between representations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 51-54.
It is also important to have students observe that there are quantities that do not change in their daily lives. This awareness will help them better grasp the concept of constant later in their learning. Finding quantities in their everyday lives that stay the same and quantities that can change will help students understand the concept of variable.
Source : The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
The efficient use of different modes of representation is part of a progressive pathway integrated into the Numbers strand. Its purpose goes far beyond the simple mechanical use of symbols and memorization "tricks" in algebra. Rather, it is about developing the ability to perceive patterns, generalize relationships, and solve problems.
Here is an example of an authentic problem situation illustrating a progressive path towards developing an understanding of the meaning of the symbol.
| Pathway to Develop an Undestanding of the Meaning of the Symbol | Examples |
|---|---|
| Present the situation and the data. | A student could state the following: "There are 10 people on the bus after the first stop and 15 people after the second stop. How many people got on the bus at the 2nd stop? got off?" |
| Propose a conjecture. | I believe that the number of people getting off the bus is always smaller than the number of people getting on the bus. |
| Represent the problem situation using concrete materials or drawings. | Students use cubes to represent people.
Students represent the people with drawings. 
|
| Gradually move away from semi-concrete representations and use personal symbols to communicate understanding of the situation. | In the picture below, the student has chosen the following symbols as labels:
p for people; d for people getting off the bus; m for people boarding the bus. 
|
To develop a sense of the unknown, students need to explore a variety of authentic situations that engage meaningful data and promote the transition from the concrete to the abstract.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 54-55.
Symbols can be used to represent and describe, in an abstract way, the pattern created in a concrete or semi-concrete representation.
For example, students use a semi-concrete representation to illustrate a pattern of bricks placed vertically and horizontally.
Example 1
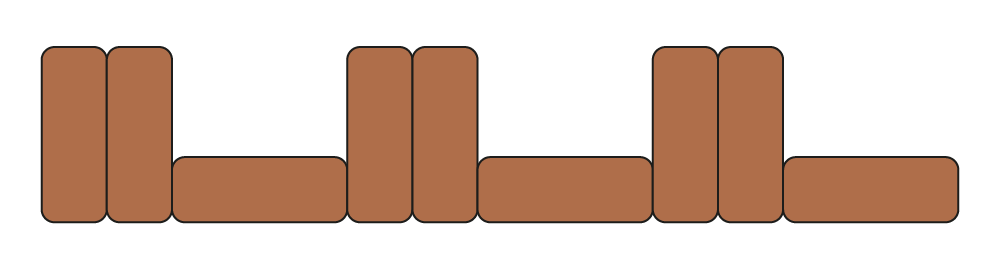
Students quickly realize that it takes a long time to draw the bricks and then decide, as a result of this realization, to use symbols such as D (standing) and C (lying) to represent the standing brick and lying brick elements in the suite and describe its structure.
By using symbols that are meaningful to them, students deepen their understanding of a symbolic representation. The symbols then become an efficient way to represent the situation and the observed pattern.
Example 2
A model using blocks. The pattern is composed of two blocks in a vertical position and one block in a horizontal position, repeated 3 times. Each vertical block is labelled D and horizontal block is labelled C. The motif is ‘D’’,’’D’’,’’C’’, repeated 3 times.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 17.
Knowledge: Symbol
Graphic sign that represents a number, an operation, a relationship.
Note: In an equation, if the same symbol appears more than once, its value is the same, For example,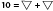 
. Two different symbols in
an equation can have varying values. For example, 
, the two symbols can have values of 10 and 10, 19 and 1, etc.
Knowledge: Variable
A term (symbol or letter), in an equation, that can be replaced by one or more values.
In the equation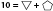 
Or 10 = x
+ y, the shapes or letters are variables, because the quantities are unknown.
Source : En avant, les maths!, 2e année, CM, Algèbre, p. 2.
Knowledge: Constant
The quantities that remain the same are called constants.
Example
Looking at the pattern below, we notice that in each term/shape, what stays the same, the constant, is the group of 8 purple squares. What changes are the groups of blue squares.
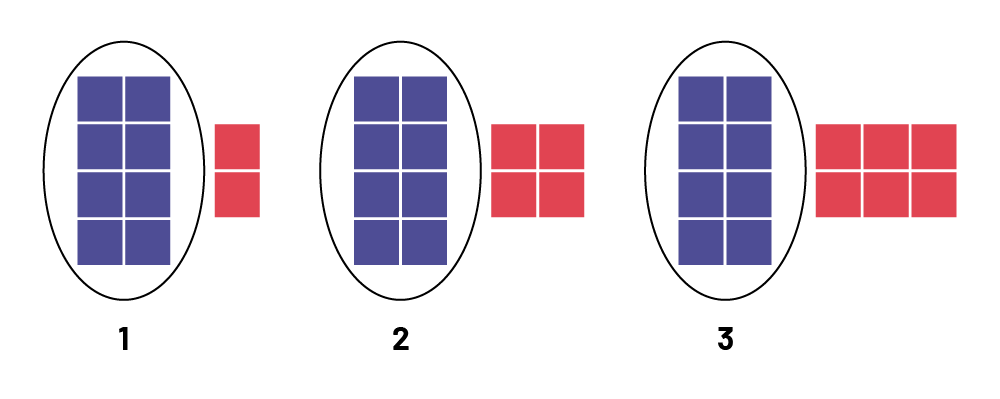
Source : En avant, les maths!, 2e année, CM, Algèbre, p. 2.