C2.2 Determine what needs to be added to or subtracted from addition and subtraction expressions to make them equivalent.
Skill: Determining What Needs to be Added or Subtracted to Make Expressions Equivalent
Two sets of numerical expressions are equivalent when they represent the same quantity.
Two numeric expressions are not equivalent when they represent different quantities. In a number sentence, the equal sign with a slash through it (≠) is a symbol that represents this non-equivalence of two different quantities.
Note
The equal sign should not be considered a symbol that announces the answer to an equation, but as a symbol that shows equality between two quantities.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Through algebraic reasoning, students analyze numbers, symbols, quantities, and operations, then generalize them.
A significant mathematical step for students in developing their algebraic thinking is to understand that an equality situation can be represented using different models.
Students can use different modes of representation. Mathematical relationships can be represented using concrete or visual (semi-concrete) materials, symbols, or oral descriptions. Students who represent an algebraic situation using one or two modes of representation use a variety of models such as tables, number grids, or number lines. These models help them organize, record, and communicate their thinking as they explore situations of equality. The representation of numeric expressions, using concrete, visual (semi-concrete) or symbolic models, along with oral description, facilitates the observation of relationships and contributes to the development of algebraic thinking. The different representations allow students to internalize algebraic concepts.
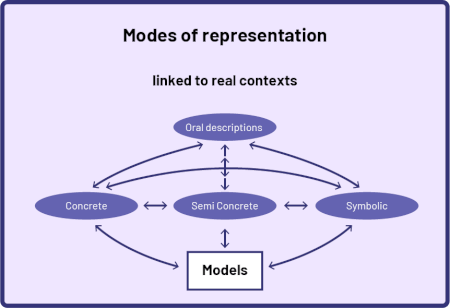
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 15.
It is essential that students explore and represent equalities in a variety of ways before expressing them symbolically in a number sentence. A sentence such as 20 + 15 = 35 becomes meaningless when the focus is first on the symbols used. Before performing calculations, students need to explore numbers using models to support their reasoning. Symbol meaning is developed through the use of various representations of equal and unequal relationships. Teacher questioning, combined with manipulation of symbols and numbers using different strategies, will allow students to propose conjectures and subsequently generalize.
In algebra, students need to grasp the concept of equality and inequality in order to fully understand equivalence as a relationship between two quantities. They must first explore these concepts using concrete materials.
When faced with a situation of equality represented using symbols, it is important to get students to recognize the relationship between the two numerical expressions on either side of the equal sign. In the number sentence, for example, 18 = 6 × 3, the 18 and the 6 × 3 are two representations of the number 18, and the = sign is the symbol that demonstrates the equality relationship between these representations. Understanding this relationship will enable students to manipulate the numbers, the unknown or the variables in an equation more effectively.
Meaning of the Equal Sign
The equal sign is universally recognized. However, students often misinterpret the equal sign, perceiving it as a signal to perform an operation from left to right.
When students later explore the symbolic representation of a situation of equality or equivalence, such as the equation 4 + 3 = ◯ + 2, they believe that the number 7 should be inserted into the unknown box, since it represents the answer to the operation 4 + 3, appearing to the left of the = sign. When asked to process the number 2, they add it to 7, as if the number sentence simply continued from left to right: 4 + 3 = 7 + 2. They do not perceive the = sign as a symbol of the equality or equivalence relationship between the expressions on either side of it.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 36.
This misconception stems, in part, from the fact that students often see equality situations presented using simple number sentences such as 4 + 1 = 5. To address this misconception, it is possible to:
- ask students, "Is 14 + 6 the same as 6 + 14?
Note: This type of questioning promotes a better understanding of the concepts of relationship and equality. - introduce students to different types of number sentences to explore the concept of the equal sign as a relationship. Here are some of them:
| Types of Number Sentences | Examples |
|---|---|
| Sentences with only one number on either side of the = sign. | 5 = 5 60 = 60 |
| Phrases that encourage the use of a strategy, such as compare terms. | 8 - 7 = 9 - 8 |
| Sentences that use a property, for example the commutative property. | 5 + 10 = 10 + 5 |
| Sentences where one of the numerical expressions has more than two terms. | 5 = 2 + 2 + 1 55 = 25 + 25 + 5 |
| Sentences with different operations on each side of the = sign. | 29 + 2 = 33 - 2 |
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 37.
The equal sign represents the relationship between the expressions and not the symbol that systematically precedes the answer to an operation.
It is important to encourage students to express, explicitly, their own understanding of the equal sign. These exchanges allow students to check their understanding and to use mathematical arguments, one of the foundations of algebraic thinking.
Skill: Creating a Situation of Equality
To develop algebraic reasoning, it is also important for students to explore situations of inequality. These situations require the use of strategies to establish equality (make it true) and require a higher level of thinking (analysis). Restoring the equality of a situation is done first with concrete materials and then with symbols.
Important! Students should use concrete materials to re-establish an equality, compare quantities, explore equivalent relationships, then re-establish equality between quantities.
Creating Situations of Equality with the Help of Concrete Materials
The examples below show the use of various types of concrete materials to establish equality. It is important to always present situations to students in a meaningful context.
Example 1
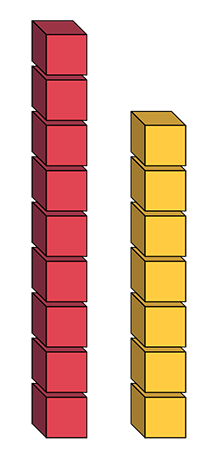
Ask students to build two towers of different colours and heights using interlocking cubes. Then ask them to describe the inequality; for example:
- The towers are not equal because the red tower is taller than the yellow tower. It has two more cubes than the yellow tower. The quantity 9 cubes is larger than the quantity 7 cubes (9 > 7), so there is inequality (9 ≠ 7).
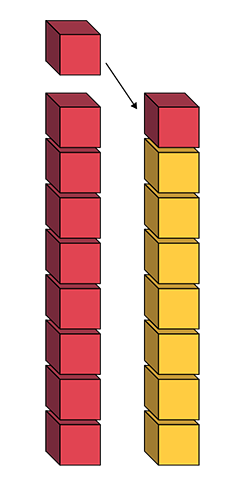
Then ask students to describe what they can do to establish equality; for example:
To establish equality, I can transfer a cube from the red tower to the yellow tower so that both towers have the same height.
Later, students can more easily represent this situation (re-establish equality) symbolically: 9 - 1 = 7 + 1.
To establish equality, I can also remove two cubes from the red tower so that it is equal to the yellow tower.
Students can also represent this situation symbolically: 9 - 2 = 7.
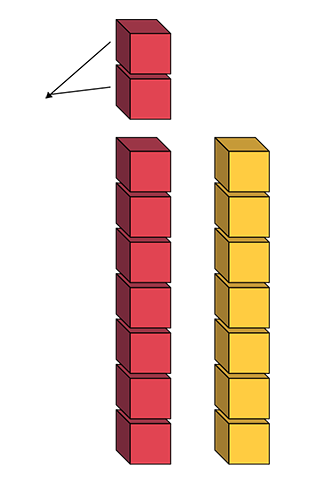
Example 2
Present students with two towers like those shown below and ask them to explain the inequality represented that 3 + 6 ≠ 7; for example:
- The red and blue tower has two more cubes than the yellow tower. Since the quantity 3 + 6 cubes is greater than the quantity 7 cubes (3 + 6 > 7), there is inequality.
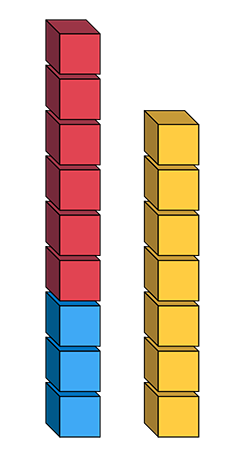
Invite students to re-establish equality using the same strategies as in the previous example, and then represent it symbolically with number sentences; for example:
- I remove a red cube from the first tower and place it on the second tower (6 - 1 + 3 = 7 + 1).
- I remove a blue cube from the first tower and place it on the second tower (6 + 3 - 1 = 7 + 1).
- I remove two red cubes from the first tower (6 - 2 + 3 = 7).
- I remove two blue cubes from the first tower (6 + 3 - 2 = 7).
- I remove one blue and one red cube from the first tower (6 - 1 + 3 - 1 = 7).
Example 3
Using a ten frame, students must recognize and explain the inequality before seeking to establish equality.
Present students with the following problem:
A gardener plants tulip bulbs in two beds. 5 red tulip bulbs and 5 yellow tulip bulbs are planted in one bed. 3 orange tulip bulbs and 6 blue tulip bulbs are planted in the other bed.
Ask students to first represent 5 + 5 in a ten frame, then 3 + 6 in another ten frame. Draw students' attention to the inequality (5 + 5 ≠ 3 + 6), then to the nature of the inequality relationship between the two frames (5 + 5 > 3 + 6).
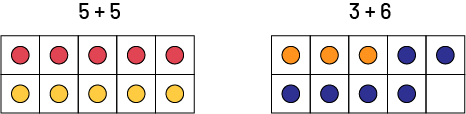
Ask students to demonstrate what the gardener could do if they wanted to have an equal amount of tulips in each bed.
Strategy 1: Students establish equality by removing a token from the frame that has the most tokens; for example:
The gardener could remove 1 red tulip bulb from the bed containing 10 tulip bulbs.

Strategy 2: Students establish equality by adding a token to the frame that has the fewest; for example:
The gardener could add 1 blue tulip bulb to the bed containing 9 tulip bulbs.
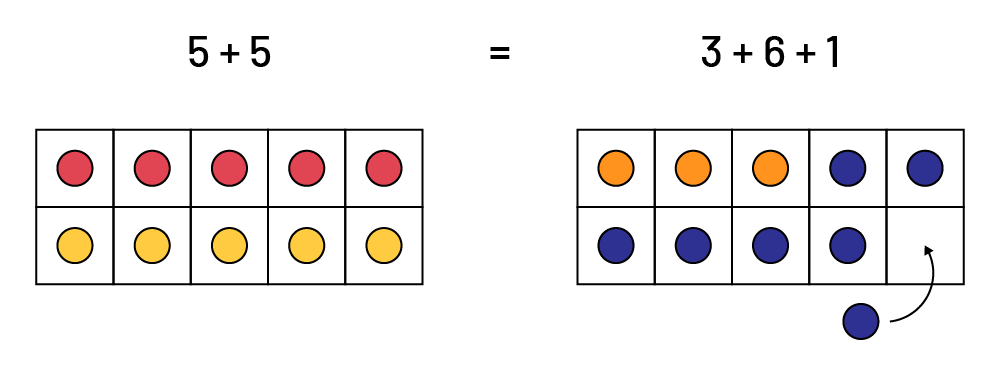
Once balance is achieved, students will see that although there are not the same amount of each colour of tokens, the two ten frames ultimately contain the same amount of tokens, hence equality. In addition, the number sentence will allow them to confirm the equality of the two numeric expressions.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 44-46.
Students can also use hops on a number line to show what needs to be added so that the two expressions are equivalent.
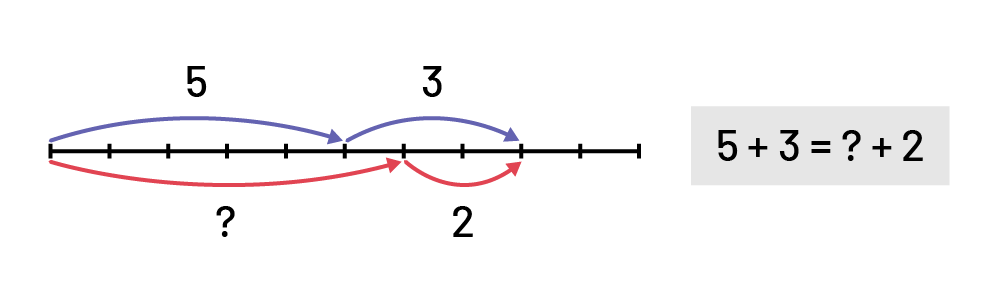
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
When using a balance model, the representations of the addition or subtraction expressions are manipulated until there is an identical representation on both sides of the balance.
When using a balance scale, the objects on the scale are manipulated until the scale is level.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Knowledge: Numeric Expression
An expression that contains only numbers linked together by operations. All numbers are, by definition, numeric expressions.
Examples
3 + 9 – 2
5 × 4
10
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 32.
Knowledge: Pairs of Equivalent Numeric Expressions
Numerical expressions are equivalent when they produce the same result, and an equal sign is a symbol denoting that the two expressions are equivalent.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
For example, by observing two leaps of 5 and 20 on one number line and two leaps of 20 and 5 on another number line, the student sees that the expression 5 + 20 is equivalent to the expression 20 + 5, since the sum of the two expressions represents a quantity of 25.
