C2.3 Identify and use equivalent relationships for whole numbers up to 100, in various contexts.
Activity 1: Property Exploration
Explore the Commutative Property
Example 1
Ask students to make a necklace by stringing 5 red beads and 2 blue beads, then suggest they write the corresponding number sentence.
(5 + 2 = 7)

Have students turn the necklace and write the corresponding number sentence.
(2 + 5 = 7)

Then suggest that students compare the two number sentences and answer the following questions:
- What do you notice about the order of the beads?
- What do you notice about the amount of beads?
- Why is the quantity the same in both cases?
- Change the amount of beads on the necklace and write two number sentences. Compare the sentences. What do you notice?
- If you do the same process using a large amount of beads on the necklace such as 100, 300, or 500, what can you say about the equality situations you observe?
Note: Repeat the activity, asking students to move to look at the necklace in the other direction instead of turning it.
Example 2
Ask students to determine if the number sentences below are true or false without performing any calculations.
6 + 3 = 3 + 6
45 + 34 = 34 + 46
67 + 89 = 89 + 67
3 × 8 = 8 × 2
After introducing them to each number sentence, ask students the following questions:
- How can you tell if this sentence is true or false?
- What do you notice about the terms in this equality?
Explore the Role of the Number 0 in Addition
Present students with six toys and ask them to count them. Cover the toys with a cloth and tell them that you will add a mystery number of toys.

Pretend to add toys, but do not add anything. Remove the cloth and ask students the following questions:
- How many toys are there now?
- How many toys did I add?
Ask students to write a number sentence to represent the situation. (6 + 0 = 6)
Repeat the activity adding 6 toys to 0 toys to represent 0 + 6 = 6.
Point out to students that since 6 + 0 = 6 and 0 + 6 = 6, we can conclude that 6 + 0 = 0 + 6 and make the connection with the commutative property of addition.
Encourage students to propose a conjecture about the role of the number 0 in addition, and then ask them questions such as:
- Could you apply your conjecture to other numbers? Give it a try.
- Could you apply your conjecture to all numbers? Why?
Explore the Role of the Number 0 in Subtraction
Ask students to write a number sentence to represent the situation. (8 - 0 = 8)
Encourage students to propose a conjecture about the role of the number 0 in a subtraction, and then ask them questions such as:
- Could you apply your conjecture to other numbers? Give it a try.
- Could you apply your conjecture to all numbers? Why?
Explore the Role of the Number 1 in Multiplication
Present students with a plate containing eight marbles (or other objects, such as chips, buttons, cubes) and ask them to count them.

Point out that this is a group of eight marbles and write the corresponding number sentence:
1 × 8 = 8
Repeat the activity using sets with eight different items (for example, one group of eight students, one group of eight pencils).
Point out that 1 × 8 is always equal to 8.
Repeat the same activity using other numbers.
Then present students with an activity that has eight groups of one element (for example, eight students each have a bicycle) to represent 8 × 1 = 8.
Point out that since 1 × 8 = 8 and 8 × 1 = 8, we can conclude that 1 × 8 = 8 × 1 by linking to the commutativity property of multiplication.
Encourage students to propose a conjecture about the role of the number 1 in a multiplication, and then ask them questions such as:
- Could you apply your conjecture to other numbers? Give it a try.
- Could you apply your conjecture to all numbers? Why or why not?
Explore the Associative Property
Example 1

Introduce students to three train cars constructed with interlocking cubes of different colours.

Ask the students to help Mr. Bontrain, the conductor, who wants to combine two cars without changing their order.
Represent each possible situation with the cubes and write the corresponding number sentence. To avoid using parentheses, use boxes to illustrate the cars.
Note: Cars can be grouped in two ways:

Ask students the following questions:
- Are there other possible car groupings? How do you know?
- What is the sum of the cubes that form the train in each case?
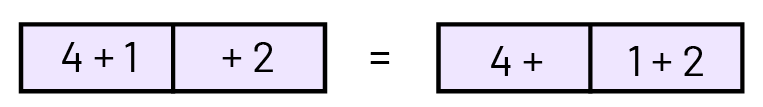
- How is it possible that the sum remains the same even if we have different car groupings?
- Would this work using three other numbers? Demonstrate this using a double open number line and a number sentence.
Ask students to explain their observation to someone.
Afterwards, ask students the following question:
- What could you write in your collective math journal about what you discovered today?
Repeat the activity using a larger number of cars.
Note: Students who are familiar with the commutative property, might change the order of the terms to be added (for example, 4 + 2 + 1). If so, ask them to justify why the order can be changed. Otherwise, simply mention that the order of the cars cannot be changed, since they are attached to the track in this way.
Example 2
Ask students to check the equality of the number sentences below without performing any calculations.
(7 + 4) + 6 = 7 + (4 + 6)
46 + (34 + 67) = 46 + (34 + 46)
67 + (89 + 103) = (67 + 89) + 105
For each sentence, ask students questions such as:
- How can you tell if this sentence is true (or false)?
- What must be done to make this sentence true?
Source: tranlsated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 86-100.
Activity 2: Using Strategies to Develop Algebraic Thinking
Add a Mystery Number
Group students into teams of two. Have them build two towers, each with six interlocking cubes.
Ask students the following question:
- What do you notice when you look at the two towers?
Ask them to add any number of cubes to the towers, while making sure to keep the game tied.
Ask each team to explain how they maintained the tie. Then write the answers on a chart.
Example
| Group | Height of the Towers at the Beginning | Added by Student A | Added by student B |
|---|---|---|---|
| 1 | 6 | 3 | 3 |
| 2 | 6 | 4 | 4 |
| 3 | 6 | 1 | 1 |
| 4 | 6 | 5 | 5 |
| 5 | 6 | 2 | 2 |
Ask students to analyze the data. Draw their attention to the fact that the same amount must be added to each of the towers in order to maintain equality. Point out that this is true for all the quantities added.
Ask students to check if it is possible to add a quantity to a single tower and still maintain equality. Point out that the equality holds only if nothing is added (0 cubes).
Have one member of each team add a cube to their tower, then ask students the following questions:
- What do you notice now as you look at the two towers?
- What do you need to do to restore equality?
Note: Students should be able to see and explain the inequality before seeking to restore equality.
Have one member of each team add 2-5 cubes to their tower, as desired.
Invite the other member to re-establish the tie between the two rounds.
Ask each team to explain how they made the towers equal. Point out to students that each team had to add the same amount of cubes to the second tower as they added to the first tower to make them equal. Draw their attention to the fact that this applies to all the quantities added.
Decompose Numbers According to Positional Values
Introduce students to the number sentences below and ask them if they are true or false:
47 = 40 + 7
35 + 12 = 35 + 10 + 2
47 + 21 = 40 + 20 + 7 + 1
700 + 90 + 5 + 8 = 795 + 8
To encourage students to justify their answers, ask them the following questions:
- How can you tell if this sentence is true (or false)?
- Is it possible to check for equality using concrete materials (for example, ten frames, base ten materials, interlocking cubes)?
- How does this material help determine if the sentence is true (or false)?
- Is it possible to verify the equality without any concrete material and without doing any calculation? How can we do it?
Cancel Equal Terms or Expressions
Example 1
Write the following number sentence: 6 + 24 + 32 = 32 + 24 + 6
Ask students the following questions:
- Is this number sentence true or false? How do you know? (Some students will use the commutative property.)
- If I remove the numbers 32 on each side of the equal sign, does the equality remain true?
- If I remove the numbers 24 on each side of the equal sign, does the equality remain true?
Write the following number sentence: 6 + 24 + 32 = 32 + 20 + 4 + 7
Ask students the following questions:
- Is this number sentence true or false?
- How do you know that?
Example 2
Present students with the number sentences below and ask them to check whether they are true or false:
3 + 4 + 2 = 3 + 3 + 2
5 + 6 + 8 = 6 + 5 + 8
11 + 7 + 4 = 5 + 6 + 7 + 4
54 + 67 + 75 = 54 + 67 + 75
12 + 78 + 20 + 3 = 78 + 23 + 14
For each sentence, ask students the following questions:
- Is this sentence true or false?
- If you cancel terms that are the same on either side of the equal sign, is the equality still true? How do you know?
Compare Terms
Introduce students to the following number sentences:
9 + 8 = 10 + 7
34 + 67 = 35 + 66
23 + 48 = 26 + 45
Ask students to check, using a double open number line, if these sentences are true.
For each sentence, ask students the following questions:
- How can you say that this sentence is true?
- What terms did you compare?
- What do you notice about these terms?
- Can you compare the terms in another way?
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 101-108.
Activity 3: Representing Quantities to Understand Equivalence Relations
When numbers are decomposed, the parts are equivalent to their whole.
The various activities below help students understand that even though the quantity is broken down in different ways, it remains the same (for example, 50 = 25 + 25; 49 + 1 = 1 + 49; 20 + 20 = 10 + 10 + 10 + 10). The concrete and visual (semi-concrete) representations can later be combined with a symbolic representation.
Represent 90 cents or 90 dollars in various ways using different coins or play bills. If you do not have enough materials for all students, use the Ontario Mathies website.
Represent 75 using different leaps on a number line or a bead string or Rekenrek.
Mystery Number: Group students into pairs. Ask them to represent a number in different ways (concrete material, visual or semi-concrete, symbolic). Have students circulate around the classroom to see how other teams have represented their mystery number.
Activity 4: A Story of Adding, Joining and Comparing!
Summary
In this activity, students create and represent three different situations that correspond to the same given number sentence. These are an addition situation, a joining situation and a comparison situation.
Directions
Present students with a number sentence involving addition (for example, 7 + 2 = 9).
Create and represent, using manipulatives, three situations that correspond to the number sentence: an addition situation, a joining situation and a comparison situation.
Describe each situation in words.
Example
Addition Situation
In my bag, I have 7 field hockey cards. I add 2 more cards to my bag. I now have a total of 9 cards in my bag.
Joining Situation
For a class presentation, I bring 7 cards of field hockey players and my friend brings 2 cards. We group our cards together so that we have 9 to present.
Comparison Situation
On my desk are my 7 field hockey cards and my friend's 2 cards. Another friend has 9 baseball cards on his desk. We see that we have the same number of cards.
Note: The addition situation and the joining situation are examples of equality situations, while the comparison situation is an example of a situation of equivalence.
Provide students with manipulatives. Group students into teams of two. Give each team a card with a number sentence involving addition written on it.
Ask each team to create and represent, using manipulatives, three situations that correspond to this sentence (an addition situation, a joining situation, and a comparison situation) and to describe each one using words.
Invite a few teams to present their three situations and ask the other students to identify the addition situation, the joining situation, and the comparison situation.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 165-166.
