C1. Patterns and Relationships
Identify, describe, extend, create, and make predictions about a variety of patterns, including those found in real-life contexts.
Learning Situation: I'm Growing Up!
Duration: 90 minutes
Summary
In this learning situation, students will create and explore a pattern that has a repeating operation of addition. The students will analyze the pattern that the tree grows by each year over five years and represent its growth using a table of values. Students will use the pattern rule to extend and make predictions.
| Overall Expectations | Specific Expectations |
|---|---|
|
C1. Patterns and Relationships |
C1.1 Identify and describe repeating elements and operations in a variety of patterns, including patterns found in real-life contexts. C1.2 Create and translate patterns that have repeating elements, movements, or operations using various representations, including shapes, numbers, and tables of values. C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in patterns that have repeating elements, movements, or operations. |
Objective
The purpose of this learning situation is to have students:
- construct a table of values to build an understanding of the numbers in the table;
- describe the pattern rule by identifying the repeating operation occurring within the pattern;
- develop, and apply problem-solving strategies.
| Learning Situation | Prerequisites |
|---|---|
| In the primary grades, students explore various patterns and describe their regularity (repeating elements
or repeating operations) using words and symbols. Students use their pattern rule to extend patterns. In Grade
3, students also learn to represent a pattern using a table of values which can also help students with
noticing a repeating operation that exists between the numbers in the table.
In this learning situation, students will create, represent and analyze a pattern with a repeating operation. The ability to use various representations of a relationship is an essential component of algebraic thinking. |
To be able to complete this learning situation, students need to:
|
Materials
- sufficient quantity of pattern blocks for the whole class
- large sheets of paper (one or two per pair)
- felt-tip pens
- book The Two Trees
Mathematical Vocabulary
pattern, repeating pattern, repeating operation, repeating elements, pattern rule, attribute, similar, different, table of values, row, column, name of pattern blocks (e.g. trapezoid, rhombus)
Before Learning (Warm-Up)
Duration: approximately 30 minutes
Read the tale The Two Trees by Elisabeth Brami. It tells the story of two trees that, separated by the construction of a wall, will not be able to meet again until a few years later, when the small tree has grown. Discuss the story of the growing tree and the growth of trees in general.
Form teams of two. Provide them with pattern blocks and ask them to create a tree using two to five pattern blocks.
Circulate and observe. Once the trees have been built, tell the students to circulate from one team to another to observe the diversity of the representations (e.g., quantity, shape, arrangement of the pattern blocks chosen).
Examples
 |
 |
 |
 |
Ask students the following questions:
- How does a tree grow in nature? (Emphasize the development of the different parts of the tree)
- What makes it possible to see that a tree is growing?
- How can we show that our tree is growing?
Active Learning (Exploration)
Duration: approximately 30 minutes
Form teams of two and present the problem situation below as well as the criteria. Provide them with a sufficient quantity of pattern blocks.
Problem Situation
Show the growth of a tree for each year from one year to six years.
Criteria
- The tree is to be built with pattern blocks.
- Pattern should have a repeating operation (e.g., increase of pattern blocks from one year to the next).
- Ask students to solve the problem.
Examples
Simple pattern: the repeating operation is represented by the addition of a rectangle to the length of the tree trunk each year

More complex pattern: the repeating operation is represented by adding two triangles to the foliage each year and adding one rectangle to the tree trunk each year

Ask students the following questions:
- What pattern blocks did you use to create your one year old tree?
- What pattern blocks do you add each year to show its growth?
- How many pattern blocks of each shape (if any) do you add each year?
- How many pattern blocks in total do you add each year?
Ensure that each student can relate the age of the tree to the addition of pattern blocks and explain its growth.
Ask students to circulate around the classroom and observe the different representations of a tree's growth from one year to six years. Also have them identify the pattern blocks that have been added to represent its growth from year to year.
Select patterns for discussion during the consolidation. Select increasingly complex patterns to help students understand the pattern rule (i.e., how many pattern blocks are added from one year to the next). Be sure to choose some patterns that have the information needed to construct a table of values.
| Possible Observations | Possible Interventions |
|---|---|
| Even after questioning, some teams were unable to represent the tree's growth for six years. | Tell them to continue after the discussion or to proceed to the next step without completing the concrete
representation. Note: During the discussion, these students will have the opportunity to discuss and observe the different pattern rules and continue to build their representations. |
| Some teams create a pattern rule that is too complex to represent the tree from year to year. | Ask them to explain their pattern rule. If they can't, tell them to simplify it. |
| Some teams did not meet the criteria for steady growth. | Count with them the number of pattern block pieces for the one-year-old tree as well as for the two-year-old
tree. Ask them to say how many pieces were added to the two-year-old tree. Explain that this same amount must be added to the tree from year to year in order to meet the criteria for steady growth. |
|
Some teams represent the additions on the same tree rather than building it every year. 
|
Ask them how they will see the additions that have taken place each year. Say, "Where is the one-year-old,
two-year-old, three-year-old, etc. tree?" Also ask them to look at the growth of another team's trees and show that, in this way, the additions are easier to determine. |
|
Students grow the trees from right to left. 
|
Explain to students that a sentence is read from left to right. This way, everyone understands the same
thing. To read a pattern, do the same as in reading.
Ask students to represent their pattern on a piece of paper for discussion during the math exchange and to indicate with numbers how their tree grows. Several representations are possible. Some students will trace the shapes, others will draw them; the important thing is to respect the pattern. |
Examples
To show how the tree grows, some students only show the age of the tree.
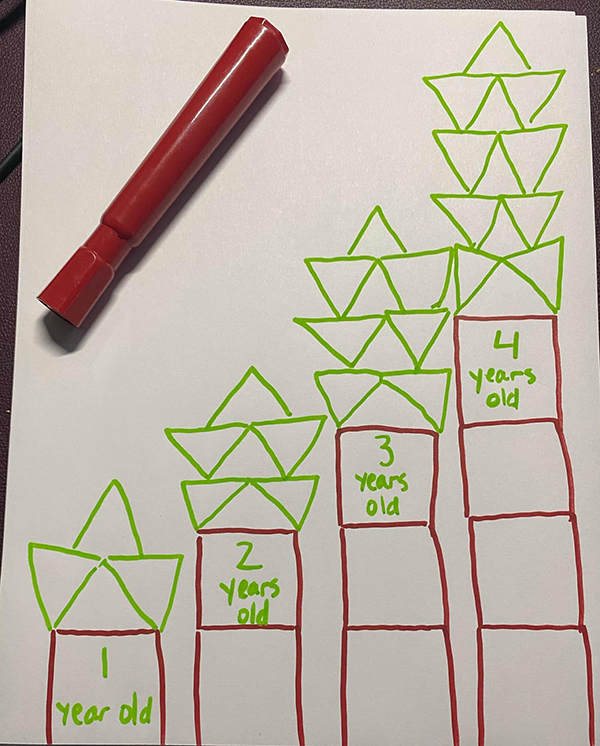
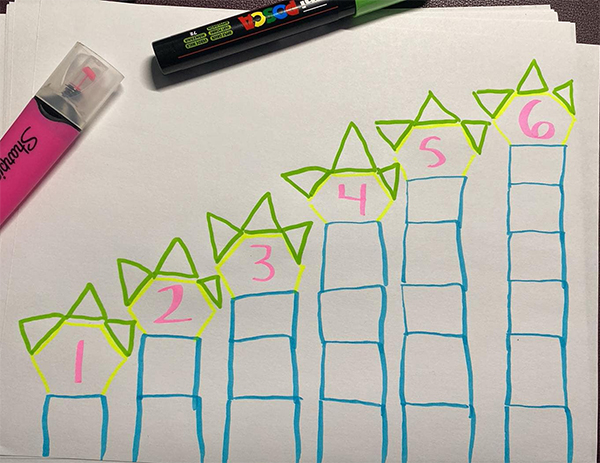
Other students indicate the age of the tree and the number of pattern blocks used each year.
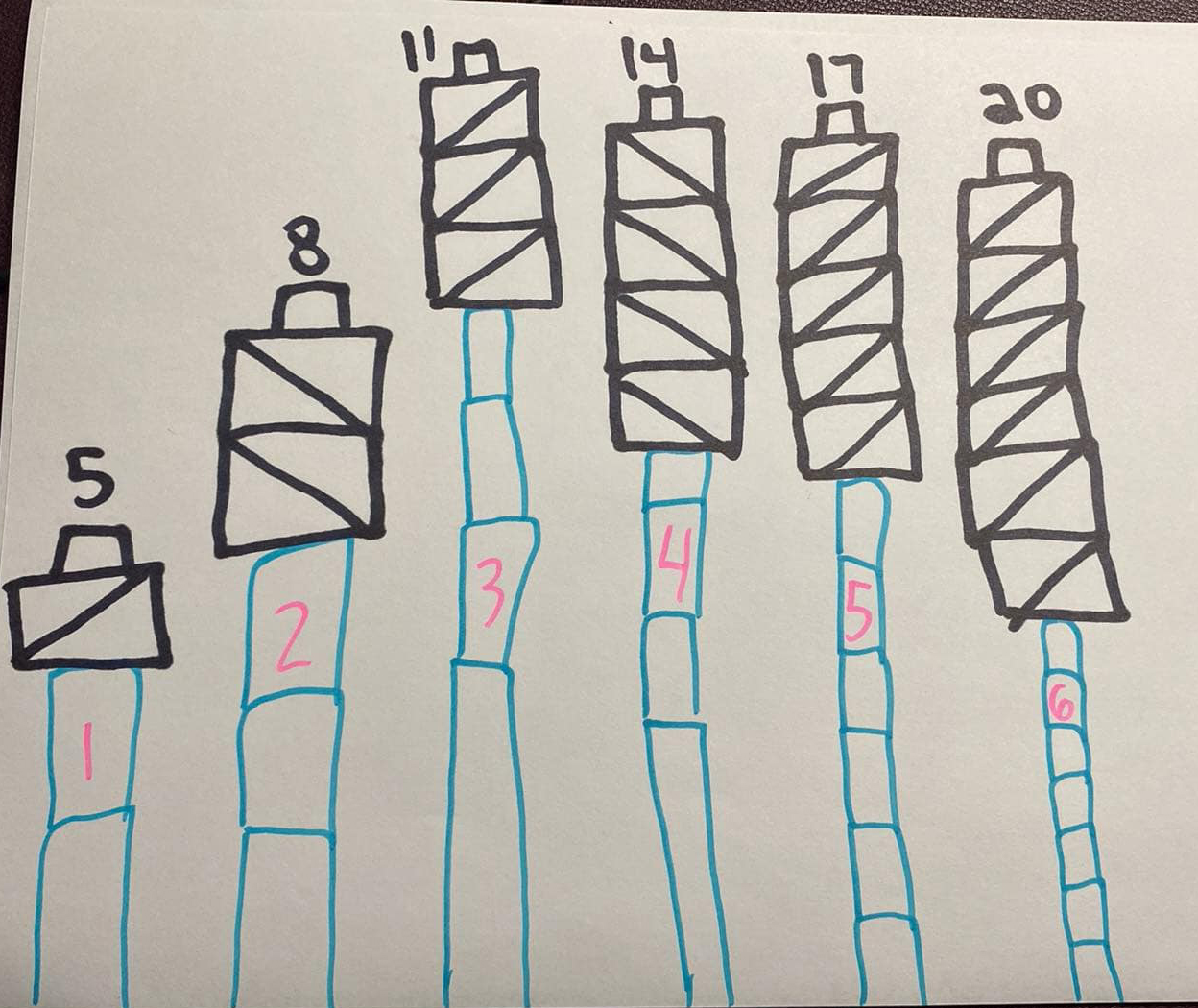
Other students report the number of each pattern block for each tree, the total number of blocks per year, and the age of each tree.
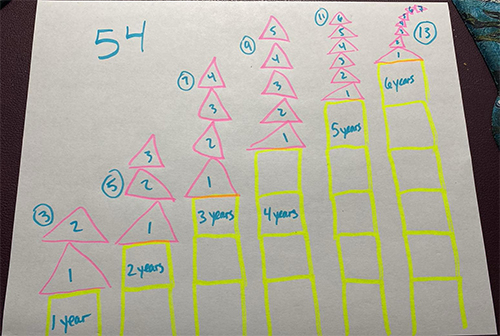
If no student states the total number of pattern blocks needed to show the growth of the tree each year, wait until the consolidation to ask them questions and have them write it down.
Consolidation
Duration: approximately 30 minutes
Mathematical Conversation 1
Display the selected pattern representations. Have students realize that the tree grows steadily from year to year, and that this growth is represented by the addition of the same number of pattern blocks being added on.
Ask questions such as:
- How many different pattern blocks is the one year old tree made of?
- What pattern blocks are added to the tree each year?
- How many pattern blocks of each shape are added to the tree from year to year?
- How many pattern blocks in total are added each year?
- What number pattern is created by adding pattern blocks each year?
- What is the rule for this pattern?
- What is the repeating operation in this a pattern?
- Can you predict the number of pattern blocks needed to build the tree at age 8? at age 10? How do you know?
Mathematical Conversation 2
Point out that the position number and the number of elements in each position are the values that go into the construction of a table of values. In this case, the position number is the year and the number of elements is the number of pattern blocks. For example, at one year old, the tree is built with four pattern blocks; at two years old, with six pattern blocks; etc. Support students in seeing the connection between the table of values and the pattern rule (for example, + 2, i.e. the addition of two pattern blocks each year).
Ask questions of students who have clearly indicated what the numbers represent on their drawings (the number of pattern blocks or the age of the tree). For example:
- How can the number of years passed be shown?
- How can you determine the total number of pattern blocks used each year?
- If you didn't have the drawings, how could you indicate what the numbers represent?
Draw a table of values on the board. Label the columns or rows (depending on the layout of the table of values). Connect the picture of each of the trees with the numbers that correspond with it in the table of values.
Invite students to come and fill in the table of values.
Have students extend the table of values to show the growth of the tree to eight years.
Extension 1: Let's Compare our Work!
This activity allows students to compare tables of values and consolidate their understanding of this representation.
Have each team display their work. Ask students to observe the different number patterns corresponding to the number of pattern blocks used each year.
Ask questions such as:
- Do any of the suites look the same?
- What is the same? What is different?
- Why do some patterns have different designs, but tables of values that are the same?
It is important for students to compare tables of values and the rules that emerge from them. Identifying and comparing rules from different patterns allows students to generalize. Even if the numbers in some patterns are different, it is possible that the patterns have the same rule.
In the pictures below, each pattern has a +1 pattern rule.

Extension 2: Association Activity
In this activity students compare different patterns and explore their similarities and differences.
Form teams of two. Ask them to illustrate an increasing number pattern of their choice on a strip of paper. Then give them a second strip of paper and ask them to construct the table of values that represents the pattern. Collect all the strips of paper.
Group three teams together. Give each group three strips of paper illustrating non-numeric patterns (patterns illustrated by other teams) and the corresponding tables of values. Ask them to match the table of values to the corresponding pattern and to justify their answers.
Differentiated Instruction
The learning situation can be modified to meet the different needs of the students.
| To Simplify the Task | To Enrich the Task |
|---|---|
|
Ask students to:
|
Ask students to:
|
Follow-Up at Home
Students can take their work (drawing of the six trees and table of values) home and continue the investigation of tree growth.
Suggested approach:
- choose a piece of furniture (table, chair, etc.) to represent the wall that separates the two trees in The Two Trees;
- place the six-year-old tree on one side of the "wall";
- determine the number of years of growth required for the tree to grow beyond the "wall";
- extend the table of values to the specified number of years;
- Back in class, students present and explain their extended table of values using appropriate vocabulary.
