C3. Coding
Solve problems and create computational representations of mathematical situations using coding concepts and skills.
Learning Situation: Endless Cookies
Duration: 140 to 150 minutes
Summary
Students will be able to practice multiplication facts as well as the array by creating a code for the baker's machine.
| Overall Expectation | Specific Expectations |
|---|---|
| B2. Operations Use knowledge of numbers and operations to solve mathematical problems encountered in everyday life. |
B2.4 Demonstrate an understanding of algorithms for adding and subtracting whole numbers by making connections to and describing the way other tools and strategies are used to add and subtract.
B2.6 Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays. |
| C3. Coding Solve problems and create computational representations of mathematical situations using coding concepts and skills. |
C3.1 Solve problems and create computational representations of mathematical situations by writing and executing code, including code that involves sequential, concurrent, and repeating events.
C3.2 Read and alter existing code, including code that involves sequential, concurrent, and repeating events, and describe how changes to the code affect the outcomes. |
| High-Impact Instructional Practices | Description |
|---|---|
| Learning Goals, Success Criteria and Descriptive Feedback | Post the success criteria in the classroom for students to refer to as they work. Throughout the activity, take time to circulate around the classroom and observe what students are doing. Question students about their work and provide descriptive feedback related to the posted success criteria. |
| Math Conversations | In the scenario, students will have the opportunity to discuss possible solutions to the code. In this discussion, they will be able to listen to the opinions of other students, explain their reasoning and add to the ideas of others. |
| Tools and Representations | Students will practice their knowledge of multiplication and solidify their learning by representing it using arrays. They will be able to model various situations visually and compare them with other representations. Effective use of tools and representations means that different representations are valued and connections are made between them. |
| Prerequisite Knowledge and Skills |
|---|
|
Learning Goals
At the end of this learning situation, the student will be able to:
- write and execute the code for an array;
- add one or more loops in its code to make it more efficient;
- use numerical multiplication facts to help arrange pastries efficiently on a baking sheet.
| Skills | Criteria |
|---|---|
| Knowledge and Understanding |
|
| Thinking |
|
| Communication |
|
| Application |
|
Materials
computer and application or coding software of your choice
Note: The examples in this learning situation were created using Scratch.
Mathematical Vocabulary
array, code, sequential events, simultaneous or concurrent events, repeating events, loop, variable
Before Learning (Warm Up)
Duration: approximately 30 minutes
Assessment can be carried out through…
Introduce students to the photo below. Ask them what questions they might have about the photo or what observations they might make about the photo (I notice, I wonder).
Sample questions:
- How many cookies are there in total?
- How can you determine the number of cookies without counting them one by one?
- I see a baking sheet with 4 rows of 5 cookies and a baking sheet with 2 rows of 3 cookies.
- I think there are 20 cookies on the bottom baking sheet, even though I can't see the top row, because 4 × 5 = 20.
| Possible Observations | Possible Interventions |
|---|---|
| The student does not know where to start. | What do you have to do now? What do you see? |
| The student is unable to make connections to prior knowledge in mathematics. | What do you notice in the picture that makes you think of math? Do you know how many cookies there are? How do you know? |
| The student faces challenges when trying to articulate their observations using mathematical vocabulary. | Could the number of cookies be represented by repeated addition? Could this repeated addition be represented by multiplication? On the bottom baking sheet, how many rows of cookies are there? How many cookies are in each row? |
Active Learning (Explore)
Duration: approximately 100 minutes
Assessment can be carried out through…
Introduce students to the situation below and the code:
At the bakery, Maxime has to plan where to put the pastries on the baking sheets before baking them. The machine that places the pastries on a baking sheet uses block coding software. Maxime creates the code below to put 24 pastries on a baking sheet.
Example of Maxime's Code:
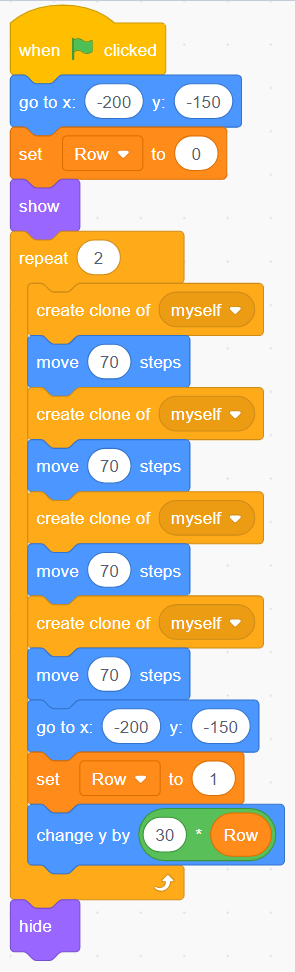image Blocks of code:6 attached blocks:Events block stating, “starts on green flag when clicked”.Motions blocks stating, “go to x-200 y –150’’. Variables block stating ‘’set row to zero’’. Looks blocks stating ‘’show’’. Events block stating ‘’repeat six”. Inside are 11 nested blocks. Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “go to x: ‘-200’ y” ‘-150’”. Variables block stating “change row by ‘1’.Motions block stating “change y by ‘30’ motions block ‘row’”Looks block stating ‘hide’.
Sample questions:
- What do you notice?
- What is Maxime trying to do with this code? (Put 24 pastries on a baking sheet)
- How many pastries do you think will be on the baking sheet? (There will be 8 pastries on the baking sheet.)
- Which block of code "puts" a pastry on the baking sheet? How many times does it occur in the code?
The block "create a clone of myself" puts the pastry on the baking sheet. This block is present 4 times, but in a loop of 2 repetitions, so \(2 \times 4 = 8 \).
- What questions do you have?
- Tell me, in your own words, what this code says?
Invite students to create a pseudocode that represents Maxime's code so that they can predict what will happen when the code is executed. Then ask them if Maxime's code will produce the desired result.
Sample reflections:
- I notice a loop, which means that a series of blocks is repeated.
- I notice that variable blocks are used. I have never used variables.
- I think that 8 objects will be created because the loop repeats 2 times. In the loop, there is the event "make a clone" which repeats 4 times, \(2 \times 4 = 8 \).
- I wonder how I will create a variable.
Example of possible pseudocode:
|
Go to the starting position. |
|
Set the "row" variable to zero. |
|
Show the object. |
|
Repeat 2 times. |
|
Advance 70 steps Make a copy of the sprite. |
|
Advance 70 steps Make a copy of the sprite. |
|
Advance 70 steps Make a copy of the sprite. |
|
Advance 70 steps Make a copy of the sprite. |
|
Return to the starting position. |
|
Add 1 to the row variable, so go up by 1. |
|
Add 30 × (value of "row"), so 30 × 1*. |
|
Hide the object. |
* This part of the code moves the sprite to the beginning of the right row. In this case, each row is 30 pixels apart. So the first row (row = 0) starts at the starting position, the second row (row = 1) starts at the starting position + 30, the third row (row = 2) starts at the starting position + 60, etc.
Note: Some students may notice that the part "Go 70 steps forward, make a copy of the sprite " is repeated 4 times, and they may ask if it would be possible to use a loop to simplify the code. It is in fact possible. This kind of structure is developed more in grade 4 (nested events). That being said, here is what the code with this structure might look like, in case that is one of the avenues of questioning by students.
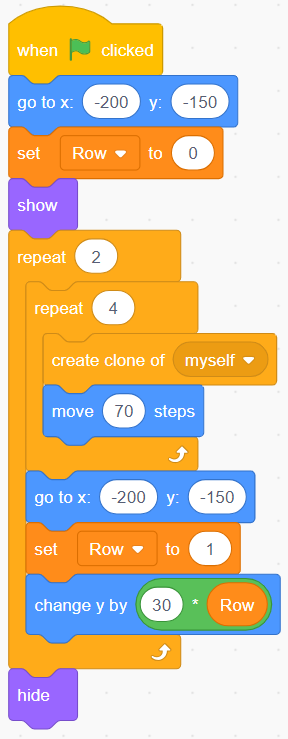image Blocks of code:Events block stating “start on when green flag is clicked”.Motions block stating “go to x: ‘-200’ y: ‘-150'.Variable block stating “set row to ‘0’.”Looks block stating “show”.Control block stating “repeat 2”. Inside are 4 nested blocks.Control block stating “repeat 4”.Inside are 3 nested blocks. Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Motion blocks stating “go to x ‘-200’ y: ‘-150’.”Variable blocks stating “change row by ‘1’.”Motions block stating “changing y ‘30’ variable block ‘row’.”Looks block stating “hide”.
- Ask students to recreate the code using the chosen software.
- Invite students to modify Maxime's code to include 24 pastries, as originally intended.
Note: This will be a good opportunity to try out different functions and model the trial and error approach by applying the process of elimination or systematic testing. Encourage students to save the code as soon as it is functional and make a copy of it from which they can try out different functions or see the effect of changing a block. This way, the student can always go back to the working code (so the risk of errors is very low, which will encourage experimentation).
Possible answer:
This code puts 8 cookies on the baking sheet (2 repeats of 4 cookies). I know that each additional repetition will add 4 cookies to the baking sheet. So I can do a repeated addition of 4 until I reach 24 cookies.
So, 4 + 4 + 4 + 4 + 4 + 4 = 24, so I need to modify the loop to have 6 repetitions (6 × 4 = 24).
Sample code:
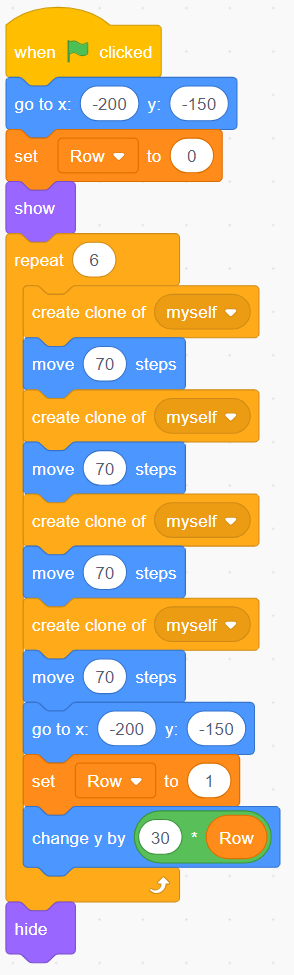image Blocks of code:Events block stating “start on when green flag is clicked”.Motions block stating “go to x: ‘-200’ y: ‘-150'.Variable block stating “set row to ‘0’.”Looks block stating “show”.Control block stating “repeat 12”. Inside are 3 nested blocks. Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Motion blocks stating “go to x ‘-200’ y: ‘-150’.”Variable blocks stating “change row by ‘1’.”Motions block stating “changing y ‘30’ variable block ‘row’.”Looks block stating “hide”.
Ask students to circulate around the classroom to see the codes of other students. Did all students choose to make the same change? Does the result remain the same?
Examples of possible codes (always for 24 cookies):
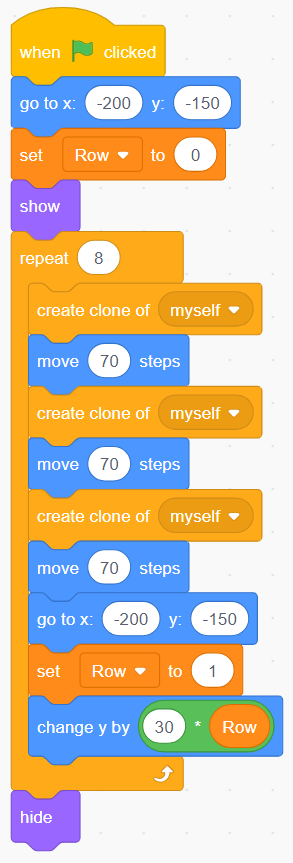image Blocks of code:Events block stating “start on when green flag is clicked”.Motions block stating “go to x: ‘-200’ y: ‘-150'.Variable block stating “set row to ‘0’.”Looks block stating “show”.Control block stating “repeat 12”. Inside are 3 nested blocks. Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Motion blocks stating “go to x ‘-200’ y: ‘-150’.”Variable blocks stating “change row by ‘1’.”Motions block stating “changing y ‘30’ variable block ‘row’.”Looks block stating “hide”.
Represents 12 × 2 = 24
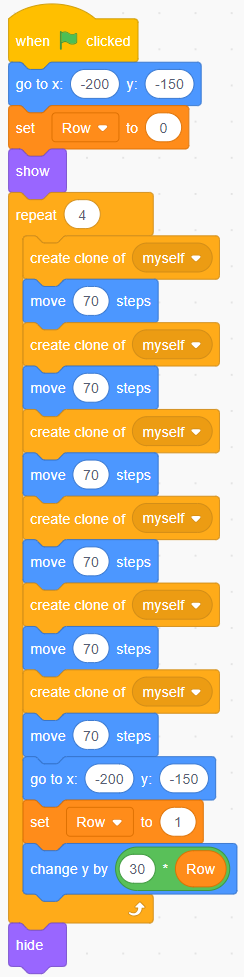image Blocks of code:6 attached blocks:Events block stating, “starts on green flag when clicked”.Motions blocks stating, “go to x-200 y –150’’. Variables block stating ‘’set row to zero’’. Looks blocks stating ‘’show’’. Events block stating ‘’repeat six”. Inside are 11 nested blocks. Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “go to x: ‘-200’ y” ‘-150’”. Variables block stating “change row by ‘1’.Motions block stating “change y by ‘30’ motions block ‘row’”Looks block stating ‘hide’.
Represents 4 × 6 = 24
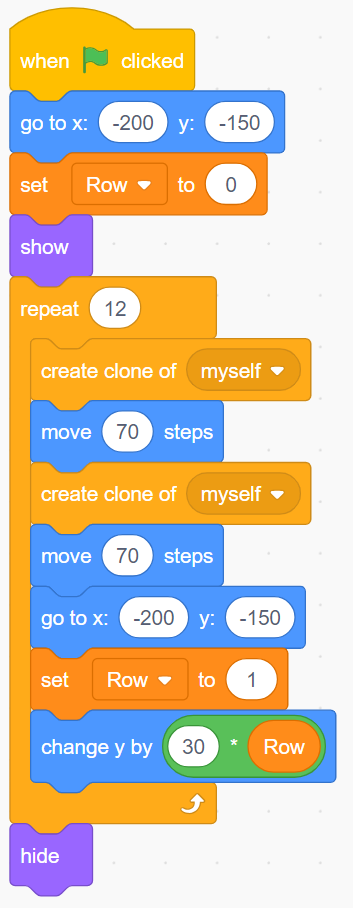image Blocks of code:6 attached blocks:Events block stating, “starts on green flag when clicked”.Motions blocks stating, “go to x-200 y –150’’. Variables block stating ‘’set row to zero’’. Looks blocks stating ‘’show’’. Events block stating ‘’repeat six”. Inside are 11 nested blocks. Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “create clone of myself’’.Motions block stating “move ‘70’ steps”.Controls block stating “go to x: ‘-200’ y” ‘-150’”. Variables block stating “change row by ‘1’.Motions block stating “change y by ‘30’ motions block ‘row’”Looks block stating ‘hide’.
Represents 8 × 3 = 24
Sample reflections:
- No, the other students' codes are different. I chose to do 6 rows of 4 pastries, but I also saw 8 rows of 3 pastries and 4 rows of 6 pastries.
- There are several multiplications that make 24, but I think 4 rows of 6 baked goods is the best multiplication to make good use of the space.
- The results are the same, there are always 24 pastries on the baking sheet.
- The results are different, even though there are still 24 pastries on the baking sheet, because the arrangement of the pastries is different.
- Have students create a code for today's orders.
- 20 cranberry scones
- 81 raisin cookies
- 47 raspberry turnovers
- Ask students questions to find out if they have the same representations as the other students.
Possible Answers
20 cranberry scones:
- I used 2 × 10 multiplication and Valerie used 4 × 5 multiplication.
- I think the 2×10 array is not as effective as the 4×5, since you waste a lot of space on the baking sheet.
- I notice that there are several ways to represent 20 cookies using the array: 4 × 5, 5 × 4, 2 × 10, and 10 × 2.
81 raisin cookies:
- There is just one way to represent this number, since there is just one multiplication that has a product of 81, or 9 × 9.
Note: Multiplication facts up to 10 × 10 are prioritized in this learning situation. However, 3 × 27 or 27 × 3 may be accepted if offered.
- I notice that the pastries form a square.
47 raspberry turnovers:
There are no two numbers that, when multiplied, add up to 47, but I know that 9 × 5 = 45. I can first create a code to put 45 turnovers on the baking sheet (9 rows of 5 turnovers) and then add two more on the side.
Sample code:
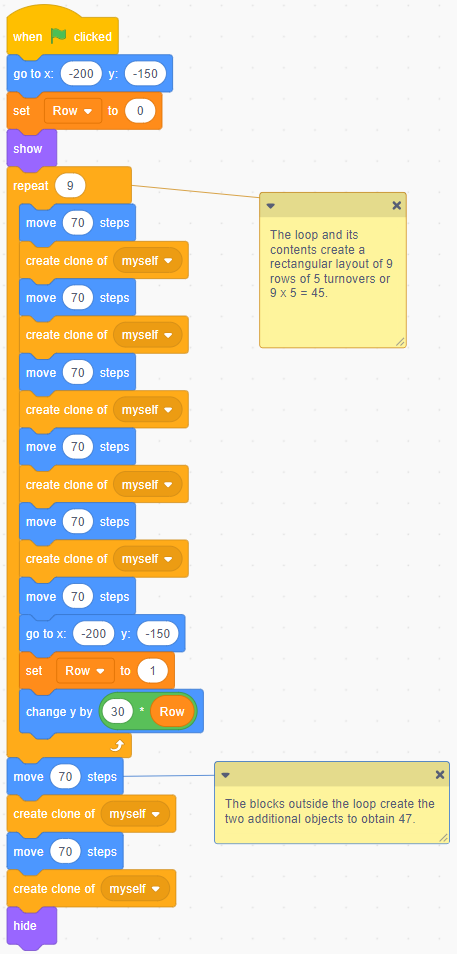image Blocks of code:Events block stating “start on when green flag is clicked”.Motions block stating “go to x: ‘-200’ y: ‘-150'.Variable block stating “set row to ‘0’.”Looks block stating “show”.Control block stating “repeat 9”. Inside are 11 nested blocks.Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Motion blocks stating “go to x ‘-200’ y: ‘-150’.”Variable blocks stating “change row by ‘1’.”Motions block stating “changing y ‘30’ variable block ‘row’.”Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Controls block stating ”create clone of myself.Motion blocks stating “move ‘70’ steps.”Looks block stating “hide”.Two Comments stating:- The loop and its contents create an array of 9 rows of 9 socks or 9 x 5 = 45- The code blocks on the outside of the loop create the two extra objects in order to obtain 47.
Note: This same reasoning could be used with other numerical facts, such as 6 × 7 = 42, and 5 more make 47.
| Possible Observations | Possible Interventions |
|---|---|
| The student fails to use the loop correctly. | Use different approaches to explain the structure. The loop, for example, looks like a mouth, and everything in the mouth is chewed a certain number of times. Ask the student if the loop contains all the elements that will need to be repeated (sometimes there are omissions, especially towards the end of the loop). Ask the student to name the multiplication that is being represented with the code. Where can you find the two multiplied numbers in your code? Provide materials for the student to "do the robot" in an unplugged coding activity by following the code as indicated; for example, one token = one pastry to be placed on a rectangular baking sheet. The student can then translate their actions into code for the computer. |
| The student does not change the moves, so not all the baked goods go on the baking sheet or fill it. | Ask the student to start their code, then ask them about what they observe. Ask the student if they used the surface effectively. Ask the student if it is possible to see all the pastries on the baking sheet. Review with the student, in the context of coding, the following terminology: advance, go to, and add |
| The student forgets to hide the object at the end of the code. Example:  |
Ask the student to count the number of pastries on the baking sheet. Ask the student to explain what they need to do to solve the problem before looking for the appropriate block. Note: There are several solutions to this problem; for example, the student could add a block at the end of the code that returns the sprite to its original location, which creates the same visual result as "hiding" the sprite. |
| The student forgets the "create a clone of myself" block. | Ask the student if they can count the baked goods after starting the code. Ask the student to explain what they need to do to solve the problem before looking for a block. Note: There is also a block called "stamp" that can produce a similar effect. |
Consolidation (Learning)
Duration: 15 minutes
Assessment can be carried out through…
Select a few students from the class and ask them to present or explain their code (using a pseudo code). During this discussion, ask the other students in the class to point out similarities and differences between the codes.
Review the effective use of loops in a code.
Consolidation of Learning
Have students create code to represent regular geometric shapes. If the coding software used has an option to draw lines (for example, the "pen" in Scratch), students can draw shapes using sprite moves and rotations. Loops will reduce the amount of code to achieve a goal.
To code a square trajectory, for example, you need to know the properties of a square (4 right angles and 4 congruent sides). The code for the trajectory could therefore look like this:
Adding loops can reduce the code to this:
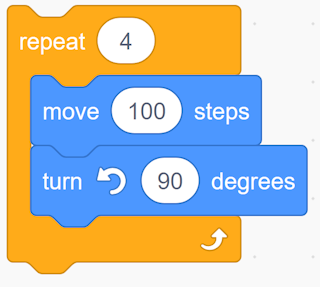
Students can apply this same process to create code for rectangles.
Links to other mathematical domains (repetitive events)
Number
B2.6 Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays. Using a loop, students can make the connection between repeated addition and multiplication. By coding moves and reproductions of sprites, the student can move from a representation of groups of objects to the array.
Algebra
C1.1 Identify and describe repeating elements and operations in a variety of patterns, including patterns found in real-life contexts. Code sequences found within a loop represent the pattern of a repeating pattern sequence. Therefore, students can use pseudocode to describe the action inside the loop.
Spatial Sense
E2.8 Use appropriate non-standard units to measure area, and explain the effect that gaps and overlaps have on accuracy. By using repetitive events to make a multiplication represented in an array, the student can make the connection between the number of objects arranged in a rectangle and the area.
Differentiated Instruction and Universal Design for Learning
- Give the disconnected blocks to the students to replace in order to reproduce the code.
- Give students a pseudo code to use as a map.
- Offer students a basic code so that they can simply go and modify it according to the number of pastries they want.
- This code also lends itself well to nested events, a slightly more complex structure, but one that can make the code easier to interpret. Some students who are more comfortable with the code will be able to use this structure by putting loops inside loops.
- For students who would benefit from a challenge, it would be possible to add some parameters, for example, a maximum number of baked goods that can go on a baking sheet, which creates a more complex mathematical situation to represent using the code.