C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in patterns that have repeating elements, movements, or operations.
Skill: Determining and Using Rules to Extend Patterns
Understanding Change
Students live in a changing world. Understanding that change is a part of life and that most things change over time (e.g., each year during the growing season, height grows, weight increases, feet get longer) is a final component of developing algebraic thinking. Observed changes can be described qualitatively (e.g., I am taller than last year, my hair is longer, the bucket filled with water quickly during the storm, it is colder than this morning) and quantitatively (e.g., I grew 2 cm this year, the bucket of water filled with 50 ml in 30 minutes, the temperature dropped 6°C in three hours). Students need to learn to observe and understand changes in patterns.
Change and patterns are two concepts that cannot be separated in the study of patterns. Students realize that a change in one term affects the next term. Subsequently, observing changes and relationships between those changes allows them to predict other terms in the pattern and thus generalize. By observing the growing pattern below, students can extend it and find the rule. Students can describe the rule by explaining the addition of a row of squares at the base and a column to the right of the existing square.
Growing Patterns
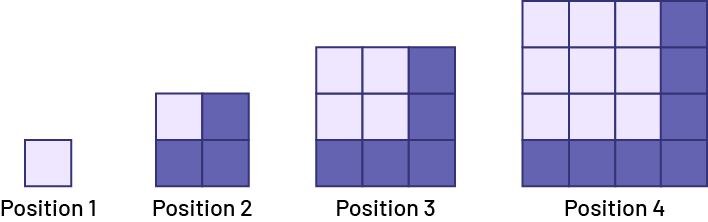
By examining the change from one term to the next, students observe a rule that allows them to predict the number of unit squares making up the shape in the next term. Students can build a table of values to organize the data to better see the change and find the rule.
Table of Values
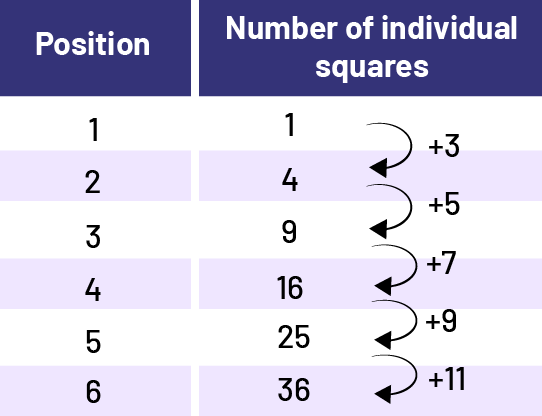
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 21-22.
Relationships Between Terms
Using a variety of representations and materials, students explore the concept of pattern in non-numeric and number patterns, and communicate, in their own words or through personal representations, their observations and perceptions of the relationships among the terms in the pattern.
In the primary grades, students learn to recognize the relationships that exist between terms in a pattern. By examining and exploring patterns, they identify how this information can be used to determine what needs to be added to a pattern to extend it. By discovering relationships, students realize that the next terms in the pattern are not chosen randomly. Finding patterns is, in itself, an important problem-solving strategy.
Students continually redefine their mental image of patterns. Their representation is often limited by the examples they are presented with or by their personal experiences. It is therefore important that teachers present a variety of representations and rules in activities to facilitate the integration of the concept. The key is to develop students' algebraic reasoning by enabling them to justify the extension of a non-numeric or number patterns and by explaining the relationships between the terms of the pattern.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 27.
Non-Numeric Patterns
In order to extend a pattern, students must indicate the elements of the pattern and their order. By extending a pattern and justifying their choice, students communicate their understanding of what the rule is. For example, a student may say, "I'm going to be the sailboat because right before me is the balloon and the continuation is always sailboat, balloon, sailboat, balloon… repeating."
With their bodies or manipulatives, students can explore the extension of a pattern and make changes with greater ease. Students can also extend a pattern constructed by others.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 38.
Number Patterns
Very early on, children become aware of pattern rules in their environment, in nature, in the objects that surround them. This is why it is possible to introduce number patterns as early as the first year. At the same time, students develop their sense of number, can count in intervals and backwards, and later on, appropriate the concept of addition as a grouping of objects. All of these concepts have an important connection to learning number patterns.
As students begin to explore the base-10 numbering system, which is synonymous with the decimal system, they discover that the digits 0-9 are repeated when they count beyond 9 (10, 11, 12, 13, 14, 15 ). Seeing and justifying this pattern in the decimal system enhances understanding of number sense and groupings (units, tens, hundreds, etc.). For example, when counting by 2, starting at 16, students observe a predictable pattern in the numbers 16, 18, 20, 22, 24, 26, 28, 30, 32. This is a first step toward exploring multiples of 2. This understanding also leads to an ability to count from any number by any skip.
Similarly, when students count by 5s, they quickly recognize a pattern, i.e., that the units alternate between 0 and 5 (5, 10, 15, 20…). Students can generalize this discovery informally by saying that any number that is a multiple of 5 will end with the digit 5 or 0.
It may be helpful for teachers to suggest that students identify patterns in a number grid to help them develop conceptual understanding of number and the base-10 number system.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 49-50.
Skill: Making Predictions and Justifying Them
The use of concrete and semi-concrete materials, a variety of representations and rules allows students to make and justify near and far predictions.
Making a close prediction is to indicate or represent what the next terms in a given pattern will look like. The prediction can be verified simply by extending the pattern.
Making a far prediction is to indicate or represent what a pattern will look like far beyond a given section. Calculations are often required to make a correct prediction or to check its plausibility.
Source : Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Students can best describe a pattern when they understand the relationship between each term in the pattern and the position each term occupies in the pattern. They can do this by numbering each term in the pattern in turn.
In this way, students can refer to certain terms in the pattern (e.g., in this pattern, the suns are in the 3rd, 6th , and 9th positions from the left). By analyzing the relationship between the position and the term, students can easily predict the position of the next terms in the pattern, without having to extend it. This analysis allows them to generalize (e.g., a sun will be in the 12th position since it is in the 3rd position of each pattern. The position of the sun is always a multiple of 3).
In the problem situation "How many suns will there be in the pattern of 10 patterns?", elementary students can informally discuss, model, create multiple representations, describe them, and conclude by finding the number of suns and justifying their approach. Exploring this type of problem allows students to develop their algebraic thinking and serves as a foundation for using a rule and variables in future grades.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 38-39.
In growing patterns, there is also a relationship between the position of each shape and the number of elements in each shape. This relationship is a very important mathematical concept, which leads to a more formal generalization, the pattern rule formulation.
For example, by carefully analyzing a pattern, students see that the shape in the 1st term has two geometric shapes, the shape in the 2nd term has four, the shape in the 3rd term has six, etc. Students see that there are always twice as many geometric shapes as the positionof the shape. This observation, the functional pattern rule, allows them to find any term in the pattern without having to extend it.
Informal discussions dealing with the relationship between term and the number of elements that make up the term can occur in determining the pattern rule and extending the pattern.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 45-46.
Skill: Finding Missing Elements in Patterns
In non-numeric and numeric patterns, students need to determine what is in a predetermined position (before, after, or within the pattern). Therefore, they need to determine the pattern rule and then identify the missing shape or number.
Example
Find the term in the 4th term of the following growing patterns.
image pattern with growing patterns. Rank one has 5 red vertical cubes and 2 blue cubes below. Rank 2 has 5 red cubes vertical and 4 blue cubes below. Rank 3 has 5 red cubes vertical and 6 blue cubes below. Rank four is empty. Rank 5 has 5 red vertical cubes and 10 blue cubes below.
Source : En avant, les maths!, 3e année, CM, Algèbre, p. 4.
The study of patterns in a number pattern can continue with a number grid or number line with missing numbers. Students must first find the pattern rule in order to discover the missing numbers, and then explain the addition or subtraction pattern rule. Students can use a calculator to solve this type of problem.
Examples
Missing Numbers in a Partial Number Grid
Missing Numbers on an Open Number Line
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 67.
Knowledge: Pattern Rules
Recursive Relationship : a rule that allows a patttern to be extended with respect to the difference between terms (also called a constant jump).
Functional Relationship : a rule that extends a pattern by establishing the relationship between the term number and its term.
Source :Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.