C2.3 Identify and use equivalent relationships for whole numbers up to 1000, in various contexts.
Skill: Determining and Using Equivalence Relationships Involving Numbers Up To 1000
In a mathematics class aimed at developing students' algebraic thinking, the traditional teaching objective (learning to calculate) is not omitted; it is largely superseded.
Developing algebraic thinking is a complex process that relies on three fundamental processes: abstracting, generalizing, and operating on the variable.
Note: Although the properties of operations (e.g., commutativity) are explored in the Numbers domain, the process of coming to understand and generalize them falls under algebraic thinking.
Generalize
It is to draw valid conclusions, true in all cases, from the observation and analysis of a few examples (Squalli, 2002, p. 9, adapted citation)
In a situation of equality, students can more easily formulate a generalization when it follows a process of proposition and verification of a conjecture.
A conjecture is the expression of an idea that is perceived to be true in any similar situation.
When students see a recursive phenomenon while exploring various equality situations, they are able to propose a conjecture; for example, they might say that if you add the number 0 to any number, the initial quantity does not change.
Students should then check whether their conjecture is valid in other similar situations. For example, in the situation in the previous example, they could check it with various numbers as well as with concrete materials.
When a conjecture seems to apply to all similar situations, students formulate a generalization in words or using symbols.
Example 1
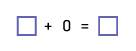
There are three important steps in the generalization process.
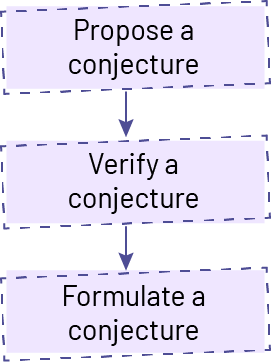
In the primary and junior divisions, conjectures are usually expressed in words by students. They may also be represented by concrete or semi-concrete materials to illustrate their mathematical reasoning as clearly as possible.
Teachers need to expose students to a variety of problem situations that challenge them to practice the skill of making and testing a conjecture; for example, they present the number sentence (50 + 6 - 6 = 50) and ask them what they notice. Then, they offer them the following conjecture: "I wonder, when you add and subtract the same number in a math sentence, if it is the same as when you add or subtract zero." Teachers then invite students to discuss this conjecture with each other and determine if it is still true.
Students test this conjecture with other number sentences. They may not be convinced that it applies to any number sentence or to all numbers, especially large numbers. In the course of the discussion, they can propose their own conjectures as illustrated below.
image Two students negotiate their mathematical reasoning. Student one says ‘’ The mathematical equation 100, plus, 5, minus, 5, equals, 100 is true because if we subtract a number from itself, it is like if we have never added it. Therefore, the phrase becomes 100, equals100. ‘'Student two Says’ ‘I believe that the mathematical equation is true because subtracting a number from itself is equivalent to adding a zero. The quantity does not change. Therefore, the equation becomes 100, plus, zero, equals, 100.’’
After a check of various number sentences, students can conclude that the conjecture is true and formulate a generalization.
Example 2
Since students' vocabulary in elementary school is not yet very developed and precise, initial conjectures usually need to be rephrased or clarified. Ideally, therefore, the formulation of a conjecture should be practiced in a class setting, as shown in the example below. During the discussion, students can point out the limitations of a peer's conjecture and contribute to the formulation of a clearer and more relevant common conjecture. However, it is important for teachers to establish a learning environment in which students perceive each other's questions as positive interactions that can fuel the exchange.
Example 3
The teacher presents the number sentence 564 + 0 = 564 and ask students if it is true or false.
Student: "It is true."
Teacher Staff: "How can you tell?"
Student: "When a zero is added to a number, it doesn't actually add anything, so we get the starting number."
The teacher presents other similar number sentences. After several such exchanges, the teacher then asks students to formulate a conjecture. Student: "All numbers added with a zero remain the same. "
Another student presents a counterexample: "No, because 100 + 300 = 400. The numbers 100 and 300 have zeros in them. Added together, they do not stay the same."
After more discussion, a student makes another guess: Student: "When you add a zero to another number, you get the other number."
Other student: "That's not true."
Teacher: "So you are referring to the number that is right next to a zero?"
Student: "No, added to another number."
After much discussion, the following formulation is adopted: "Zero, when added to another number, is equal to that number." When students see that this conjecture applies to all numbers, they can generalize.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 8-11.
When numbers are decomposed, the parts are equivalent in turn.
Notes
- The principle of equivalence is used to verify many mathematical concepts such as the properties of operations.
- The commutative property of addition and multiplication is an example of an equivalence relation.
- Commutative property and associativity allow students to see the equality of a number sentence and show their understanding of these properties and to see the equality of a number sentence without performing calculations.
Students are not expected to be able to name or define these properties, but they should use them appropriately.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Skills Related to Situations of Equivalence
In the primary grades, students develop the ability to recognize, explain, create, restore, and maintain equivalence through the application of strategies and models such as 10 frames and the number line. These skills are to be developed each grade using progressively larger numbers, consistent with curriculum requirements.
At first, situations of equality and inequality are explored primarily orally and with the help of concrete materials. Later, students are gradually introduced to symbolic representation. However, the use of concrete materials remains just as important and must be used in conjunction with the more abstract representations.
Skill: Recognizing a Situation of Equivalence
"The effective use of concrete materials promotes the learning of algebraic concepts for students at all levels. […]. Since this strategy engages the senses, including touch, sight, and hearing, it gives them the opportunity to transition from concrete to semi-concrete to semi-abstract to abstract."
(Conseil des écoles catholiques de langue française du Centre-Est, 2003, p. 6)
In a problem-solving approach, the use of concrete and semi-concrete materials, as well as models, allows students to recognize and represent situations of equality and inequality.
Examples
It is only after having manipulated various models several times with the same goal, i.e., to recognize a situation of equality or inequality, that students will be able to approach the purely symbolic representation (the number sentence) of this situation. Furthermore, to determine the nature of the relationship between quantities, they must understand that the elements on either side of the = sign are data to be analyzed and not just expressions to be calculated.
Example 1
Exploring the property of commutativity allows students to see the equality of the number sentence 43 + 24 = 24 + 43. Through interventions, teachers encourage students to observe that the same numbers are on either side of the equal sign and that the addition terms are simply switched.
Example 2
The strategy cancel terms or equal expressions allows students to see the equality of a number sentence. Canceling terms involves crossing out the identical terms that appear on either side of the = sign. Crossing out or canceling terms that are on either side of the = sign makes it easier to establish relationships between the remaining terms and helps students develop their algebraic reasoning. This should be shown with concrete materials and not just explained as a rule or procedure.
Skill: Explaining a Situation of Equality
"Students need to discuss what is equal/unequal, same/different, more than/less than, in balance/out of balance. It is through authentic dialogue that students construct the meaning of the concept of equality."
(Taylor-Cox, 2003, p. 17)
To develop their ability to explain a situation of equality, students must go through different stages. The transfer from concrete to symbolic representation is easier when the equality relationship is constructed by following the different steps below.
1. Explore using concrete or semi-concrete materials
Using toys, a student demonstrates the following situation: adding 0 toys to 10 toys.
2. Describe with words and materials
"If I add 0 toys to 10 toys, the quantity will not change since I am not adding anything. It will still equal 10 toys."
3. Represent using symbols
The student can then express this equality symbolically by writing the number sentence 10 + 0 = 10.
4. Propose a conjecture
By exploring several similar situations, the student can assume that adding 0 never changes the quantity.
5. Generalize to all numbers
Appropriate questions in other similar situations lead the student to generalize that adding 0 to any quantity does not change the quantity.
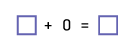
Students also develop their ability to explain a situation of equality by using models. Indeed, the use of models allows students to communicate their reasoning effectively.
Example
To explain the expression 27 + 5 - 5 = 27, students can use an open number line to support their reasoning: "I take a leap of 27 and add a leap of 5. I take another leap of 5 in the other direction, so I am back to 27. It's like I never added a leap of 5."
Ability to Create a Situation of Equality
To get students to achieve equality, it is important to initially present them with a situation in which concrete materials are used. Ask them to represent it with a number sentence, compare the different expressions proposed by the other students and determine if they are all true.
Examples
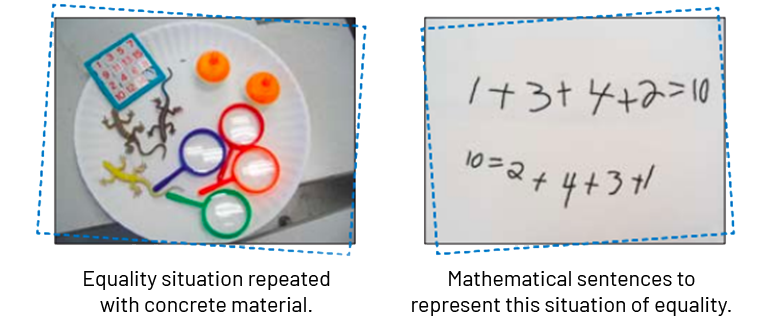image 2 images that represent a situation with equal parts. Image one shows an equal situation represented by concrete materials: 3 lizards, 4 loops, two balls, and one game. The second picture show an equal situation by making an equation: one, plus, 3, plus, 4, plus, two, equals, ten. Ten, equals, two, plus, 4, plus, 3, plus, one.
Afterwards, students can create their own equality situation. Teachers suggest that they write number sentences and represent them using concrete materials. Students should have the opportunity to create equality situations represented by number sentences with larger numbers so that they use the properties of operations or strategies instead of calculations.
Skill: Maintaining a Level Playing Field
By comparing quantities using concrete materials, students explore equivalence situations. To encourage them to extend their reasoning, teachers can ask them the following question in the context of a problem with linking cubes:
- If two towers of six cubes are formed and I add one to one of the towers, what will you do to keep the towers equal?
Through exploration and manipulation, students will see that the same amount must necessarily be added to the other tower to maintain equality. The same process can be followed with two ten frames or with the pan balance.
Later, when students are trying to maintain the equality of a situation represented by a number sentence, it is important to ask them if a number added to or removed from one side of the = sign changes the equality relationship between the two expressions, and if so, why is this so?
Here again, exploration (adding or removing numbers) allows them to conclude that equality is maintained:
- if the number added or removed from one of the two sides of the = sign is 0;
19 + 33 + 0 = 35 + 17
- or if the same number is added or removed on both sides of the = sign.
19 + 33 - 11 = 35 + 17 - 11
Learning to maintain equality is just as important as learning to restore it. It is through frequent concrete exploration of these two skills that students will more easily manipulate the abstract terms in algebraic expressions. For students, acquiring the various skills related to the relationships of equality and, therefore, inequality, serves as the foundation for developing algebraic thinking and learning more symbolic and complex concepts.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 39-48.
Knowledge: Equivalent Relationships
A relationship that compares quantities to show that they have the same value.
Example
352 is equivalent to 350 and 2.
Source : En avant les maths!, 3e année, CM, Algèbre.
Examples
- Represent a number in different ways using rods.
- Represent a number in different ways with base 10 materials.
- Represent a number in different ways with a Rekenrek.
Knowledge: Equality
Relationship between two equal quantities.
Knowledge: Number Sentence
Symbolic representation of a relation. In a number sentence, there is no variable.
Example
True (equal) sentences 75 + 5 = 5 + 75 or 50 = 20 + 20 + 10
False sentences (unequal) 100 = 95 - 5 or 45 + 10 = 15 + 45
Knowledge: Equation
Equality relationship that has one or more variables.
Example
20 + 44 = ____ + 20
a + b = 10