C2.2 Determine whether given sets of addition, subtraction, multiplication, and division expressions are equivalent or not.
Activity 1: Compare Expressions with Arrays
A array is a set of objects arranged in rows and columns to form a rectangle. Arrays are very useful mathematical models for representing numbers, operations and their properties. They also make it easy to explore and visualize relationships between multiplication facts.
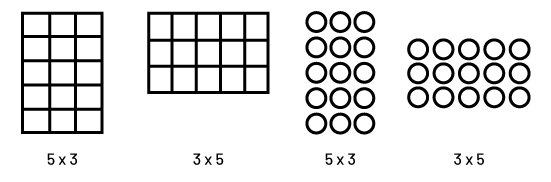
image Geometric motifs and the corresponding equations. The first is a vertical grid of 15 squares. The equation below is 5 times 3. Next is a horizontal grid of 15 squares. The equation below reads 3 times 5. Next is a series of mosaic circles, It is aligned like the first grid but instead of a grid there is a series of circles. The equation reads 5 times 3. Finally, 15 circles in 3 rows placed horizontally. And the corresponding equation reads 3 times 5.
In algebra, arrays are used to show the commutative property of an equality situation.
Introduction to Arrays
Before beginning, prepare concrete, semi-concrete materials that represent an array (e.g., juice box crate, egg carton, chocolate bar, chairs arranged in rows and columns, illustrations). Present the materials to the students and count the rows and columns with them.
Next, observe pictures of arrays (e.g., pictures of boxes filled with juice boxes, chocolate bars grouped in rows, fruit or vegetable displays). Then count the rows and columns in these arrangements. Make the connection to a 10 frame.
Have students design an array with 12 squares on graph paper. Compare the different possible arrangements (4 rows and 3 columns; 3 rows and 4 columns; 2 rows and 6 columns; 6 rows and 2 columns; 1 row and 12 columns; 12 rows and 1 column).
Point out that the shape is always rectangular and that the number of spaces is the same in each row (e.g., 2 spaces in each of 6 rows) and in each column (e.g., 6 spaces in each of 2 columns). Invite students to identify other numbers with which similar arrays can be made.
Activity
Form teams of two and ask them to determine, without using math, whether these two expressions are equivalent using arrays.
Provide each team with large sheets of graph paper and scissors.
8 × 8
For example, students could cut out a array as follows:
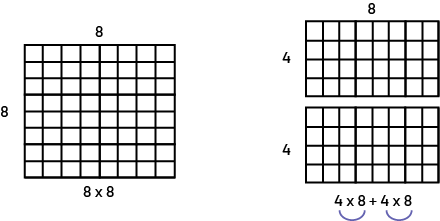image A grid with 64 squares. 8 vertically, and 8 horizontally. An equation below shows 8 times 8. To the right,2 grids. 4 vertically, and 8 horizontally. An equation below shows 4 times 8 plus 4 times 8.
Share with the students by displaying some examples of arrays to show that the two expressions are equivalent since the quantity of squares remains the same if cut in half.
Ask them to find other expressions and illustrate them to show that the strategy works for different expressions.
Example 1
Without calculation, students may already notice that the numerical expression on the left is also represented to the right of the equality symbol, but in two separate parts. Next, ask students to represent number sentences using open arrays.
Example 2
Ask them to find other expressions that represent an equivalence that their peers can prove. The important thing is to discover the relationships that exist on both sides of the equal sign. Students are then able to formulate a conjecture that they verify with other examples.
Example 3
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 73-76.
Activity 2: Compare Expressions with a Balance Scale
Two models of scales are used to explore algebraic concepts: the pan balance and the mathematical scale. With these manipulatives, primary students can verify at a glance and confirm, if necessary, situations of equivalence between quantities. At the same time, they can explore various strategies for representing, maintaining or restoring equality between quantities.
Introducing a Pan Balance
When using objects which have the same mass, the pan balance can promote understanding of the concept of equality in algebra since the relationship between the quantities of objects in each of the pans is concrete and apparent.
Note: Make sure that when students use a balance, they use not only mass to establish balance, but also quantities. Simply comparing the quantities on the pans is not sufficient in algebra. Students need to explore the relationships that exist between these quantities. Some authors advise against the use of the pan balance in primary algebra because students easily confuse the concepts of quantity and mass.
If you use the pan scale, make sure you use objects that all have the same mass (for example, nesting cubes).
Introducing a Number Balance
Introduce the different parts of the number balance using appropriate terms (e.g., lever, fulcrum, tab).
Place two tabs at a number to the left of the lever (for example, at number 3). Ask students to describe the position of the lever.
Ask the following question:
- What must be done to bring the scale into balance?
Share with students to make them realize that:
- the lowered part of the lever represents the higher quantity;
- in this situation, an amount must be added to the right side of the lever to restore the balance;
- the balance is in equilibrium if the quantities are equal on both sides of the lever;
- on each side of the scale, the added quantities can be represented by different numerical expressions such as 2 × 3, 5 + 1, 3 × 2, 1 + 1 + 4.
Introduce this situation to students:
Lucie placed a tab on the 8 on the left side of a math scale and another tab on the 4 on the right side of the scale.
What does she need to do to create an equal situation if she has to perform at least one operation on each side of the scale? Model a possible solution. For example, move the tab on the left side of the scale from 8 to 6 (- 2) and add 2 to the right side.
Ensure that students see that the balance is now in equilibrium and that it now describes a situation of equality.
For each step, write a number sentence:
8 ≠ 4
8 - 2 = 4 + 2
6 = 6
Ask students to repeat the process to find another solution.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 78-79.