C2. Equations and Inequalities
Demonstrate an understanding of variables, expressions, equalities, and inequalities, and apply this understanding in various contexts.
Learning Situation: What Problem?
Duration: approximately 115 minutes
Summary
In this learning situation, students are making connections between situations, and various representations of the situations including equations.
| Overall Expectations | Specific Expectations |
|---|---|
| C2. Equations and Inequalities Demonstrate an understanding of variables, expressions, equalities, and inequalities, and apply this understanding in various contexts. |
C2.2 Solve equations that involve whole numbers up to 50 in various contexts, and verify solutions. C2.3 Solve inequalities that involve addition and subtraction of whole numbers up to 20, and verify and graph the solutions. |
Learning Goals
The purpose of this learning situation is to have students:
- associate an equation with a situation and a corresponding representation;
- to write a situation that corresponds to an equation;
- to represent an equation concretely or semi-concretely.
| Learning Situation | Prerequisites |
|---|---|
| In the primary grades, it is important to introduce students to the concept of equality. Students determine the value of the unknown in a simple equation by referring to the numerical facts of addition and subtraction, and represent a simple equation using concrete materials, semi-concrete materials and symbols. In grade 4, students continue to represent equality in a variety of ways and use these representations to solve simple equations. |
Students have learned to solve problems by performing calculations to obtain an answer. Instead, in this activity, students are asked to develop a situation that represents a given equation, but not solve it. To be able to complete this learning situation, students must:
|
Materials
- Appendix 4.1 - Set of 15 cards (one set of cards per team of three)
- shoebox
- Appendix 4.2 - Photocopied equations on coloured paper or cardboard (one equation per pair)
- manipulatives (for example, cubes, base ten materials, balance scales)
- cardboard or coloured paper
Mathematical Vocabulary
unknown, equality relation, equation, symbol
Before Learning (Warm-Up)
Duration: approximately 45 minutes
Preparation
- Photocopy and cut out the index cards from each of the pages in Appendix 4.1 so that each team of three has a complete set (15 cards).
- Place each set of cards in an envelope. Place all the envelopes in a shoe box.
- Present students with the following situation:
While cleaning out the closet, I found an algebra kit. This kit contains envelopes with 15 index cards in each envelope. On the index cards, there is either an equation, a situation or a pictorial representation of a situation. I need your help to reorganize the contents of each envelope. In teams, you must match each Situation card with its corresponding Equation card and Representation card. Since there are 15 cards in the envelope, you will have five groups of three cards.
- Ensure that the task is understood by asking a few students to explain it in their own words.
- Group students into teams of three. Provide each team with a set of 15 cards. Have students form five groups of three cards (situation, situation representation and equation). Allow students sufficient time to complete the task.
Note: The purpose of the learning situation is to analyze the situation, not to solve a problem. By omitting the question that is usually asked at the end of a situation (for example, How many altogether?), students will be less likely to attempt a calculation, and their algebraic reasoning will be more involved. It is therefore essential not to emphasize the value of the unknown.
- Compare the groupings that the students have made by presenting the situations one at a time.
- Draw out the different groupings by asking students questions such as:
- Why did you put these three cards together?
- How do you know that this grouping is acceptable?
- Why does this representation fit this situation and this equation and not others?
- Are there other possible groupings?
- What types of representations are there?
- Which equation best represents this situation?
- Why does this equation not represent this situation?
- If students have difficulty interpreting the representations of the situations, review with them the elements of different models (for example, the direction of the arrow on the number line to indicate whether it is an addition or a subtraction, the position of the unknown on the scale).
Note: It is possible that some teams may form different groupings from other teams. If a team can justify a grouping, then it is accepted. In Grouping A, for example, the equation that most accurately represents the situation is 
. A team can also present arguments that the equation 
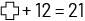is also valid. However, it would be impossible to justify that the equation 
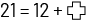is valid, since the given situation involves an addition, not a removal. The equation must represent the situation, not the strategy that could be used to determine the missing data. It is important to note that one equation more closely respects the situation than another, as it follows the direction of time and the action being taken.
- Continue the presentation of the algebra kit by telling students that in addition to the envelopes there are several equation sheets. Show students these equations. Tell them that they will have to complete the kit by creating a Situation sheet and a Representation sheet of the situation corresponding to the equation they will be given. Ensure that the task to be performed is well understood by asking a few students to explain it in their own words.
Active Learning (Exploration)
Duration: approximately 45 minutes
- Group students into teams of two. Provide each team with one of the equations in Appendix 4.2 - Equations. Provide them with manipulatives and scrap paper.
Allow students sufficient time to complete the task. Circulate around the classroom and observe the teams. Encourage students to think about the accuracy of their situation and representation. Ask them questions such as:
- Why did you choose this representation?
- Can you represent this situation differently?
- Does your model represent the equation?
- Is it possible to interpret your model in another way?
- What element of your model allows you to recognize that it represents the equation?
| Possible Observations | Possible Interventions |
|---|---|
| A team does not know how to represent the equation. | Ask students questions such as: In the representations of situations presented earlier, is there one that has a similar equation?
Can you read me the equation and explain it to me in words? |
| One team produces a representation for equation 15 - ◯ = 8 that does not clearly show the shrinkage in the equation. | Ask students questions such as: Is this an add or remove situation? What element can you add to your drawing to clearly indicate the operation being performed? What operation are you representing? How is it represented? |
| Starting with the equation 16 + ◯ = 25, one team adds the value of the unknown in their situation: On the bus, there are 16 occupied benches and 9 empty benches. The bus contains a total of 25 benches. | Ask students questions such as: In the starting equation, can you show me where the 9 is? Why is there an octagon in the equation? Can you change the situation so that the value of the unknown is not disclosed? |
| One team creates a representation for the equation 25 = 12 + 4 + ◯ that does not clearly show the relationship between the quantities on either side of the equal sign. | Ask students questions such as: What do the lines represent in your representation? What could you add to show more clearly the relationship between the animals and the number 25? |
- Distribute large sheets of paper and markers to the teams. Ask the students to write down their situation and their representation. Make it clear that the equation should not be written down. Then ask them to post their work.
- Once all the work has been posted, assign each team the task of coming up with an equation that matches the situation and representation that another team has created, writing it on a card (previously distributed) and attaching it to the bottom of the sheet.
Example
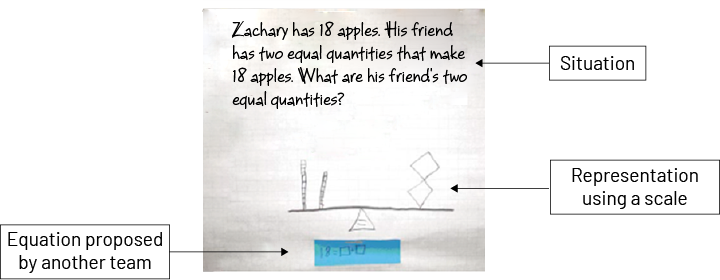Image Drawing of students that were asked to explain a situation. The students then made an equation and represented it with a drawing of a scale. An equation from other students were compared.
Consolidation of Learning
Duration: approximately 25 minutes
- Invite some teams to justify the equation they have proposed. Ask others to explain the situation and the representation they have created and invite them to paste the initial equation on their worksheet so that they can compare it with the one proposed by another team.
Example
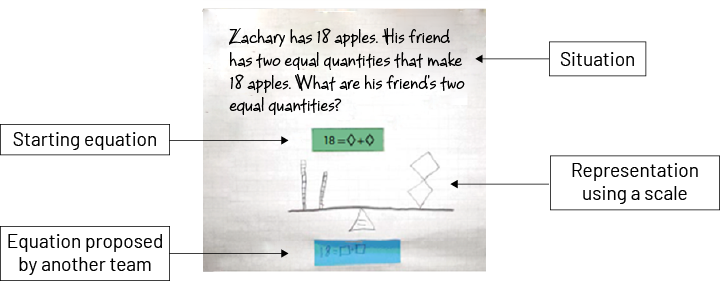Image Drawing of students that were asked to explain a situation. The students then made an equation and represented it with a drawing of a scale. An equation from other students were compared.
- Invite other students to contribute to the discussion and enrich the learning by asking questions and making relevant observations and interventions. Encourage them to use precise vocabulary.
- Assist students, as needed, with questions based on the content of the posted work.
For example:
- How are the numbers in your equation a part of your representation?
- What elements of the representation helped you determine the operation in your equation?
- How can your representation be changed to better represent the proposed situation?
- What would be different in your representation to match your equation? What would change the problem?
- Do you notice any similarities between some of the equations? Which ones?
- How are the equations different?
Here are some possible groupings and student justifications.
Grouping 1
Image Example of regrouping possibility with symbols and numbers. ‘Crescent moon’, plus, 8 equals 15. 15, equals, 8, plus ‘crescent moon’. 8, plus, ‘heart’, equals, 15. 15, minus, ‘cross’, equals 8. 15, minus, 8, equals, ‘cross’.
- The numbers are the same.
- The position of the unknown is different, but its value is the same.
- Three equations represent a sum and two equations represent a difference.
- The symbols are different, but the value of the unknown is the same.
- It is possible to show the commutativity property by comparing the first and third equations.
Grouping 2
Image Example of regrouping possibility with symbols and numbers. 25, equals, 12, plus 4, plus, ‘pentagon’. 12, plus, ‘sun’, plus, 4, equals, 25. 16, plus, oval, equals 25.
- The quantities are the same.
- The position of the unknown is different, but its value is the same.
- The last equation looks like the others, because 12 plus 4 is the same as 16.
Grouping 3
- The two equations represent a sum.
- In the first equation, the symbols are the same, so the value of the unknown should be the same. However, in the second equation, the symbols are different, so their value should be different, but it is possible that their value is the same.
Differentiated Instruction
The activity can be modified to meet the needs of the students.
| To Facilitate the Task | To Enrich the Task |
|---|---|
|
|
);Follow-up at Home
At home, students can create an equation involving addition or subtraction and use familiar objects to represent it concretely.
Example
Created equation: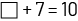 
Possible representation: a cup to represent the unknown and pasta to represent the known quantities.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 123-131.
Students can then represent the equation with an illustration and explain to a family member the relationship between the concrete representation, the semi-concrete representation and the equation. The next day, teachers invite a few students to present their equation and its concrete or semi-concrete representation, and facilitate a discussion with the class.