C2.3 Solve inequalities that involve addition and subtraction of whole numbers up to 20, and verify and graph the solutions.
Activity 1: Solving Inequalities
- Present students with the following scenario:
There are eight horses, two sheep and cows in the pasture. The number of cows and sheep together is smaller than the number of horses. How many cows can there be in the pasture?
Strategy 1
Solve an inequality using a visual representation
I represent the situation using the inequality 2 + v < 8.
I use a visual representation to solve it.
I know that the number of sheep and cows together must be smaller than eight. To find the number of cows, I use the scale model. To keep both sides of the inequality in balance, I have to apply what I do to one side to the other. I then remove the two sheep from the left side. Since I remove two sheep from the left side, I also remove two horses from the right side.
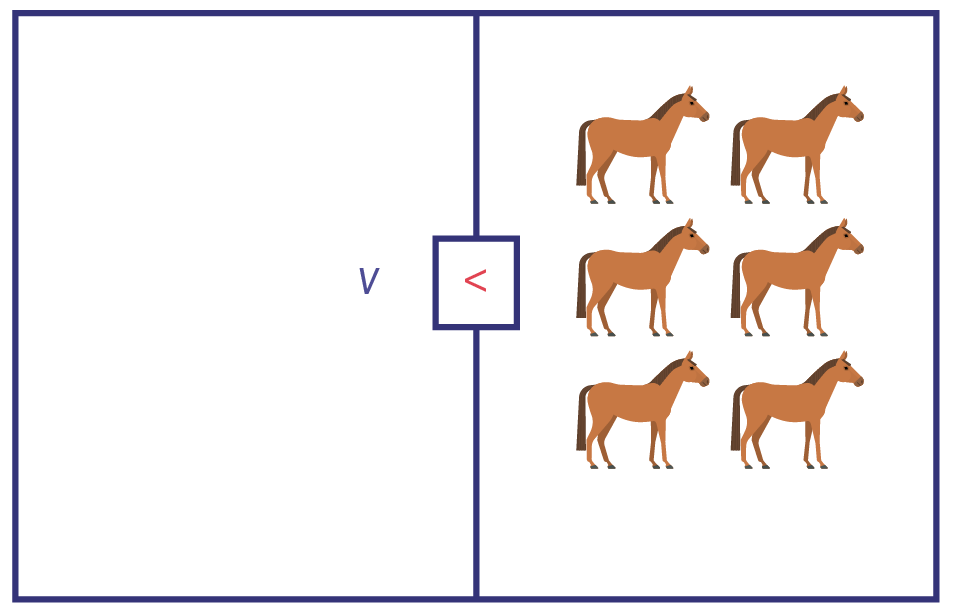
There are six horses left, so v < 6.
Checking my answer:
|
2 + 5 < 8 → 7 < 8 2 + 4 < 8 → 6 < 8 2 + 3 < 8 → 5 < 8 2 + 2 < 8 → 4 < 8 2 + 1 < 8 → 3 < 8 |
In the pasture, there must be less than six cows. So there can be from one to five cows in the pasture, because in the problem it says that there are cows. So I don't write zero cows.
Strategy 2
Solve an inequality using the balance model
I solve the inequality 2 + v < 8 using the balance model.
I need to isolate the variable v, that is, I need to cancel values on both sides of the inequality until v is alone. To neutralize the 2 that is added to v, I must subtract 2 from that same value. To keep the balance on both sides, I have to do the same thing to the 8.
The value of v is smaller than 6.
|
2 - 2 + v < 8 - 2 v < 6 |
To represent the solution on the number line, I placed an empty point on 6. This indicates a strict inequality relationship, which means that the number of cows is less than 6. I placed points on the number line, since the cows are whole. There is not a fraction of a cow in the pasture. I put dots on the numbers 1 through 5, since in the problem it says there are cows. I do not write zero cows.
v < 6
Checking my answer:
|
2 + 5 < 8 → 7 < 8 2 + 4 < 8 → 6 < 8 2 + 3 < 8 → 5 < 8 2 + 2 < 8 → 4 < 8 2 + 1 < 8 → 3 < 8 |
In the pasture, there must be less than six cows. So there can be from one to five cows in the pasture, because in the problem it says that there are cows. So I don't write zero cows.
Source: translated from En avant, les maths!, 4e année, CM, Algèbre, p. 3-5.
Activity 2: Solving a Strict Inequality Relationship
- Present students with the following problem:
Students read in the reading area of the classroom. Four more students join the group. There are now fewer than 10 people in the reading corner. How many students were reading in the reading corner at the beginning?
- Allow students to work in teams to solve the problem.
Example
We represent the problem as an inequality.
The number of students reading in the reading corner is represented by the variable p.
Four more people join the original group, so p + 4.
Less than 10 people read in the classroom reading area, so p + 4 < 10.
To find the number of students who were reading in the reading corner at the beginning, the inequality is:
p + 4 < 10
| p | p + 4 | < 10 |
|---|---|---|
| 0 | 4 | yes |
| 1 | 5 | yes |
| 2 | 6 | yes |
| 3 | 7 | yes |
| 4 | 8 | yes |
| 5 | 9 | yes |
| 6 | 10 | no |
| 7 | 11 | no |
There were students reading in the reading corner of the classroom before the other four students were added. Then it is impossible for there to be zero people or one person, so p = {2, 3, 4, 5}.
At first, there were two, three, four or five students reading in the reading corner.
- Ask a few teams to present their solution. Allow students to review their answer.
Activity 3: Solving a Broad Inequality Relationship
- Present students with the following scenario:
The small corner café can accommodate up to 20 people in its establishment. There are 11 people sitting at the tables. Up to how many more people can the little café seat?
- Ask students to solve the inequality.
Example
We know that the number of people that the little corner café can accommodate is 20 or less, and that there are already 11 people sitting at the tables.
- We solve the inequality 11 + p ≤ 20 using the balance model. To keep both sides of the inequality in balance, we need to apply what we did to one side to the other side. If we remove nine people from the left-hand box, we must also remove the same number of people from the right-hand box.
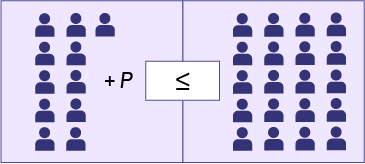Image Image on a balance with number of people on each side. The equation states 11 people on the right side, plus, ‘p’, less then equal to, 20 people on thleft side.
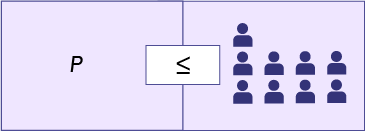Image Image on a balance with number of people on each side. The equation states ‘p’ on the right side, less than or equal to, 9 people on the left time.
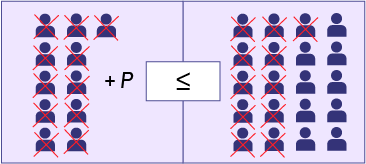Image Image on a balance with number of people on each side. To maintain an equilibrium 11 people are crossed on the right and left side.
- We represent the solution, on the number line, by putting a solid point on 9, since it is a broad inequality relationship. Thus, the number of people that the small café can still accommodate is less than or equal to 9.
We check the answer:
|
11 + 9 ≤ 20 → 20 ≤ 20 11 + 8 ≤ 20 → 19 ≤ 20 11 + 7 ≤ 20 → 18 ≤ 20 11 + 6 ≤ 20 → 17 ≤ 20 11 + 5 ≤ 20 → 16 ≤ 20 11 + 4 ≤ 20 → 15 ≤ 20 11 + 3 ≤ 20 → 14 ≤ 20 11 + 2 ≤ 20 → 13 ≤ 20 11 + 1 ≤ 20 → 12 ≤ 20 |
The small cafe can still accommodate nine people or less.