At a Glance...

Before Learning (Warm-Up)

Approximate time: 60 minutes

Review with students the concept of relation and some of its representations using the following situation.

Ask students the following questions:

• If Dimitri and Anouka rent five movies, how much does it cost them? Why do you think so?
• After renting 17 movies, how much will they have spent? What did you do to determine this amount?

Next, create a table of values with students that represents the relationship between the number of movies rented and cost (the dollar amount spent).

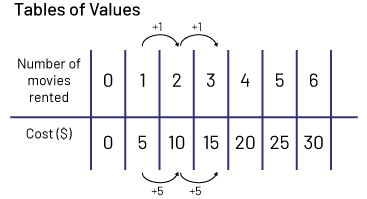
Encourage students to analyze relationships between numbers by asking questions such as:

• If you look at the row labelled "Number of movies rented" in the value table, what do you see? (From one column to the next, there is always one more movie than in the previous column, so the regularity is to add 1 each time; the recursive relationship can be expressed as "+ 1".)
• If you look at the row labeled "Expenses ($)" in the table of values, what do you see? (From one column to the next, there is always $5 more than in the previous column. So the regularity is to add 5 to each term to get the next term and the recursive relationship can be expressed as "+ 5".)
• What relationship do you notice between the number of movies viewed and the cost? (The cost is always five times greater than the number of movies viewed.)

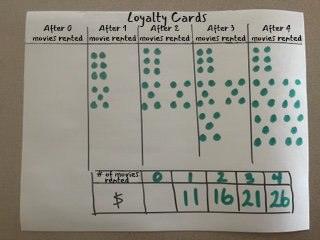
Tell students that the movie rental site offers a virtual loyalty card to its customers. Explain that the card earns one point for every dollar spent.

Show the class the loyalty card of a person who has not yet viewed a movie and those of people who have viewed one, two, three and four movies respectively. The picture below illustrates two examples of sets of loyalty cards representing the amount spent according to the number of films viewed. For example, after viewing a movie for $5, there are five points on the card, after viewing a second movie, there are 10 points on the card and so on.

Note: The non-numeric growing pattern thus created by the loyalty card representations makes it easier to determine the pattern rule. It is important to start the pattern with the representation of this particular loyalty card with no movie rentals because in subsequent learning tasks, some movie rental sites will require a subscription fee before a movie can be rented.

Guide students to verbalize a rule that represents this relationship by asking questions such as:

• How would you describe the loyalty card of a customer who rented 12 movies?
• How much did this customer spend on this movie rental site?
• After renting 20 movies, how much would someone have spent?
• What did you do to determine this amount?
• How could you determine the amount paid quickly, regardless of the number of films rented?

Here is an example of how a student might express the pattern rule in everyday language: "After renting 20 movies, there will be 20 columns of 5, so 100 points on the loyalty card. Each point represents $1 spent. So, we always multiply by 5."

To help this student clarify their thinking and express their pattern rule more clearly, ask questions such as:

• What is multiplied by 5? (The number of movies rented)
• Multiplying the number of movies rented by 5, what do we get? (The amount spent)

The student can then express a more specific rule: "When I multiply the number of movies rented by 5, I get the amount spent."

Explain to students that when describing a quick way to determine the value of any term (e.g., the amount spent) in a pattern, we are expressing a rule defining a functional relationship between the term number and the value of the term in the pattern.

Form teams of two students. Give each team a copy of Appendices 5.1A and 5.1B and read aloud the following situation:

Also read the questions in Appendix 5.1A and ensure that students understand the task at hand.

Note: The advantage for students of starting in Question 1 with a concrete representation of the situation rather than a semi-concrete representation such as a drawing is that they can quickly rearrange the material if they make a mistake rather than having to erase or start over. Most students will have no difficulty representing the pattern of accumulating points on a loyalty card for rented movies, but some will tend to forget to represent the number of points on the loyalty card with no rented movie. Have them recognize that a $4 subscription is required and that they must represent the points on a loyalty card with only that amount (when zero movies have been rented).

Invite teams to complete the task. Observe their work and intervene as needed. Pay particular attention to whether students create a non-numeric growing pattern that shows the regularity clearly.

If necessary, ask questions such as:

• Are the cubes (tokens, stamps…) always added in the same way and in the same order?
• What is similar about the pattern from one card to another?
• What is different from one card to another?
• What is the pattern rule for this pattern?
• How many points are awarded on the loyalty card when no movies are rented? How do you know?

Here are some examples of student work.

• This team represented the amount spent after a movie rental, $9, by a group of four cubes and a group of five cubes. They then added five cubes to each of the subsequent showings. However, they did not place anything under the label "Loyalty card after 0 movies rented".

• This team simply counted out the number of cubes required to represent the amount spent, without regard to their arrangement. The addition of five cubes from one representation to the next cannot be easily identified, making it more difficult to describe the pattern rule that represents the relationship between the number of movies rented and the amount spent.

• This team structures the manipulatives to create a concrete non-numeric pattern. They then produced a semi-concrete non-numeric pattern of loyalty cards using a bingo marker. By creating these two patterns, this team has represented the situation clearly and accurately. It will then be easier to develop a rule to match this situation.

When teams have completed the task (Appendix 5.1A), ask some teams to post their loyalty card patterns. As a class, review the questions, checking the significance of the patterns posted.

Encourage students to compare the two movie rental sites and formulate a pattern rule for each situation by asking questions such as:

• What is the cost of renting five movies at each site? (At the first site, the cost is $25 (5 movies × $5) and at the second site, it is $29, because you have to add the $4 subscription cost)
• What is similar between the two sites? different? (What is similar is the $5 rental fee per movie. What is different is the presence or absence of a $4 subscription fee)
• How can we quickly determine the amount of money spent based on the number of movies rented at each site? (To quickly determine the amount spent at the first site, multiply the number of movies rented by 5, while for the second site, multiply the number of movies rented by 5, then add the $4 subscription fee)

Note: It is important to recognize that a pattern rule may be expressed differently by students depending on their perception of the relationship.

Consolidation

Approximate time: 20 minutes

Invite a few teams to take turns presenting their reports.

Types of presentations

1. Some teams may present their reports with explanations of their approach. Here are some examples of possible student explanations:
• When we received our scenario, we knew that for every movie we rented, there would still be an additional cost because there is a subscription fee.
• Since the rental cost is $6 per movie, we know that for each movie rented, we will have to pay $6 and add six points on the loyalty card.
• At the beginning, we put the dots in any way on the cards, then we realized that it was difficult to see the pattern. So we redid the cards and rearranged the dots to make it easier to see the growing pattern.
• Looking at our pattern of points on the loyalty cards, we can notice the presence of a subscription fee and the addition of six points from one card to the next since, in our scenario, each movie costs $6.

Note: The student supports their explanations by showing the pattern of points on their the loyalty cards.

2. Some teams may report with interpretive questions such as:
• Can anyone tell us how much it costs to rent a movie on this site?
• Among the sites displayed on the board, is there one that presents the same situation as ours? Which one and why?
• Can you tell us if this site requires a subscription? If so, what is the fee?
• Using the pattern visible on the loyalty cards or the table of values, who can tell us what the card would look like after 15 movies rented on this site?
• Can anyone explain, in their own words, a pattern rule that represents the relationship between the number of movies rented and the cost for this site?
3. Other teams may present their report by hiding certain elements, for example, the loyalty card showing 0 rented movies and the term under the 0 in the value table (see photo below). By asking questions, team members lead other students to identify the hidden items and establish the pattern rule that represents the relationship in this scenario.


Encourage students to respond to each presentation and to share their observations or questions. Facilitate the mathematical conversation by asking questions as needed such as:

• When you received your scenario, which representation did you start with (manipulatives, stamps, table of values)?
• Who would be willing to explain in their own words the layout of the points on the loyalty cards just presented?
• Did you use any manipulatives before representing your scenario on your loyalty cards? If so, did it make the task easier?
• These two teams had the same scenario, but their loyalty cards are different. How can we justify that they both represent this scenario?
• Under the scenario just discussed, what would the loyalty card look like after six movies rented? ten movies rented?
• How is the number of points on other loyalty cards determined? What pattern rule represents the relationship?