C3. Apply coding skills to solve problems and create representations of mathematical situations in computational ways, using coding concepts and skills.
Learning Situation: The Probability Machine
Approximate length: 125 minutes
Summary
In this learning situation, the student creates a machine to use the random roll of a die to show that the greater the number of trials, the closer the experimental probability is to the theoretical probability.
| Expectations | Specific Expectations |
| C3. Algebra Solve problems and create representations of mathematical situations computationally using coding concepts and skills. |
C3.1 Solve problems and create representations of mathematical situations computationally by
writing and executing code, including code that includes conditional statements and other control structures.
C3.2 Read and modify given codes, including codes with conditional statements and other control structures, and describe the impact of these changes on the results. |
| D2. Data Describe the probability of events occurring and use this information to make predictions. |
D2.2 Determine and compare theoretical and experimental probabilities of an event occurring. |
| Preferred high-impact mathematics pedagogical practices | Description |
| Learning goals, success criteria and descriptive feedback | Post the assessment criteria in the classroom for students to refer to as they work. Throughout the lesson, take time to circulate among the students and observe what they are doing. Take the opportunity to ask students about their work and give them descriptive feedback on the posted assessment criteria. |
| Mathematical Conversations | In the scenario, students discuss the possible probabilities by rolling the die. As they explore the possible outcomes, they listen to the different opinions and explain their reasoning to their peers. Take time to circulate among the students and ask them about what they notice, what they know or what they would like to know. |
| Flexible Groupings | Students work in groups to foster collaboration. Small group experiments make students feel safe and often motivate them to take risks. They can work in small groups to create their own probability machine that will make the 1,000 throws required easier and more accurate. |
|
Prior Knowledge and Skills |
|---|
|
To be able to complete this learning situation, the student must:
At the end of this learning task, the student will be able to:
|
Success Criteria based on the Achievement Chart Categories
| Skills | Success Criteria |
|---|---|
| Knowledge and understanding |
|
| Thinking skills |
|
| Communications |
|
| Implementation |
|
- block programming software
- dice numbered from 1 to 6
- appendix A (table in which to compile experimental results)
- pencil
Mathematical Vocabulary
Experimental probability, theoretical probability, repeating events, nested events, conditional instruction, control structure.
Situation
Approximate time: 10 minutes
Assessment can be done by…
As a class, show the picture of the dice. Ask students to come up with questions to ask themselves about this image.
Sample questions:
- How many points are there in total?
- How many times do we see the number 6?
- What is the probability of getting a 3?
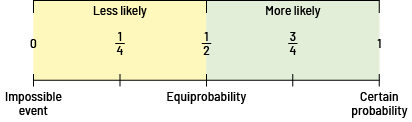
Divide students into small groups and give each group a die numbered 1-6. Ask them to find the theoretical probability of getting an even number. If necessary, review the probability line and associated terminology.
Example of sought-after reflection:
- There are three even numbers, 2, 4 and 6. There are six possible outcomes when we roll a die. The probability of having an even number is therefore \(\frac{3}{6}\).
- The fraction can be simplified to half, which also represents half. On the probability line, this tells us that it is equiprobable whether we get an even or an odd number.
| Possible Observation | Possible Interventions |
| The student does not know where to start. | What should you do first?
What are all the possible outcomes of a roll of the die? What are the even numbers on the die? What is a probability? |
| The student has difficulty expressing probability as a fraction. | What does the numerator represent in probability?
What does the denominator represent in probability? How many sides does the die have in total? Is this total the numerator or the denominator? |
| The student has difficulty expressing the probability of getting an even number as a fraction. | What does the fraction \(\frac{3}{3}\) represent?
(an integer, \(\frac{1}{1}\) or 100%) Is it true that every roll of the die will result in an even number? |
Ask students to find the theoretical probability of getting a multiple of 3 and then the probability of getting the number 4. Students should then place the probabilities on the probability line, as in the first example.
Examples of sought-after thinking:
- There are two multiples of 3 on a six-sided die (3 and 6), and six possible outcomes, so the probability of getting a multiple of 3 is.
- The fraction is equivalent to "1".
Or
- I know that it is between the two.
- There is only one number 4 on a six-sided die, and six possible outcomes, so the probability of getting a 4 is \frac{1}{6}\.
Have students roll the die 20 times and compile the results in a relative frequency table like this one.
| Event | Counting | Frequency | Relative frequency expressed as a fraction |
| I get an even number. | |||
| I get a multiple of 3. | |||
| I get a 4. |
Ask students what they notice about the results.
Do the results represent the theoretical probability? Why? (Write down students' answers to this question for future reference)
Discuss the results and compare them with the probabilities found earlier. Encourage students to question the effect of the number of throws on the outcome.
Course of Action
Approximate duration: 100 minutes
Assessment can be done by…
Ask students to determine the experimental probability of getting an even number by rolling the die 1,000 times.
Example of sought-after reflection:
- 1000 rolls is a lot, and it will take a long time.
- A roll of the dice lasts about 5 seconds, so 1000 rolls is approximately 5000 seconds (5000 seconds is about 83 minutes!).
- With so many throws, one could make more mistakes, for example forgetting to put a result in the frequency table or losing count of the number of throws.
Question students as to whether there is a more efficient way to determine the results of 1000 throws (looking to name the code as a representation tool).
First ask students what the computer should do to count the number of times an even number is rolled after 1,000 rolls of a six-sided die. This will become the pseudocode that will direct the block coding.
Example of pseudocode:
|
Repeat 1,000 times. |
|
Generate a random number from 1 to 6. |
|
Add the number to the list "The list of throws". |
|
If the number = 2 or the number = 4 or the number = 6. |
|
add 1 to the counter "Even numbers". |
The code consists of three parts:
- A code sequence to roll a six-sided die and compile the results.
- A code sequence with a conditional event to determine whether the result of the throw is even or not.
- A sequence of code that will compile the total number of throws resulting in an even number.
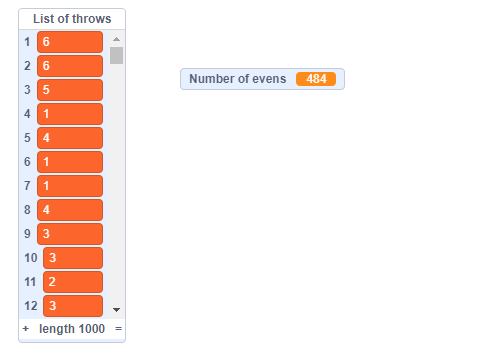
Here is an example of code that determines the number of times an even number is obtained after 1000 throws of the die, based on the above pseudocode.
Events block stating “start one when green flag is clicked.”Variable block stating “set number of evens to ‘0’.”Variable block stating “set throw numbers to ‘1’.”Lists blocks stating “delete all of lift of throws.”Control block stating “repeat ‘1000’.”Inside 2 nested blocks.Variable block stating “set face of die to pick random ‘1’ to ‘6’.”Lists blocks “add Control block “face of die” to list of throws.”Control block stating “repeat” lists block stating “length of list of throws.”Inside one nested shape. Control block stating “if item throw number of list of throws, equals, 2, or item throw number of list of throws, equals, 4.”Inside one nested block.Variable block stating “change numbers of evens by ‘1’.”Variable block stating “change throw number by ‘1’.”
Here is the result generated by this code. The students' code could be different while remaining functional.
| Possible observation | Possible Interventions |
| The student fails to compile the results of the die roll. |
Ask the student to find the number of sides of the die that was given to them.
My blocks stating ”define die throws”.Caption: “A new block called ”die throws is created.
This block includes the code necessary to perform a certain amount, parenthesis, 1000, parenthesis random throws
of a die. -The repeat control block is used with a value of 1000 which execute that many times.-Inside the loop,
we add the set block that assigns a random number between one and 6 that simulates the loss of 6 sides die. -The
results of each toss is then added to a list called “list of throws”. When the loop is completed, there will be
1000 elements, parenthesis, number, parenthesis in the list between one and 6. Controls block stating “repeat
‘1000’”.Inside are 2 nested blocks.Variables block stating “set face of die to pick random ‘1’ to ‘6’”.Lists
block stating “add variables blocks “face of die” to list of throws”.
|
| The student forgets to reset his variables and lists. |
Blocks of code:Events block stating “start on when green flag is clicked.”Caption:These code
block will execute as soon as the green flag is clicked. The die throws will then begin but it's important that
the previous list is deleted (erased). The blocks-set “numbers of events to 0, and-set “throw number” to 1, as
well as-delete all the “list of throws”,-Are necessary so that I can restart the experiment without having the
previous results.Variable blocks stating “set number of evens to ‘0’.”Variable blocks stating “set throws number
‘1’.”Lists blocks stating “deleting all of list of throws.”My blocks stating “die throw number.”My blocks stating
“even numbers.”
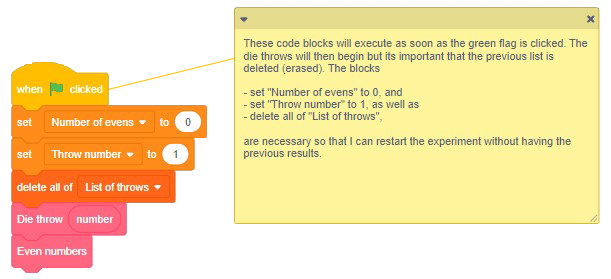
Ask the student to read the code aloud to see if there are any missing instructions. Ask the student to explain the three blocks identified. Ask the student what happens when the variables are not reset. What is the impact on test results?
|
| Student does not use operator blocks correctly. |
 
Ask the student if there is a way to make the computer do more of what is wanted (use the "or" block). Have the student understand that the computer reads one piece of data at a time, so the comma is not useful in programming. The use of the "or" operator block is useful for suggesting several possible answers, such as 2 or 4 or 6 for even numbers.
|
| The student repeats 1,000 times in their even number code rather than repeating the length of the list. | Ask the student where the results of the dice rolls are compiled (the results of the dice rolls should be
compiled in "The Rolling List").
In which list should you find the even numbers? What variable do you need to add to search for even numbers? (I need to add the "length of the roll list", so that the entire roll list will be repeated) Events block ”repeat ’1000’.”2 nested blocks. Control block stating ”if item throw number of list of throw, equals, 2, or, item throw number of list of throws, equals, 4, or item throw number of list of throws, equals, 6, then.”One nested block.Control block stating “change number of events by ‘1’.”Conrol block stating “change throw number by ‘1’.”
Events block ”repeat ’1000’.”2 nested blocks. Control block stating ”if item throw number of
list of throw, equals, 2, or, item throw number of list of throws, equals, 4, or item throw number of list of
throws, equals, 6, then.”One nested block.Control block stating “change number of events by ‘1’.”Conrol block
stating “change throw number by ‘1’.”
|
| Student does not use variables appropriately. | Ask the student what the variables mean. He or she must know the meaning of the variables used in order to
fully understand the code.
Control block stating "face of die”. Caption: “This variable represent the 6 faces of a die.
That is, the number 1, coma, 2, coma, 3, coma, 4, coma, 5, coma, 6 that we find on a die”.Lists block stating
“lift of throws”.Caption: “A list called, quotation, list o f throws, quotation, was created in advance and it
contains all the results of the random die of throws”.Lists block stating “Length of list of throws”. Caption:
“This returns the number of elements in the list, quotation, list of throws, quotation”.Control number stating
“Throw number”. Caption: “The variable, quotation, throw number, quotation, was created to represent each elements
in the, quotaton, list element, quotation, parenthesis, 1000 of them in this case, parenthesis. It iliterates
between 1 and 1000.
|
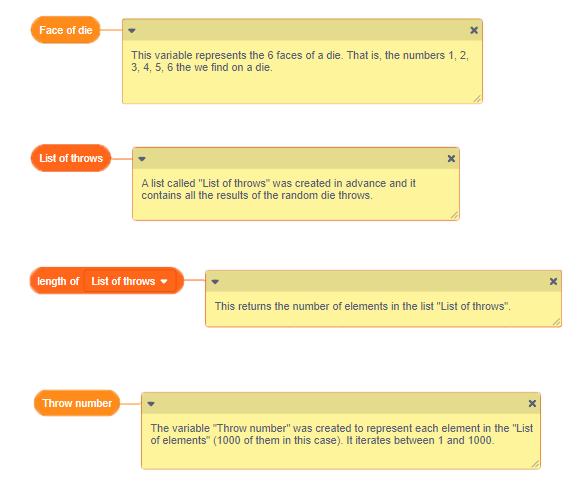
Note: In the examples provided, the notes in yellow are explanations of how the code works and should be omitted when the code is presented to students.
Consolidation
Approximate time: 15 minutes
The evaluation can be done by…
Provide feedback on the activity
- What are the findings?
- Do the results of the experimental probability at 20 throws differ from the results of the experimental probability at 1,000 throws?
- What do you notice between the theoretical and experimental probability?
- In your code, which blocks represent conditional statements?
- Could you use your randomizer or a similar machine in other probability situations? Which ones? Why or why not?
Consolidation
- Suggest that students modify their code to check the experimental probability of obtaining a multiple of 3 or the number 4.
- Suggest that students code to compare the theoretical and experimental probability of drawing a red marble from a bag of 10 marbles knowing that 3 marbles are red (we discuss conditional if/then/otherwise statements in this example).
Links with other mathematical strands
Number
B1.4 Compare and order fractions from halves to twelfths, including improper fractions and fractional numbers, in various contexts.
B1.5 Read, represent, compare, and order decimal numbers to hundredths in a variety of contexts. Conditional statements (if/then/if not) are used to make comparisons between numbers by using them in combination with the "operator" blocks (>, <, =).
Data
D2.1 Use fractions to express the probability of events happening, represent this probability on a probability line, and use it to make predictions and informed decisions.
D2.2 Determine and compare theoretical and experimental probabilities of an event occurring. Conditional statements are used to code in experimental situations with probabilities. The if/then/not terminology is useful in determining certain events in a random experiment.
Financial Literacy
F1.2 Estimate and calculate the cost of transactions involving multiple items priced in dollars and cents, including sales tax, using various strategies.
With the elimination of the 1 cent coin, the total cost is rounded to the nearest 5 cents. By using conditional statements (if/then/if not), it is possible to create rules to follow for rounding (e.g., IF the number in the hundredths position is 1 or 2, THEN change the value to 0. IF the number at the hundredths position is 3 or 4, THEN change the value to 5, etc.).
Differentiated Instruction and Universal Design for Learning
- Give students the disconnected blocks so they can replace them and make a code.
- Give the students the variables before starting the code.
- Suggest a beginning of the code for the student to complete.
- Create some blocks for the student, such as the "multiple of 3" block and the "even number" block.
