C2.3 Solve equations that involve whole numbers up to 100 in various contexts, and verify solutions.
Skill: solving equations
Different types of equations
An equation is a symbolic way of representing a relationship that can be difficult to understand, in part because there are various types of equations that vary in function depending on the situation. In the junior grades, students encounter the following four types of equations:
Equation to solve: An equation such as 2 + n = 14 must be solved. It usually comes from a problem situation and describes an equality relationship. The letter n represents an unknown value that must be determined.
An equation that represents a relationship between two changing quantities: An equation such as c =2n + 3 is used to express a relationship, such as the relationship between the number of a figure(n) in a non-numerical sequence and the number of toothpicks(c) that make up the figure. The letters n and c are variables, since they can take on various values.
Equation that serves as a formula: To calculate the area (A) of a square, we can use the equation A = c × c. Such an equation is called a formula, since it is used to calculate the area of a square with sides of length c. We do not solve such an equation.
Equation that generalizes a situation of equality: We can generalize the relationship of equality between the addition of any two identical numbers and the multiplication of that number by 2 (e.g., \(4 + 4 = 2 \times 4\)) by the equation \(n + n = 2 \times n\). Such an equation is not solved and is not a formula. Moreover, it does not represent a relationship between two changing quantities.
Each of these types of equations is discussed in more detail in the following.
Note: Details of the various types of equations are given to recognize that algebraic concepts are not encountered and treated exclusively in modeling and algebra activities. For example, equations that are used as formulas in measurement are regularly found. However, in the junior grades, students do not necessarily have to distinguish between these types of equations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 89.
Equation to solve
Students learn about these types of equations in the primary grades, usually in the context of modeling and algebra, as well as in the context of numeracy and number sense. They are derived from problem situations and the solution of these equations is often done through concrete representations and illustrations.
In the junior grades, students are exposed to more equations to solve. It is essential that students master the concept of equality as an expression of equilibrium before they begin to solve these equations. In addition, it is important that these equations come from problem situations so that students can make sense of the equations and their solution.
Solving such equations means determining the value of the unknown that maintains the equality. Solving equations must be done in a context of understanding and analyzing the equality. It is therefore important to regularly invite students to explain their approach to solving, to justify their actions and to demonstrate their understanding of the concepts involved in order to prevent solving equations from becoming just a blind application of procedures.
Solving Equations by Systematic Testing
In this elementary strategy, students systematically choose potential values of the variable until one of these values makes the equality true. For example, to solve the equation 2 × p + 6 = 22, students successively choose p = 1, 2, 3… and find that the equality is true when p = 8.
To solve some equations, such as 125 - b = 32, students can use number sense strategies to reduce the number of trials. For example, to solve this equation, it would not be wise to proceed using b = 1, b = 2, b = 3, and so on, as this would take too much time. Students might think as follows: "I know that 125 - 100 = 25, and 25 is close to 32. If I subtract 105, I get 20. I am getting away from the quantity I am looking for. So, I'll subtract a little less than 100. I'll try b = 99, b = 98, and so on."
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 90.
Advantages of solving equations by systematic testing:
- Students highlight what it means to solve an equation, i.e., to determine the value of the variable that maintains equality.
- Students work systematically, not randomly. They can also use their sense of numbers.
Solving Equations by Systematic Testing
- Communication of work done can be disorganized, as it can be difficult to keep track of trials. Students can then be encouraged to keep such records by creating a table of values.
Here is an example of a table of values used to solve the equation 125 - b = 32 :
| b | 100 | 105 | 99 | 98 | 95 | 93 |
|---|---|---|---|---|---|---|
| 125 b | 25 | 20 | 26 | 27 | 30 | 32 |
Note: Some notations should be avoided. For example, to solve the equation 2 × p + 6 = 22, the student who
tries p = 1 should not write "2 × 1 + 6 = 22," since this equality is false. She or he can evaluate
the left-hand side to get 2 × 1 + 6 = 8 or use the equation in interrogative form (e.g., 2 × 1 + 6 
22) or write 2 × 1 +
6 ≠ 22.
Solving Equations by Inspection
In this strategy, students recognize the equality relationship represented by the equation. Students compare the quantities involved and use their number sense to determine the value of the unknown. Here are three examples of solving the equation c + 45 = 98 by inspection.
Example
A student recognizes that he needs to find the number that, when added to 45, adds up to 98. To do this, he uses his number sense. Since he knows that 45 + 45 = 90, he concludes that the number he is looking for is 8 more than 45, or 53.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 91.
Example
A student recognizes that if you take away the same quantity on each side of the equality, the equation is changed, but the equality is maintained.
c + 45 = 98
c + 45 - 45 = 98 - 45
c = 98 - 45
c = 53
Note: It is important that students do this reasoning in steps, otherwise they may simply apply a misunderstood procedure mechanically. In addition, this reasoning can be used to better grasp the concept of inverse operation, i.e., subtraction is the inverse operation of addition.
Example
A student decomposes a number, then compares or cancels the numbers.
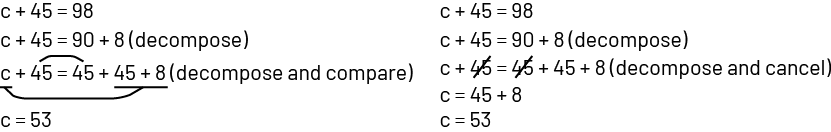
Advantages of solving equations by inspection:
- Students practice decoding the equation, that is, making sense of the symbolism of the equation. Students develop their sense of symbol, equation and equality.
- Students think about operations and numbers instead of trying to use a meaningless procedure.
From the examples above, it is recognized that students can solve the same equation by inspection using a variety of strategies. The strategies "compare terms," "decompose terms," and "modify the equation" that were explored in the analysis of an equality apply very well in equation solving by inspection situations, since the equation represents an equality. Teachers should help students make this connection by pointing out the similarity between an equality and an equation to solve.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 92.
Equation that represents a relationship between two changing quantities
Students learn to represent relationships between two changing quantities using equations. These equations initially express a relationship between two variables, but the opportunity can be taken to convert them into solution equations so that students can substitute values for a variable in an equation and determine the value of the unknown.
We can also reinforce the links between the equation and the table of values.
Example
Here is a sequence of figures. We are interested in the relationship between the rank of the figure and the number of points that compose it.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 93.
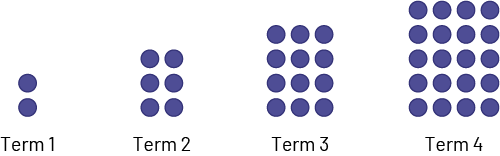
Students might represent the relationship by the equation p = n ×(n + 1), where n is the rank of the figure and pis the number of points in it. The table of values below also represents this relationship.
| Rank of the figure (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of points (p) | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | 90 | 100 |
Source: A Guide to Effective Instruction in Mathematics, Grades 4 to 6, p. 94.
Students can make connections between the equation and the table of values. For example, if n = 1, the equation becomes p = 1 × (1 + 1), hence p = 2, which matches the data in the table. If n = 3, the equation becomes p = 3 × (3 + 1), hence p = 12, which also corresponds to the data in the table. Thus, the question "how many points make up the figure in the 9th row?" can be expressed by the statement "solve the equation p = 9 × (9 + 1)". To solve it, students can use the table of values by looking for the value of p for which n = 9 or perform the calculation and determine that p = 90.
Similarly, a question such as "what is the rank of the figure that has 72 points?" can be expressed as "solve the equation 72 = n ×(n + 1)" because in the equation p = n ×(n + 1), p takes a value of 72. To solve it, students can look in the table of values for the value of n for which p = 72 and conclude that n = 8.
Equation that serves as a formula
In the Sense of Space domain, students learn to express ways of representing area and volume using formulas. For example, in learning to determine the area of rectangles, students discover that the length of the base of the rectangle (e.g., 6 cm) tells them how many square centimetres can be placed in a row. The height of the rectangle (for example, 4 cm) tells them how many rows it can hold. Therefore, the product of these numbers (6 × 4 = 24) indicates the total number of square centimeters the rectangle can hold. Students can generalize this result with a formula, such as A = b × h or A = L × l. In doing so, students can understand the meaning of a formula and the variables that make it up, rather than applying it mechanically.
Source: A Guide to Effective Instruction in Mathematics, Grades 4 to 6, p. 94.
These equations (formulas) formed from variables can also be used to generate equations to solve. For example, the question "What is the height of a rectangle that has a base of 8 cm and an area of 72cm2?" can be translated into algebraic language as "solve the equation 72 = 8 × h ".
Equation that generalizes a situation of equality
Students may encounter these types of equations in particular when exploring the properties of numbers and operations (e.g., m - m = 0). These equations symbolically express the fact that a situation of equality is always true, regardless of the values of the variable(s) that make up the equation(s), and regardless of whether they are natural numbers, fractions, or decimal numbers.
Beginning in the primary grades, students explore certain properties of numbers and operations (e.g., the property of 0 in addition, the commutativity of addition) and make conjectures about these properties using words. In the junior grades, students continue to explore properties and progress to making generalizations using words or an equation. It is important to note, however, that using an equation to generalize a situation of equality requires a good deal of abstraction. Only after developing a good understanding of properties are students able to fully grasp the meaning of such equations.
Source: A Guide to Effective Instruction in Mathematics, Grades 4 to 6, p. 95.
Here are some examples of properties of numbers and operations that are expressed in words and using an equation.
Equality situation
0 + 2230 = 2230
0 + 9,72 = 9,72
Conjecture in words
"When you add any number to 0, you get that number."
Generalization using an equation
0 + m = m
Equality situation
\( 776 - 0 = 776 \)
\(\frac{3}{4} - 0 = \frac{3}{4}\)
Conjecture in words
"When we subtract 0 from any number, we get that number."
Generalization using an equation
m - 0 = m
Equality situation
\(0 \times 15 = 0 \)
\(0 \times \frac{3}{4} = 0 \)
Conjecture in words
"When we multiply 0 by any number, we get 0."
Generalization using an equation
0 × n = 0
Equality situation
1 × 235 = 235
1 × 1,56 = 1,56
Conjecture in words
"When you multiply 1 by any number, you get that number."
Generalization using an equation
1 × n = n
Equality situation
4 + 3 = 3 + 4
Conjecture in words
"When adding two numbers, the order in which they are added is not important."
Note: In the junior
grades, teachers can lead students to recognize that this property also applies to the sum of more than two numbers.
Generalization using an equation
a + b = b + a
Teachers need to support students' journey toward an understanding of equations that generalize an equality situation. The example below describes a step in this direction that leads to the generalization of the distributivity property of multiplication over addition.
Example
Using concrete materials, demonstrate to students that in order to calculate 3 × 24, one can calculate 3 × 20 and 3 × 4 separately, and then sum the products.
Source: A Guide to Effective Instruction in Mathematics, Grades 4 to 6, p. 96.
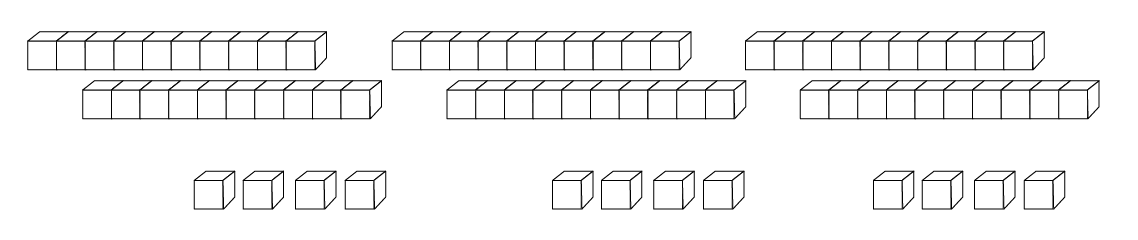
Next, introduce students to various equalities that relate to the distributivity property of multiplication over addition.
Example
4 × 27 = (4 × 20) + (4 × 7)
11 × 34 = (11 × 30) + (11 × 4)
For each, have students explain, represent, and analyze the property by asking thought-provoking questions such as:
- Is equality true? How do you know?
- Can you demonstrate this with concrete materials?
- Can you verify the equality without doing any calculations?
- Would it work with other numbers?
- Can you represent the equality using a rectangular layout?
Throughout the exploration, encourage students to make conjectures related to the equalities presented, such as, "When a number is multiplied by another number, the second number can be decomposed before it is multiplied by the first."
Then introduce students to equations that use distributivity and can be solved easily without performing calculations. For example:
7 × 31 = (7 × 
) +
(7 × 1)
6 × 28 = ( × 20)
+ (6 × 8)
7 × 9 = (3 × 9) +
× 9)
(20 × 8) + ( × 8)
= 23 × 8
Ask questions that lead students to a generalization that the distributivity property of multiplication over addition is true regardless of the numbers used. Ask them to symbolically represent this property with an equation, e.g., a ×(b + c) =(a × b) +(a × c).
Source: A Guide to Effective Instruction in Mathematics, Grades 4 to 6, p. 97.
Knowledge: Equation
Equality relationship that includes one or more variables.
Example
20 + 44 = ____ + 20
a + b = 10
Source : Curriculum de l’Ontario. Programme-cadre de mathématiques de la 1re à la 8e année. 2020. Ministère de l’Éducation de l’Ontario.
Knowledge: variable
Indeterminate term in an equation (symbols or letters) that can be replaced by one or more values.
Example 1
In the equation, 10 = Δ + 9, the triangle is a variable, because the value is unknown. We can replace it with a single value, namely 1, to make the equation true.
Example 2
In the equation 10 = Δ + * or 10 = x + y, the symbols or letters are variables, as they can be replaced with different values.
Source: En avant les maths! grade 3, CM, Algebra, p. 2.