C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in repeating, growing, and shrinking patterns.
Activity 1: The Decreasing Sequence
Here is a table of values that summarizes the number of rectangles and circles in each figure according to their term number.
| Term Number | Number of rectangles | Number of circles |
|---|---|---|
| 1 | 32 | 40 |
| 2 | 29 | |
| 3 | 26 | 32 |
| 4 | 28 | |
| 5 | ||
| 6 | 17 |
Ask students to find the pattern rule and to determine the missing numbers in the table of values.
Ask students questions such as:
- What changes do you see in the figures from one term to the next? Explain your reasoning.
- What are pattern rules for? Justify your answer.
- What does the figure look like in row 0? What does the figure look like in row 5? How do you know?
- What do you think the figure in the 10th row will look like? Check your prediction.
- Do you think it is possible to construct a term in this pattern that has exactly 2 rectangles and no circles? How do you know this?
Activity 2: A Square, Squares
Show students the following pattern and ask them to draw the fourth tessellation.
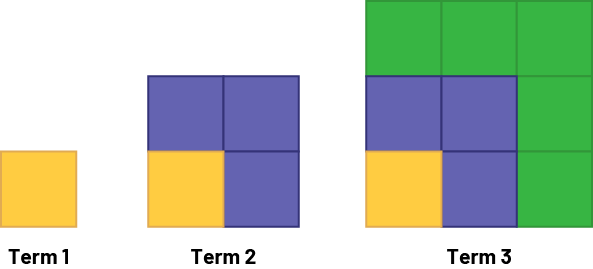
Invite students to identify the pattern rule and use it to draw the fifth tessellation. Then have them create a table of values that represents the relationship between the term number of the tessellation and the number of square tiles that make up the tessellation.
| Term number of the tessellation | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Number of square tiles | 1 | 4 | 9 | 16 | 25 | ? |
To get students to analyze the relationship between the term number of the tessellation and the number of square tiles in it, ask questions such as:
- What is the next number of square tiles to be entered in the table? How did you determine this?
- Will any tessellations following this pattern have 15 square tiles? 49 square tiles? 81 square tiles? 50 square tiles? Explain your answer.
- How can we determine the number of square tiles required to create any tessellation in the pattern?
- How many squares will make up the 10th paving? the 12th paving? the 20th paving?
- What do you notice about each of the numbers of square tiles used?
- What is the relationship between the term number of the tessellation and the number of square tiles it requires?
To help students to recognize that the number of square tiles that make up a tessellation always corresponds to the square of the term number (or the area of the tessellation), read the values from the table aloud (6, 36; 5, 25; 4, 16…).
Encourage students to look at the paving by the number of rows and columns (e.g., the 3rd paving is 3 rows of 3 squares or 3 columns of 3 squares) or to think about multiplication facts.
Extension
Invite students to examine the number of additional square tiles in the pattern of tessellation, from one term to the next. They may recognize that from one tessellation to the next, an odd number of squares is always added.
Create a table similar to the following one.
| Term number of the tessellation | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Number of square tiles of each colour | 1 yellow square | 1 yellow box 3 grey boxes |
1 yellow box 3 grey boxes 3 green boxes |
1 yellow box 3 grey boxes 3 green boxes 7 boxes … |
… |
Using prompts as required, students can formulate the generalization that the sum of the first consecutive odd numbers is always a square number. Then ask them to check whether this generalization also applies to even numbers.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 158-159.
Activity 3: Strategist
Introduce the game Strategist. It is played by two people using a strip like this one:
Here are the rules of the game:
- Starting from "0", the token is moved to the right in turn.
- The token can be moved one or two squares.
- The first person to reach the "8" square loses the game.
Form teams of two students. Provide each team with a copy of Appendix 5.5 (Strategist). Invite students to play the game, noting how the game unfolds on Appendix 5.5 so that they can analyze it and determine patterns in the results.
Example
During the game, ask the question, "Is there a strategy that ensures victory?" A little later, ask the question, "Is there a strategy that allows the person who plays first to secure victory?" Tell students to clearly explain in writing any winning strategy.
Here is an example of a student explanation:
"In order to win, the first player (A) must place the token on square 1. After that, they controls the game. No matter what the other player (B) decides to do, player A must go to square 4 and then to square 7. This way, player B will always have to play a turn from 7 to 8 and… lose. In summary, Player A can always win if they place their token on squares 1, 4 and 7 in succession."
Then invite students to play using a strip containing a different number of squares, and to check whether the winning strategy remains the same or needs to be modified.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 160-161.
Activity 4: One rule, many relationships
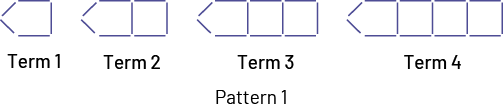
Inform students that they are interested in the relationship between the term number of the figure and the number of toothpicks in it. Invite students to analyze the pattern of figures, extend the pattern, create a table of values that represents the relationship, determine the number of toothpicks in a large term number (e.g., the 10th term), and formulate a pattern rule.
(According to the table of values, the number of toothpicks increases by 3 each time. This can be seen in the
non-numeric pattern because from one term to the next you add 3 toothpicks, i.e 
).
Example of a rule for pattern 1
Each figure is composed of 2 toothpicks and the addition of groups of 3 toothpicks. The number of these groups corresponds to the term number of the figure.
The figure in the 10th row will therefore be composed of 2 toothpicks and 10 times the addition of 3 toothpicks (30), that is 32 toothpicks.
Repeat the same process with the following two pattern:
image Nonnumeric increasing sequence of squares.Rank one, 7 toothpicks.Rank 2, ten toothpicks.Rank 3, 13 toothpicks.Rank 4, 16 toothpicks.Nonnumeric increasing sequence of squares.Rank one, 4 toothpicks.Rank 2, 7 toothpicks.Rank 3, 10 toothpicks.Rank 4, 13 toothpicks.
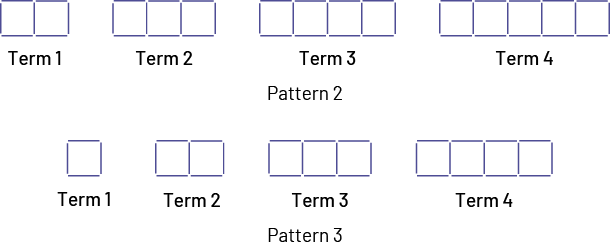
Next, invite students to compare the three situations and the pattern rules that represent the relationship between the term number of the figure and the number of toothpicks in it. Have them recognize that the three situations have the same rule (a new figure is always formed by adding 3 toothpicks to the figure of the previous term in the same way), but that the relationships differ because the base figure (term number 1) is different.
Example of a rule for pattern 2
Each figure is composed of 4 toothpicks and the addition of groups of 3 toothpicks. The number of these groups corresponds to the term number of the figure.
The figure in the 10th row will therefore be composed of 4 toothpicks and 10 times the addition of 3 toothpicks (30), that is 34 toothpicks.
Example of a rule for pattern 3
Each figure is composed of 1 toothpick and the addition of groups of 3 toothpicks. The number of these groups corresponds to the term number of the figure.
The figure in the 10th row will therefore be composed of 1 toothpick and 10 times the addition of 3 toothpicks (30), that is 31 toothpicks.
Next, invite students to describe the numeric patterns that relate to the situations.
Example of answers
Pattern 1: To create the pattern, start with 5, then always add 3 (5, 8, 11, 14, 17…).
Pattern 2: To create the pattern, start with 7, then always add 3 (7, 10, 13, 16, 19…).
Pattern 3: To create the pattern, start with 4, then always add 3 (4, 7, 10, 13, 16…).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 161-163.