C2. Equations and Inequalities
Demonstrate an understanding of variables, expressions, equalities, and inequalities, and apply this understanding in various contexts.
Learning Situation: Number Puzzles
Total Duration: approximately 100 minutes
Summary
In this learning situation, students use algebraic reasoning to create a number puzzle based on a sequence of arithmetic operations.
Learning Goals
The purpose of this learning situation is to have students:- construct a sequence of arithmetic operations;
- concretely and semi-concretely represent a sequence of arithmetic operations with emphasis on a variable;
- use the variable to represent an unknown quantity;
- reason algebraically.
| Learning Context | Prerequisites |
| In earlier grades, students learned to represent situations of equality and simple equations. Using various representations, they also learned to determine the value of the variable in a simple equation. In Grade 6, they are able to represent situations of equality within the framework of more complex contexts by using variables.
They can also determine the value of the variable in an equation by inspection or by systematic trials. |
This learning situation helps students consolidate their understanding of the variable and improve their use of the algebraic concepts under study.
To be able to carry out this learning situation, students must be able to represent simple equations in different ways (concrete, semi-concrete and symbolic). |
Materials
- Appendices 6.1 and 6.2
- Appendix 6.3 (one copy per team)
- large sheet of paper (one per team)
- tokens or cubes
- opaque containers (cups or bags)
Mathematical Vocabulary
variable, representation, equation
Before Learning (Warm-Up)
Duration: approximately 40 minutes
Facilitate a discussion about puzzles so that all students understand their meaning. Follow up by explaining that in this learning situation, students will be asked to understand, explain and create number puzzles.
Note: In the number puzzles below, the starting number is limited to numbers from 1 to 10 in order to restrict the amount of manipulatives and drawings needed for the representations. This restriction also makes it easier to calculate the operations to be performed at each step of the puzzle. However, the puzzle applies to all numbers, large or small.
Ask the students to complete the following puzzle with a piece of paper and a pencil:
- Choose a whole number from 1 to 10.
- Add 6 to this number.
- Subtract 3.
- Add 5.
- Add 2.
- Subtract 10.
Facilitate a discussion to highlight the fact that the result matches the number chosen at the beginning by asking questions such as:
- What do you notice?
- Are there other students who have written this down with other starting numbers?
- How can this be explained?
- Are there any students who did not get their starting number as an outcome?
Note: It is possible that during the discussion some students may bring up the fact that the subtracted quantities cancel out the added quantities; for example, a student might say that throughout the puzzle, 13 was added and 13 was subtracted.
This observation is very interesting, but students should be led to use a generalized representation to show, using a variable, that the puzzle works with all numbers. A model helps to bring out the algebraic reasoning used to solve the puzzle.
Display Appendix 6.1 on the interactive whiteboard or reproduce Appendix 6.1 on a large sheet of paper or erasable board.
Show students an opaque container in which you have placed a certain number of cubes or tokens (for example, 3) without revealing it to the students. Tell them that the container represents the variable, since it contains an unknown quantity of objects. Then represent the operations required at each step using cubes or tokens. Add or subtract from the container. As you proceed, illustrate each step in the Representation Using a Variable column.
Examples of representations of the first number puzzle:
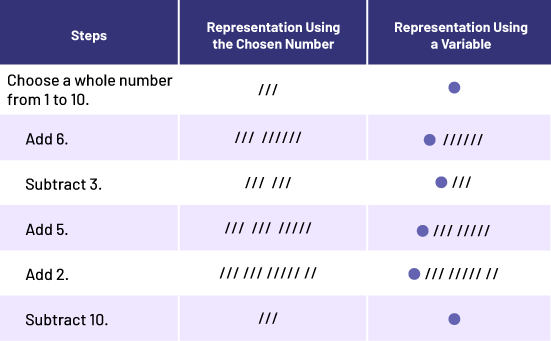
Model the representation of the first number puzzle a second time, but this time showing the number of objects in the container (for example, 3 objects). Represent this number in the first row of the Representation Using the Chosen Number column (see previous example). Add and subtract to eventually show the original number of cubes. As you do so, indicate in the column the operation that was performed. This kind of modelling helps to establish a connection between the two representations.
Next, present the second number puzzle to the students and ask them to perform the operations requested in each step using a piece of paper and a pencil:
- Choose a whole number from 1 to 5.
- Double the number.
- Add 6.
- Double the amount.
- Subtract 4.
- Divide by 4.
- Subtract 2.
Then ask students to compare the number they chose at the beginning with the number they got at the end. Discuss the results.
Group students into teams of two. Provide teams with cubes or tokens. Share Appendix 6.2 with the class. Invite teams to choose a number from 1 to 5 and represent each step of the second number puzzle using the cubes or tokens.
Then invite a team to come and demonstrate the steps of the puzzle. As they do so, reproduce these steps on the board in the Representation Using the Chosen Number column (see example below).
Next, fill in the Representation Using a Variable column with the students (see example below). Discuss the importance of this step in verifying that the puzzle works with any number that is represented by the variable (concretely by the container, symbolically by the square).
Examples of representations of the second number puzzle:

Present the problem in Appendix 6.3 to the class:
It is your turn to create a number puzzle whose result matches the starting number. Your puzzle must include at least six steps, one of which involves multiplication. You will have to show both the Representation Using the Chosen Number and Representation Using the Variable.
Ensure that the task has been understood by asking a few students to explain it in their own words.
Active Learning (Exploration)
Duration: approximately 35 minutes
Group students into pairs and provide them with a copy of Appendix 6.3. Provide them with opaque containers and manipulatives (tokens or cubes) and invite them to complete the task.
Circulate among the teams and support students in their work without telling them how to complete the challenge. Instead, use strategic supports to get them to think about the use of a variable, strategies for creating the puzzle and different forms of representation.
Ask questions such as:
- How can you make sure your number puzzle works?
- Would your puzzle work with any number? How do you know?
Allow sufficient time for students to explore and discuss various strategies for creating the number puzzle.
They can:
- work through trial and error (for example, start with a selected number and formulate a series of operations);
- use manipulatives to represent the puzzle and the variable;
- use manipulatives with a selected number (for example, use interlocking cubes to represent the selected number and perform a series of operations);
- undo operations (multiplying by two and dividing by two, for example).
Example
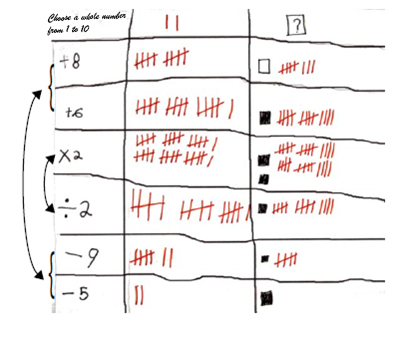
| Possible Observations | Possible Interventions |
|---|---|
| Some teams struggle to create a number puzzle that works with any number. | Encourage students to use the manipulatives to create the number puzzle. |
| One team begins with subtraction and has difficulty representing this step with concrete materials when the starting number is unknown. |
Ask questions such as:
|
| A team begins with a division and represents this step by separating the variable into parts. However, at the end of the puzzle, the team is left with only part of the variable. | Remind the students that they must arrive at the end of the puzzle with the same symbol as at the beginning. |
Have students record their puzzles and representations on a large sheet of paper.

Select teams to present the various strategies used to create a puzzle. Sometimes it is helpful to discuss a strategy that did not work as expected, as when the number puzzle does not work. This gives students the opportunity to co-develop alternatives.
Consolidation
Duration: approximately 25 minutes
Ask the selected teams to come up, one at a time, to explain their number puzzle and its representations.
After each presentation, other students enrich the mathematical conversation by asking questions and making relevant observations in a respectful learning community.
Intervene, as needed, by asking students questions such as:
- How can you make sure your number puzzle works?
- Can we try the puzzle with other numbers? Pick some numbers.
- Does this sequence of operations work with all numbers? How do you know?
- If you were to create another puzzle, what would you do differently? What would you do the same way?
Note: The purpose of this last question is to point out that using the variable, represented by a square, cup, bag, etc., makes it easier to create the puzzle. Emphasize that using a variable ensures that the puzzle works with all numbers. Remind students that a symbol has the same meaning throughout the same situation, in this case, throughout the sequence of operations.
As the Consolidation of Learning progresses, point out the similarities and differences between some of the number puzzles. Some possible findings include:
- Many puzzles begin with an addition.
- Some teams performed a division to cancel a previous multiplication.
- In some puzzles, a step cancels a previous step; for example, + 3, and later, - 3.
- Addition increases quantities, while subtraction decreases them.
- In this puzzle, 6 is added in one step (for example, +6), while in the other, it is added in two steps (for example, +2, followed by +4).
- When multiplying, it must be applied to the entire previous quantity.
Differentiated Instruction
The activity can be modified to meet the different needs of the students.
| To Facilitate the Task | To Enrich the Task |
Example 
|
|
Follow-Up at Home
At home, students can create a number puzzle, test it with a few family members to see if it works, and then explain why it works for all numbers. The next day, teachers can invite a few students to present their puzzle to the class and to explain the strategy used to create it.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 173-183.
