C3.2 Read and alter existing code, including code that involves conditional statements and other control structures, and describe how changes to the code affect the outcomes and the efficiency of the code.
Activity 1: Coordinates
Present students with the following code:
Cartesian plane in scratch, with a cat Sprite in the middle. The coordinates of the extreme left of the abscissa (opening parenthesis) "x" 240 : "y" zero (closing parenthesis). The coordinates of the far left of the abscissa are: (opening parenthesis) "x" minus 240: "y" zero (closing parenthesis). The coordinates at the top of the ordinate are: (opening parenthesis) "x" zero, "y" 180 (closing parenthesis). And the coordinates at the bottom of the ordinate are: (opening parenthesis) "x" zero, "y" minus 180 (closing parenthesis).
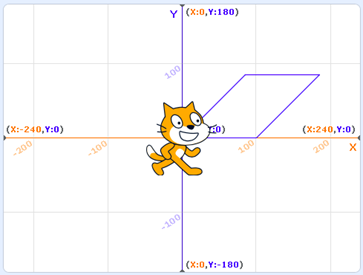
Ask students to explain what is happening.
- Using pseudocode, explain what is happening.
- What are the coordinates of the shape above?
Possible pseudocode to explain the visual:
Start at coordinate (0, 0)
Activate the "pen".
Advance 100 steps, rotate 45 degrees.
Advance 120 steps, rotate 135 degrees.
Advance 100 steps, rotate 45 degrees.
Advance 120 steps, rotate 135 degrees.
It is also possible to use the approximate coordinates in the pseudocode instead of the angles.
Start at coordinate (0, 0)
Activate the "pen".
Go to (100,0).
Go to (180, 80).
Go to (80, 80).
Go to (0, 0).
Code leading to visual to show students:
Blocks of code:Events block stating, “start on when green flag clicked.”Pen extension stating, “erase all”.Motions blocks stating, “go to x: 0 y: 0”.Motions block stating, “pointing in direction 90”.Pen extension stating, “pen down”.Control blocks stating, “repeat 2”Inside 4 nested blocks. Motions block stating, “move 100 steps”.Motions block stating, “turn left 45 degrees”.Motions block stating, “move 120 steps”.Motions block stating, “turn left 135 degrees”.
Present students with the following code:
Cartesian plane in scratch, with a cat Sprite in the middle. The coordinates of the extreme left of the abscissa (opening parenthesis) "x" 240 : "y" zero (closing parenthesis). The coordinates of the far left of the abscissa are: (opening parenthesis) "x" minus 240: "y" zero (closing parenthesis). The coordinates at the top of the ordinate are: (opening parenthesis) "x" zero, "y" 180 (closing parenthesis). And the coordinates at the bottom of the ordinate are: (opening parenthesis) "x" zero, "y" minus 180 (closing parenthesis).The sprite has traced a path on the Cartesian plane.
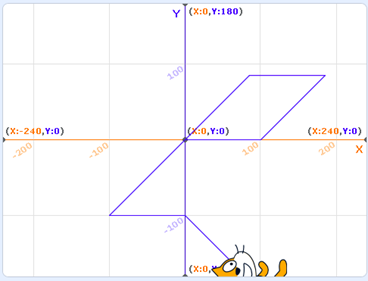
If we want to translate 100 units to the left and 100 units down, what change should we make to the code?
Possible student responses:
- We need to go from the point (0, -100) to the point (100, 0)
- We need to change the angle at which the sprite will turn to the point (0, -100)
- We must use the additional angle to the one used to make the code (instead of turning 135 degrees, we must turn 45 degrees)
Code leading to visual to show students:
Blocks of code:Events block stating, “start on when green flag clicked.”Motions blocks stating, “go to x: -100 y: -100”.Pen extension stating, “pen down”.Motions block stating, “move 100 steps”.Motions block stating, “turn right 45 degrees”.Motions block stating, “move 120 steps”.Motions block stating, “turn right 135 degrees”.
Activity 2: Geometric Shapes
Introduce students to the code below and ask them to explain what is happening using pseudocode.
Blocks of code:Events block stating, “start on when green flag clicked.”Motions blocks stating, “go to x: 0 y: 0”.Motions block stating, “pointing in direction 90”.Looks block stating, “hide”.Pen extension stating, “erase all”.Pen extension stating, “erase all”.Control blocks stating, “repeat 4”Inside 2 nested blocks. Motions block stating, “move 30 steps”.Motions block stating, “turn right 90 degrees”.
Possible pseudocode:
At the start, the sprite goes to (0, 0) and moves to the right.
All pen marks are erased and the pen is in writing position.
Repeat 4 times
Advance (30 steps)
Turn (90 degrees)
The result will be a square: 4 congruent sides, 4 angles of 90 degrees.
Ask students to alter the code so that it draws an equilateral triangle.
Possible questions
- How many sides will a triangle have? (3, so you will have to change the number of repetitions in the loop)
- What are the interior angles' measurement of an equilateral triangle? (60 degrees, so you will have to change the value of the "turn" block).
Please note! The interior angles are 60 degrees, but it is possible that the chosen software interprets the angle as an exterior angle. If this is the case, the program will have to use 120 degrees and not 60 degrees to make the equilateral triangle. This can become a rich mathematical conversation.
Use the same questioning to get students to alter the code to create a hexagon.