C2.4 Solve inequalities that involve multiple terms and whole numbers, and verify and graph the solutions.
Skill: Solving Inequalities and Verifying and Graphing Solutions
To facilitate the learning of the concept of inequality, it is important to provide students with activities that encourage them to analyze situations of inequality and to treat them algebraically. It is then essential to discuss with them the strategies used to analyze inequalities, emphasizing those that call on concrete and semi-concrete representations, and that focus on the meaning of the inequality rather than on the mechanical application of a procedure or tedious calculations.
Graphing solutions on a number line allows students to analyze an inequality using their number, operations and symbol sense, and to find the range of valid values in an inequality situation.
Students need to consolidate this strategy, as it is the basis for a good understanding of the algebraic manipulations they will be exposed to in later grades. Students can also use these strategies to solve simple equations.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, p. 200.
Graphing Solutions on a Number Line
This strategy involves carefully reading the given number sentence and replacing the variable to find the range of valid values in the inequality situation. A table of values is used to find several values for the variable. Then, the solution can be graphed on a number line.
Example
7y + 31 ≥ 78
The first column in the table of values represents the number by which the variable y will be replaced in the algebraic expression 7y + 31.
The second column in the table of values represents the solution of the algebraic expression when the variable y is replaced by the number in the first column.
\(7 (0) + 31\)
\(0 + 31\)
\(0 + 31 = 31\)
The third column in the table of values confirms or refutes the validity of the value of the variable y.
Is \(31 ≥ 78\)? The answer is no.
| y | 7y+31 | ≥78 |
|---|---|---|
| 0 | 31 | no |
| 1 | 38 | no |
| 2 | 45 | no |
| 3 | 52 | no |
| 4 | 59 | no |
| 5 | 66 | no |
| 6 | 73 | no |
| 7 | 80 | yes |
| 8 | 87 | yes |
| 9 | 94 | yes |
| 10 | 101 | yes |
The range of valid values can be graphed using a number line:
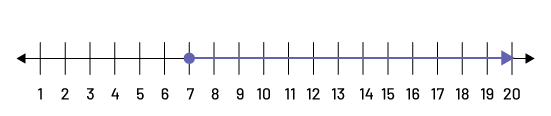
The solution is therefore y ≥ 7.
Note: A number line shows the range of values that hold true for an inequality by placing a dot at the greatest or least possible value. An open dot is used when an inequality involves “less than” or “greater than”; if the inequality includes the equal sign (=), then a closed dot is used.
Once the student has solved an inequality, checking its solution by inserting that value into the original inequality is a great habit to get into.
Example
When solving the inequality 5m - 4 < 2m + 8, it is best to group like terms with a variable on the side where the coefficient is highest (most positive), in this case on the left.
We obtain m < 4.
To check if the solution is true, we can replace the value of m by values around 4, for example 3, 4 and 5.
\(\displaylines{\begin{align} 5(3) - 4 &< 2 (3) + 8 \\ 15 - 4 &< 6 + 8 \\ 11 &< 14 \end{align}}\)
This is true.
\(\displaylines{\begin{align} 5(4) - 4 &< 2(4) + 8 \\ 20 - 4 &< 8 + 8 \\ 16 &< 16 \end{align}}\)
This inequality is false.
\(\displaylines{\begin{align} 5(5) - 4 &< 2(5) + 8 \\ 25 - 4 &< 10 + 8 \\ 21 &< 18 \end{align}}\)
This inequality is false.
Knowledge: Inequality
Relationship of order between two expressions or two quantities. There are four inequality symbols:
<, which means "less than";
>, which means "greater than";
≤, which means "less than or equal to";
≥, which means "greater than or equal to".
Non-Equality
Relationship between two expressions or two quantities that do not have the same value.
Non-equality is represented by the sign "≠" (does not equal, does not equal).
Example
\(\displaylines{\begin{align} 5 &≠ 5 +1 \\ (3 \times 5) + 4 &≠ 3 \times (5 + 4) \\ 8a &≠ 25 \end{align}}\)
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, p. 70.