C1.4 Create and describe patterns to illustrate relationships among integers.
Activity 1: Accurate Predictions Using Number Patterns
Divide the class into teams and give them a situation. From this, students individually create a number pattern representing the situation (encourage students to use a table of values to organize their data). Between them, students then describe their pattern rule. Each situation should lead the student to predict an outcome.
A) Marius plays with his calculator to find the answer to some expressions.

- Can you deduce the result of the next expressions?
- What would be the result of (500) + (-500)? What do we call two numbers that add up to 0?
- What happens if I reverse all the signs, for example (-1) - (+ 1)?
- Make a table of values to explain the result. Can you predict the result of (-100) - (+100)?
B) Leslie plays with tokens and arranges them in the shape of a pyramid, as in the following figure.
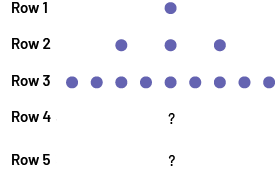
She loves to find recursive relationships in her creations. She also likes to analyze them to describe functional relationships and to help her, she creates a table of values.
| Term Number | Number of Tokens |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 9 |
| 4 | ? |
| 5 | ? |
- She would like to continue her creation, but she does not have enough tokens. However, she notices that there is a pattern rule in her table of values. Do you notice it too? Explain your answer.
- Leslie wants to continue building her pyramid. How many tokens does she need to create the first 10 rows? Is this realistic?
- How many tokens would the 20th row have? Can you explain your answer using a functional relationship?
Activity 2: Grains of Rice (Number Pattern and Relationship Between Numbers)
Materials
- chessboard;
- rice grains;
- calculator.
Divide students into teams. Present them with the scenario below. Each team must answer the questions. Discuss the proposed strategies as a class.
Situation
Antonio likes to play with numbers and create patterns. In his room, he has a chessboard like the one below. He uses it to create a new number pattern.

He places grains of rice on the squares. On square A1, he places 1 grain of rice, on square B1, 2 grains of rice, on square C1, 4 grains of rice, on square D1, 8 grains of rice and so on.
He would like to cover all 64 squares of the chessboard.
- How many grains of rice will be in square H1 (last square in the first row)? How do you know?
- Do you think he will be able to put rice on all the boxes? Justify your answer.
- How many grains of rice should he place on the 64th square of the board? Describe the number pattern you would use to find this answer.
Activity 3: The Multiplication Table
In a multiplication table, there are several number patterns. Using the table below, invite the students to create number patterns. The students should be able to find relationships between the numbers in the pattern and describe them to their peers.
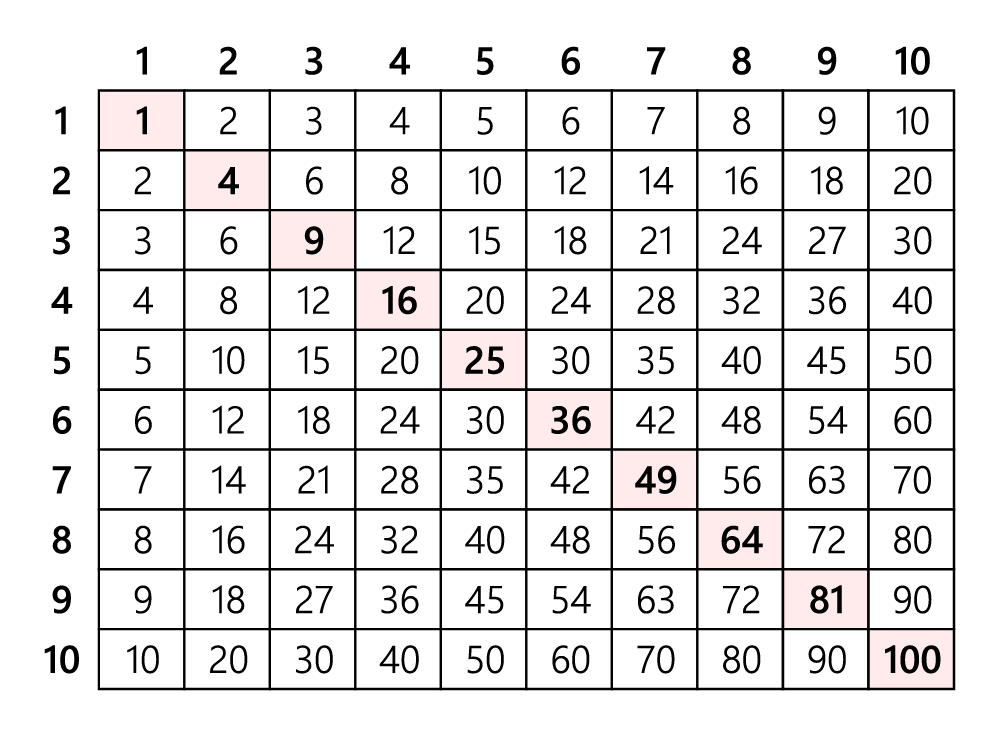
Examples of Possible Patterns
Even numbers, square numbers, the sequence of factors of 10. Lead the student to create and find relationships with shrinking patterns.
Sample Questions
- What type of numbers does the main diagonal represent? What do you notice about the column and row where the square number is located about its value? (For example, column 3 and row 3, the value of the square number is 9.)
- What do you notice about the numbers in row 2 and row 4? Explain your answer.
- What are the numbers in row 2 called?
- Do the numbers in row 4 have the same properties as those in row 2? Explain your answer.
- What do you notice about the numbers in row 10?
To take this further, invite the students to make generalizations and predictions for the 20 × 20 multiplication table.
