C2.3 Solve equations that involve multiple terms, whole numbers, and decimal numbers in various contexts, and verify solutions.
Activity 1: Strategies for Solving Equations
What strategies can be used to solve the equation below and find the value of m?
2m + 3 = 12
Strategy 1
Reverse Logigram
I use the reverse flow chart. The first flow chart shows the sequence of operations applied to the variable to obtain the result. The second flow chart shows the sequence of the reverse operations to find the value of the variable.
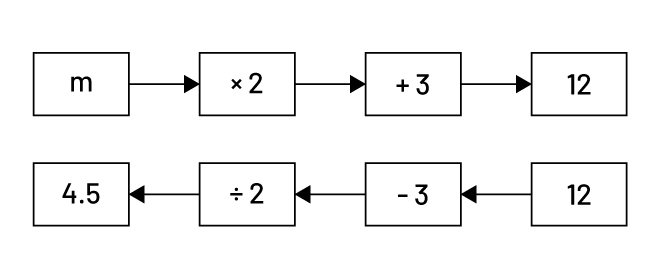
The value of m is 4.5.
Strategy 2
Balance Model
When I use the balance model, I represent the expressions visually and manipulate them until they are equivalent.
I try to collect the unknown values and isolate them from the known values. To isolate 2m, I have to neutralize 3. What I do on one side of the expression, I also do on the other. So I remove 3 from each side of the expression.
\(\ 2m \ + \ 3 \ - \ 3 = 12 \ -\ 3\) \(\ 2m = 9\)I then divide each side by 2 to get the value of m.
\(\frac{2}{2}m \ = \frac{9}{2}\) \(m = 4,5 \)The value of m is 4.5.
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 3.
Activity 2: Solving Equations
Solve the problems below and then check your solutions.
- \(3x + 5 = 7x - 3\)
- \(3.5k - 12 = 0.4k + 5\)
- \(-3.1f + 6.2 = 5.5f+ 1.8\)