C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in growing and shrinking patterns involving rational numbers, and use algebraic representations of the pattern rules to solve for unknown values in linear growing and shrinking patterns.
Activity 1: Pattern Rules for Growing and Shrinking Patterns
Divide the class into teams. Give them a situation that involves that involves a growing pattern and a situation that involves a shrinking pattern. Have them represent their situations, identify their pattern rule, and solve related problems.
Examples of situations
1. Sophia buys a membership at a gym. She has to pay a $35 registration fee. In addition, there is monthly fee of $45.50.
- Create a table of values that represents the relationship between the fees and the number of months in a year.
- What type of pattern is this? Justify your answer.
- What is the initial value and what is the constant rate in this pattern?
- Use an algebraic equation to answer the following question: With $490, how many months of membership can she afford?
Source: translated from En avant, les maths!, 8e année, CM, Algèbre, p. 4.
2. For the following repeating pattern, create a table of values to represent the relationship between the term number and the term value (number of squares).
- Use an algebraic equation to determine the term number that will have 99 squares.
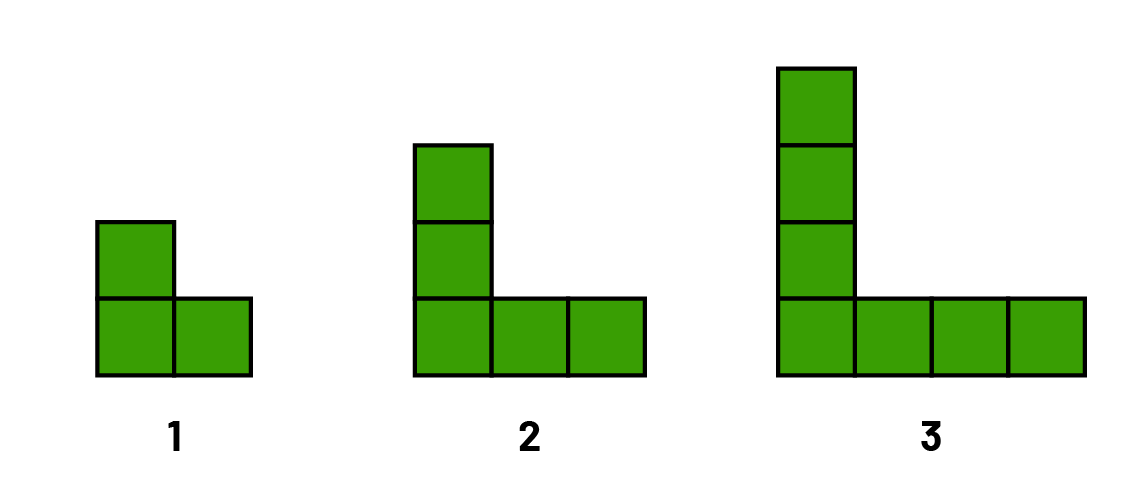
Source: translated from En avant, les maths!, 8e année, CM, Algèbre, p. 6.
3. A plumbing company offers its services to do work in the home at a cost of $80 per hour, plus a $100 service call fee.
- Create a table of values that represents the relationship between the total invoice amount and the number of hours required to complete the work.
- What type of pattern is this? Justify your answer.
- What is the initial value and what is the constant rate in this pattern?
- What will the bill be if it takes five hours to complete the work?
- Use an equation to determine the number of hours needed to complete the work if the cost of the invoice is $380.
Activity 2: Carousel of Patterns
Divide the class into teams. Have teams circulate to the different stations (about 10 minutes per station; and then rotate). Provide different cards at each station which contains a situation and have students answer a series of questions. Circulate and record students' different strategies. Involve the teams in the feedback.
Examples of Stations in the Carousel
Station 1
The following table of values represents the number of necklaces made by Jalal during his shift:
| Number of Hours (h) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Number of Necklaces (n) | 1.5 | 3 | 4.5 |
- How many necklaces does Jalal make in 3 hours? 8 hours? 12 hours?
- Write an equation representing the relationship between the number of necklaces Jalal makes to the amount of time working.
Station 2
The temperature a week ago was 23 degrees and it has been decreasing by 0.75 degrees every day for the past week.
- Represent the situation using a table of values, showing the temperature for each day of the past week.
- Write an equation representing the change in temperature in the past week. Explain what the constant rate means in this situation.
- If this steady decrease continues, what will the temperature be after five days?
Station 3
The following table of values represents the relationship between total cell phone costs and the number of months it is used.
| Number of Months of Use (n) | 0 | 2 | 5 | 10 |
|---|---|---|---|---|
| Total Cost (c) | 500 | 575.40 | 688.50 | 877 |
- Why is the total cost $500 at zero months?
- What is the total cost after 1 month of use?
- Determine a pattern rule that represents this situation and write it as an equation.
- What will be the total cost of the cell phone after using it for 1 year?
