D2.1 Use mathematical language, including the terms “impossible”, “possible”, and “certain”, to describe the likelihood of events happening, and use that likelihood to make predictions and informed decisions.
Skill: Using Mathematical Vocabulary to Express the Probability of an Event Happening
In the primary grades, students develop probabilistic thinking on a daily basis through the learning of certain words or phrases that describe the frequency or likelihood of various events (for example, "We always have Saturday and Sunday off," "It's possible that I'll play ball at recess," and "It's unlikely to rain today."). Students also develop an understanding of the concepts of variability and chance by conducting simple probability experiments. Although their understanding of theoretical probability is still in its beginning stages, they can recognize, for example, that by spinning a spinner that has been separated into thirds, there is a one-in-three chance that the arrow will come to a stop on the third that is coloured red.
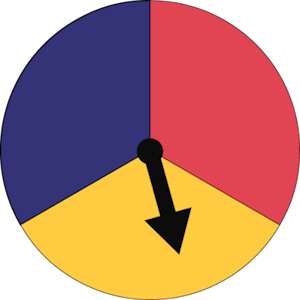
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 128.
In the primary grades, one of the first indications of the meaning of variability occurs when pupils are able to state whether it is certain, possible or impossible that a given event will occur (for example, " It is impossible that cows start to fly.”). Some students have great difficulty doing this. For many, what is possible becomes certain. For example, if the teacher tells them that it is possible that they will bring their dog to class the next day, the students will be very disappointed if this does not happen, since in their minds, it is certain that the teacher will bring it. They must understand that if an event is possible, it is as likely to happen as not happen. Other students have difficulty distinguishing between what has never happened and what may never happen. For these students if an event never happened, it is impossible. For example, they may think it's impossible for them to go a whole night without sleep because they've never done it. However, such an event is not impossible.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 132-133.
Skill: Making Predictions and Informed Decisions
According to the big ideas Collection and Organization of Data and Data Relationships, the recommended problem-solving approach uses the process of inquiry. This approach fosters critical probabilistic thinking by encouraging students to formulate conclusions from data collected in probability experiments and to question their intuition about the probability of one of the outcomes. Such an approach helps to avoid the development of some of the misconceptions about probability that are too often found in both students and adults.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 128.
Knowledge of concepts related to probability helps students better understand all kinds of everyday situations (for example, understanding weather forecasts, possible outcomes of an experiment, the probability of winning in a drawing or game). The Probability big idea emphasizes the importance of probabilistic thinking to inform decision making in situations where the outcome is uncertain due to chance.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 127.
Concept of Probability
Probability describes the degree of certainty with which a particular outcome or event can be predicted to occur in a situation of variability. Developing an understanding of the concept of probability is a long process that begins in the early grades. However, it is very important to build on an intuitive understanding of the concept first. In the primary grades, students are able to intuitively recognize that in a given situation, certain events are possible and that the degree of certainty that they will occur is on a continuum from impossible to certain. The probability line model is an effective visual means of describing this continuum.
Image Under the title "Probability Line", the word "possible" appears between two arrows pointing to the extremes of the progressive bar below. The bar starts with white and gradually turns dark blue. On the far left is the word "impossible", and on the far right is the word "certain".
Students approximate a point on this continuum to describe how certain they are that a particular event will occur. The further to the right of the line, the more certain they are. If they place it in the middle, it means that they believe that the event has as much chance of occurring as not.
As students gain experience in solving situations of variability, some tend to develop misconceptions. One of the most common misconceptions relates to the imposition of implicit limits on variability. For example, in a game of heads or tails, students get tails five times in a row. If they are then asked to predict the result of the next toss, many will tend to indicate that it will certainly correspond to the heads side because their intuition leads them to believe that there is a limit to chance favouring the tails side. Teachers should help them understand that chance has no memory, that is, each result is independent of previous results and cannot be predicted with certainty. It is therefore just as likely to get tails as to get heads on the next flip. This kind of misunderstanding persists among adults who believe, for example, that certain numbers have a better chance of being part of the winning numbers in the lottery simply because they have come up more often in the past. A good understanding of the concept of variability makes it possible to recognize that this is not the case. To help students grasp this concept, teachers should introduce them to many simple probability experiments and encourage them to question themselves and be objective about their intuition.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 133-134.
Knowledge: Impossible, Possible and Certain
ImageUnder the title "Probability Line", the word "possible" appears between two arrows pointing to the extremes of the progressive bar below. The bar starts with white and gradually turns dark blue. On the far left is the word "impossible", and on the far right is the word "certain".
- The words impossible and certain describe the two ends of the continuum representing the likelihood of an event or outcome occurring. They are fixed points that serve as anchors.
- An impossible event is an event that can never happen. A certain event is an event that will always happen.
Note: The inverse of these two propositions are not necessarily true. Thus, in the context of an experiment, even if a result never occurred, it does not mean that it is impossible for it to occur. Similarly, the fact that one always obtains some result after a certain number of trials does not necessarily imply that one is certain to obtain it after all trials.
- The word possible describes all events or outcomes that are neither certain nor impossible.
- The location of an event or outcome on the line of certainty reflects the assessment of the likelihood that the event or outcome could occur.
- An event or outcome that is located in the center of the line of probability is as likely to occur as not.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Traitement des données et probabilité, p. 25.