D1.5 Determine the mean and the median and identify the mode(s), if any, for various data sets involving whole numbers, and explain what each of these measures indicates about the data.
Skill: Explaining what Measures of Central Tendency Indicate About the Data
Statistical measures are numbers used to describe a set of data. For example, the mean is a statistical measure. Statistical measures are presented as part of the fourth step in the inquiry process, interpreting results, because they are another way of assigning meaning to data and can provide information on which to base a decision.
Various statistical measures are commonly used in data processing. Those studied in the junior division are range, mode, median and mean. Students need to understand what each represents in order to select, determine and use them appropriately.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 107.
Knowledge: Mode
The mode of a set of data represents the data with the highest frequency, in other words, the data that appears most often. The mode is particularly meaningful in inquiry contexts where we are trying to determine what is most popular, most sold, most frequent, etc. As the following examples illustrate, it is possible to determine the mode of a quantitative or qualitative set of data.
Example 1
The table below presents the data corresponding to the number of children in the families of the students in the class. It can be seen that the most frequent data is two, indicating that there are more families with two children. The mode for this set of quantitative data is therefore two children per family.
Number of Children in the Families of the Students in the Class
| Number of Children in the Family | Number of Students |
|---|---|
| 1 | 3 |
| 2 | 12 |
| 3 | 6 |
| 4 | 3 |
| more than 4 | 2 |
Example 2
The graph below looks at the preferred colours of the students in the class. To determine the mode of this qualitative data, we need only investigate the length of the bars. We see that the red and blue bars are equal in length and are longer than all the others. In this case, there are two modes, red and blue.
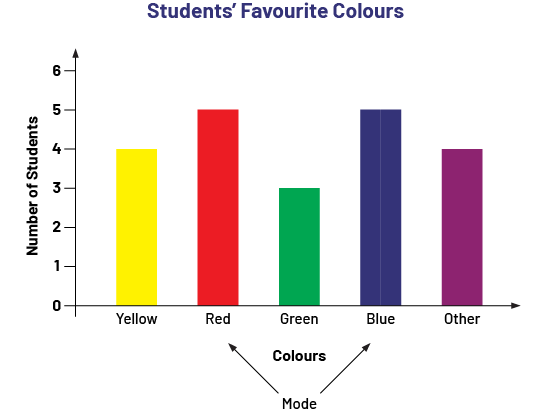image The coloured 5-bar graph is titled: "Students’ Favorite Colours". The horizontal axis is named "Colours", while the vertical axis is named "Number of Students". The yellow bar goes up to the number 4. The red bar goes up to number 5. The green bar goes up to the number 3. The blue bar rises to the number 5, and the purple bar meaning "Other" rises to the number 4. With arrows, the word "mode" points to the red bar and the blue bar.
When using the mode to answer a question of interest or to make a decision, it is important to consider the entire data set. This is because in some situations, the most frequent data is not necessarily the one that makes the most sense of the data. It is important to encourage students to investigate every situation closely before making conclusions based on the mode.
Examples of situations in which the mode is an appropriate measure of central tendency to use as a representative of the data include :
- In example 1 above, the mode of two children per family seems fairly representative of the situation, since there is a large gap between this characteristic and the others.
- In example 2, not only are there two modes (red and blue), but the difference between their numbers and the other frequencies is not very large. It is therefore difficult to conclude that these two modes represent a strong colour preference. In this case, it would be better to mention that red and blue are slightly more popular, but that yellow follows closely behind.
- From the stem-and-leaf plot below, the mode corresponds to 72 heartbeats per minute. It can be seen that this number is also in the range (70 to 79) with the most data. Therefore, it can be concluded that it represents this set of data well.
Number of Heartbeats Per Minute of Students in the Class
| 6 | 3 5 5 8 9 |
| 7 | 1 1 2 2 2 2 2 4 5 7 7 |
| 8 | 2 3 6 |
| 9 | 1 2 |
| 10 | 8 |
- From the line plot below, the mode corresponds to 60 heartbeats per minute. We can see that this number is far from the interval that counts most of the data (69 to 77). Furthermore, we see that the range of the data (29) is large and that the data appear only once, twice or three times each. Therefore, it would be best not to use the mode to make a conclusion about this set of data.
image The number line is titled "Students’ Number of Heartbeats Per Minute". It is graduated from 60 to 90. With an arrow, the word "mode" points to the number 60. The numbers that have no X's are: 61, 63, 64, 65, 66, 68, 78, 79, 80, 82, 83, 84, 86, 87, 88, and 90. The numbers 62, 67, 69, 70, 71, 74, 76, 77, 81, 85 and 89 have an X. The numbers 72, 73 and 64 have two X's. The number 60 has three X's.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 108-111.
Knowledge: Mean
In mathematics, mean has a more precise meaning: it corresponds to the value resulting from an equitable division (equal sharing). For example, if five friends have raised $5, $7, $7, $8, and $8, respectively, and they pool those amounts to share equally, each will receive $7. The mean of the amounts collected is therefore equal to $7. In more advanced mathematics, this mean is called the arithmetic mean. Other means exist (for example, geometric mean, harmonic mean), but they are not under study in the junior division. Teachers should emphasize the understanding of the concept of mean rather than the memorization of the algorithm to compute it (sum of data divided by number of data). To do this, they should provide students with activities that use the equal share model or the balance model between the sum of the shortages (differences between the average and the data that are below the average) and the sum of the surpluses (differences between the mean and data that are greater than the mean). Otherwise, students gain only a limited understanding of the concept of mean.
Equal Share
The examples below demonstrate different situations that use the equal share model and help develop a good understanding of the concept of a mean. The equal share model can be used to determine a mean without having to use the standard computational algorithm.
Example 1
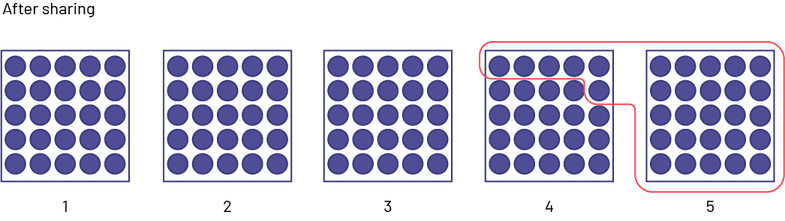
Amir, Bruno, Carla, Denis and Elmira went fishing and caught 2, 2, 3, 3 and 10 fish respectively. Determine the average number of fish caught.
To determine the average number of fish caught, students can determine how many fish every person would have if the fish were equally distributed. Students can first illustrate the initial situation as follows.
Then the students proceed to the sharing: Elmira gives two fish to Amir, two fish to Bruno, one fish to Carla and one fish to Denis.
After sharing, each person has four fish, so we can conclude that on average each person caught four fish.
In order to deepen the concept of mean, it is important to give students the opportunity to reverse the process by asking them to create a set of data with a given mean. This reinforces the concept of mean as the result of equal sharing.
Example 2
Six students in a class determined that they had, on average, five pens each. What might be a possible distribution of pens among these six students?
Since the six students average five pens each, each student would have five pens after the equal share.
This gives a total of 30 pens (6 × 5).The six students can then divide the 30 pens among themselves as they see fit. Regardless of the division chosen, the average of five pens per student will be maintained. Here is an example of a possible division:
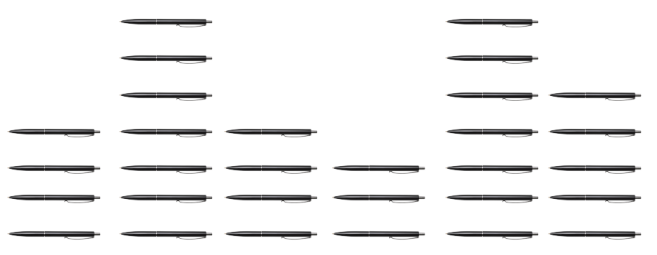
We can verify that there are still a total of 30 pens.
One can use the sharing model to develop an understanding of the usual algorithm as illustrated in the example above. The model does, in fact, make sense of the usual algorithm, since it demonstrates the idea of grouping pens and then sharing them among friends (quotient of the sum of the data by the number of data).
Example 3
Annie, Bahéya, Carl, Daniel and Eva have $5, $6, $6, $8 and $10 respectively. How much money does each person have on average?
First, the money is pooled to find that there is a total of $35. This is equal to $5 + $6 + $6 + $8 + $10 = $35. The money is then divided equally and each person receives $7, which is equal to $35 ÷ 5 = $7.
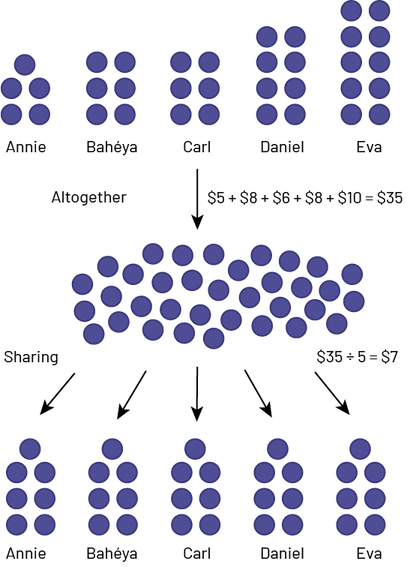image At the top of Example 3, five student names each have a few red chips. Annie has 5 chips, Bahéya has 6 chips, Carl has 6 chips, Daniel has 8 chips and Eva has 10 chips. Under the names it says: Altogether, 5 dollars plus 6 dollars plus 6 dollars plus 8 dollars plus 10 dollars equals 35 dollars. An arrow points to the middle of Example 3 where all the chips are pooled for a total of 35. Below the pile of 35 chips, it says: Sharing, 35 divided by 5 equals 7 dollars. Under the cluster of 35 chips, 5 arrows point down to each of the names that are repeated and where the chips are redistributed equally. Annie, Bahéya, Carl, Daniel and Eva each have 7 chips.
Teachers can use this example to emphasize to students that the mean of a set of data is not necessarily a number that is part of that set. For some students, this idea is difficult to understand.
Another way to help students develop an understanding of the concept of a mean is to ask them to identify a missing piece of data for a set of data to have a particular mean.
Example 4
Five students have been asked to fundraise. If each student raises an average of $25, the group wins tickets to a field hockey game. On Monday, four of the five students meet and find that they have raised $29, $21, $31 and $13. What is the minimum amount that Suzie, the fifth student, must have raised if the group is to win the field hockey tickets?
Students who have only learned to use the usual algorithm for determining the mean are often not able to answer this type of question. This is because it is a procedure that students are unable to adapt to the circumstances due to lack of understanding. Students who have developed an understanding of the concept of mean as an equal share are better able to solve this problem. Here is an exchange that the four students might have to determine how much money Suzie needs to have collected.
Student 1 - We need to get an average of $25, which means that if we split the money equally between us, we would each have $25. I collected $29, so I can split $4 with you.
Student 2 - I only got $21, so I am $4 short.
Student 3 - I have an extra $6 because I collected $31.
Student 4 - I'm sorry. I was sick this weekend and only raised $13. I am $12 short.
Student 1 - Let's use the idea of sharing to help us determine how much money Suzie needs to have collected.
image Under the title "Before Sharing", five boxes are lined up side by side. The first box contains 25 chips. Above it, a set of 4 chips is linked to the second box by an arrow. The second box contains 21 chips. The third box contains 25 chips, and above it, a set of 6 chips points to the fourth box with an arrow. The fourth box contains 13 chips. The fifth box contains no chips, but has a question mark.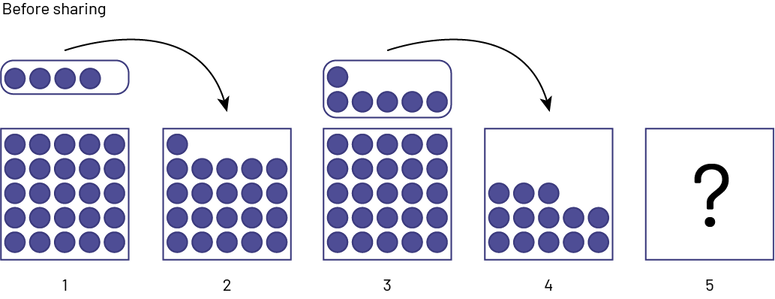
After the split, the first three students each have $25 and student 4 is $6 short of $25. Suzie must bring the missing $6 in addition to her $25. She must therefore bring in $31.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 115-121.
Knowledge: Median
The median of a set of data is the number in the middle of this ordered set such that there is an equal amount of of data values on either side. In the case of an even number of data, the median is the number that is halfway (average) between the two middle numbers. In such cases, the median may be a number that is not part of the set of data.
Example 1
The following data was recorded during a long jump competition.
1.04 m; 1.06 m; 1.12 m; 1.13 m; 1.16 m; 1.19 m; 1.22 m; 1.28 m; 1.36 m
The nine data values are in ascending order. The median of this data set is the fifth data value, which is 1.16 m. Notice that there are four data values on each side of the median.
Example 2
The stem-and-leaf plot below shows 22 numbers placed in ascending order. Two numbers are in the middle, the 11th and 12th numbers. Note that there is an equal amount of data values (10) on either side of these two middle numbers. Since the 11th and 12th values are both 72 heartbeats per minute, the median will also be 72 heartbeats per minute.
Number of Heartbeats Per Minute of Students in the Class
| 6 | 3 5 5 8 9 |
| 7 | 1 1 2 2 2 2 2 4 5 7 7 |
| 8 | 2 3 6 |
| 9 | 1 2 |
| 10 | 8 |
Example 3
At a fundraiser for their sports team, 10 students sold boxes of chocolate. Here are the numbers of boxes sold:
15, 12, 11, 10, 10, 8, 7, 6, 5, 5
This data set of 10 data values has been arranged in descending order. The 5th and 6th data values are in the centre of this set. These two data values, 10 and 8, are different. The median is 9, since 9 is halfway between 8 and 10. Despite the fact that this median is not part of the set of data, we can see that there are the same number of data values (five) on either side of it.
Example 4
Here is the data for the maximum daily temperature, in degrees Celsius, in a city in August.
| Maximum Temperatures in August | ||||||
|---|---|---|---|---|---|---|
| 17 | 20 | 19 | 25 | 27 | 28 | 30 |
| 29 | 27 | 22 | 21 | 20 | 25 | 29 |
| 32 | 33 | 33 | 27 | 24 | 17 | 21 |
| 26 | 25 | 27 | 24 | 21 | 23 | 25 |
| 16 | 18 | 19 | ||||
To determine the median students need to first arrange the values in ascending or descending order. They can use a stem and leaf plot as follows.
| 1 | 7 | 9 | 7 | 6 | 8 | 9 | ||||||||||
| 2 | 0 | 5 | 7 | 8 | 9 | 7 | 2 | 1 | 0 | 5 | 9 | 7 | 4 | 1 | 3 | 5 |
| 3 | 0 | 2 | 3 | 3 |
Students can then place the leaves in each row in ascending order and get the following diagram.
| 1 | 6 | 7 | 7 | 8 | 9 | 9 | ||||||||||
| 2 | 0 | 0 | 1 | 1 | 2 | 3 | 4 | 5 | 5 | 5 | 7 | 7 | 7 | 8 | 9 | 9 |
| 3 | 0 | 2 | 3 | 3 |
To help students determine the median, suggest that they write the numbers in order on a strip of paper and fold it.
Using the paper strip helps students develop a better understanding of the concept of median because by folding the strip in half, the numbers are paired (first to last, second to second to last, and so on) and only one piece of data is in the middle. It is then easy to see that the median of the data is 25°C.
Example 5
The graph below shows the maximum daily temperatures for a city during the month of June, in degrees Celsius.
| Daily Maximum Temperatures in June (°C) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 6 | 7 | 8 | 9 | ||||||||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 3 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 9 |
| 3 | 0 | 2 | 3 | 3 | |||||||||||||||
Have students copy the numbers from the stem-and-leaf plot onto a strip of paper. Next have the students fold the paper in half. In this case the fold should be between the two numbers in the middle, 24 and 25. Students can use their knowledge of decimal numbers to determine that it is the number 24.5 that is halfway between 24 and 25. The median of this data set is therefore 24.5 C.
The median is an important statistical measure that is commonly used in many situations. Because it indicates the value at the centre of an ordered set of data, it is possible to place all other values in relation to the median. For example, in the example of the long jump competition (Example 1), the student who successfully jumped 1.28 m knows that the length of this jump is greater than the median of 1.16 m and, therefore, greater than the length of most of the other jumps.
Before using the median to make decisions, however, it is important to consider the range of the data because the median does not take into account extreme values. Suppose that in the example about the sale of boxes of chocolate (Example 3), we are trying to approximate the number of boxes sold. We know that the median number of boxes sold is 9 and that the data range from 5 to 15 boxes. Thus, the size of the range of the data is small, and the median of 9 is almost halfway between the maximum and the minimum value. Therefore, it can be assumed that each student sold about 9 boxes and calculated that the 10 students sold about 90 boxes.
Now imagine a situation with the same data except that the maximum data is 75 boxes instead of 15 boxes. The median is still 9 boxes, but the size of the range is very large. Also, the median is not at all halfway between the maximum and minimum values, so we could not assume that each student sold about 9 boxes as in the previous situation and conclude that the 10 students sold about 90 boxes in all.
Teachers can also help students deepen their understanding of the concept of median by modifying some of the situations they have already studied, as shown in the following example.
Example 6
Let's alter Example 3 as follows:
At a fundraiser for their sports team, 10 students sold boxes of chocolate. Here are the numbers of boxes sold.
15, 12, 11, 10, 10, 8, 7, 6, 5, 5
However, three students have not yet reported their number of boxes sold. If the goal was to obtain a median number of eight boxes sold, what data set corresponding to the sales of the 13 students could meet this goal?
Here are two examples of possible answers.
15, 12, 11, 10, 10, 8, 8, 7, 7, 6, 5, 5, 4
15, 12, 11, 10, 10, 9, 8, 7, 6, 5, 5, 4, 3
If we add as a condition that the mode of the data set also corresponds to eight boxes, students could give the following answer.
15, 12, 11, 10, 10, 8, 8, 8, 7, 6, 5, 5, 4
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 111-115.