D2.1 Describe the difference between independent and dependent events, and explain how their probabilities differ, providing examples.
Skill: Explaining Why the Probabilities of Independent and Dependent Events Differ by Providing Examples
The probabilities of independent and dependent events differ, since the repetition of a dependent event reduces the total number of possible outcomes of the experiment, so the probability of an event depends on the outcome of a previous event, which is not the case for independent events.
Example
Present students with the following situation:
12 marbles of different colours are placed in a bag. There are 4 blue marbles, 3 green marbles and 5 red marbles. Using a tree diagram, determine the theoretical probabilities of drawing 2 successive red marbles for each of the following situations:
- If the first marble drawn is put back into the container;
- If the first marble drawn is kept out of the container.
Compare the two tree diagrams to distinguish between independent and dependent events.
Image Chance Tree Independent with marble return. If on the first draw there is a five out of twelve chance of drawing a red marble, and on the second draw there is a five out of twelve chance of drawing a red marble, then five out of twelve multiplied by five out of twelve equals 20 out of 144 chances of drawing two red marbles. This equation is the only one in the tree that is circled in red. If on the second draw there are three chances out of twelve to draw a green marble: five out of twelve multiplied by three out of twelve equals 15 chances out of 144 to draw a red marble and then a green marble. If on the second draw there are four chances out of twelve to draw a blue marble: five out of twelve multiplied by four out of twelve equals twenty chances out of 144 to draw a red marble then a blue marble. If on the first draw there are three chances out of twelve to draw a green marble, and on the second draw there are five chances out of twelve to draw a red marble: three out of twelve multiplied by five out of twelve equals 15 chances out of 144 to draw a green marble then a red marble. If on the second draw there are three chances out of twelve to draw a green marble: three out of twelve multiplied by three out of twelve equals nine chances out of 144 to draw two green marbles. If at the second draw there are four chances out of twelve to draw a blue marble: three out of twelve multiplied by four out of twelve equals twelve chances out of 144 to draw a green marble then a blue marble. If on the first draw there are four chances out of twelve to draw a blue marble, and on the second draw there are five chances out of twelve to draw a red marble: four out of twelve multiplied by five out of twelve equals twenty chances out of 144 to draw a blue marble then a red marble. If on the second draw there are three chances out of twelve to draw a green marble: four out of twelve multiplied by three out of twelve equals twelve chances out of 144 to draw a blue marble then a green marble. If on the second draw there are four chances out of twelve to draw a blue marble: four out of twelve multiplied by four out of twelve equals sixteen chances out of 144 to draw two blue marbles.
There are 25 favorable outcomes out of 144 possible outcomes. The probability of drawing 2 successive red marbles is 0.17 or 17%.
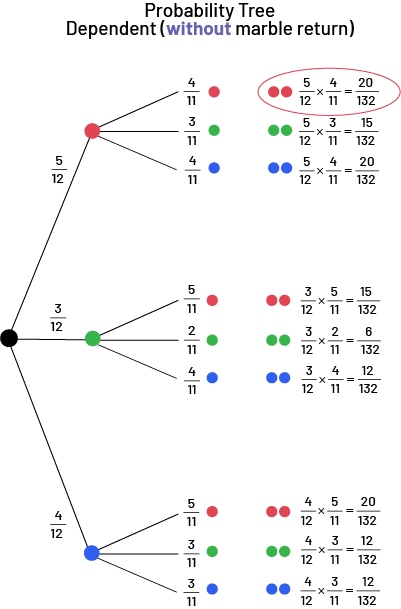Image Chance Tree Independent with marble return. If on the first draw there is a five out of twelve chance of drawing a red marble, and on the second draw there is a five out of eleven chance of drawing a red marble, then five out of twelve multiplied by five out of eleven equals 20 out of 132 chances of drawing two red marbles. This equation is the only one in the tree that is circled in red. If on the second draw there are three chances out of eleven to draw a green marble: five out of twelve multiplied by three out of eleven equals 15 chances out of 132 to draw a red marble and then a green marble. If on the second draw there are four chances out of eleven to draw a blue marble: five out of twelve multiplied by four out of eleven equals twenty chances out of 132 to draw a red marble then a blue marble. If on the first draw there are three chances out of twelve to draw a green marble, and on the second draw there are five chances out of eleven to draw a red marble: three out of twelve multiplied by five out of eleven equals 15 chances out of 132 to draw a green marble then a red marble. If on the second draw there are three chances out of eleven to draw a green marble: three out of twelve multiplied by three out of eleven equals nine chances out of 132 to draw two green marbles. If at the second draw there are four chances out of eleven to draw a blue marble: three out of twelve multiplied by four out of eleven equals twelve chances out of 132 to draw a green marble then a blue marble. If on the first draw there are four chances out of twelve to draw a blue marble, and on the second draw there are five chances out of eleven to draw a red marble: four out of twelve multiplied by five out of eleven equals twenty chances out of 132 to draw a blue marble then a red marble. If on the second draw there are three chances out of eleven to draw a green marble: four out of twelve multiplied by three out of eleven equals twelve chances out of 132 to draw a blue marble then a green marble. If on the second draw there are four chances out of eleven to draw a blue marble: four out of twelve multiplied by four out of eleven equals sixteen chances out of 132 to draw two blue marbles.
There are 20 favorable outcomes out of 132 possible outcomes. The probability of drawing 2 successive red marbles is 0.15 or 15%.
The fractions for the first draws of the two tree diagrams (independent and dependent) are identical. However, there is a difference in the fractions of the second draw in the two tree diagrams. In the tree diagram for independent events, the numerators and denominators do not change. In the tree diagram for dependent events, the numerators and denominators change on the second draw because one of the marbles is never returned to the bag.
Source: translated from En avant, les maths!, 7e année, ML, Données, p. 13-15.