F1.2 Estimate and calculate the cost of transactions involving multiple items priced in dollars and cents, including sales tax, using various strategies.
Skill: Estimating and Calculating the Cost of Transactions Involving Multiple Items (With Tax)
In the Junior Division, students deepen their understanding of how to link the strategy of rounding decimals to more accurate estimations of the value of purchased items priced in dollars and cents. Students build on prior knowledge, but specifically on the choice to round a number to the nearest tenth, one, ten, hundred, or thousand in the context of financial literacy. Students also make connections to the concept of place value.
Note that it is important to review estimation with students before asking them to calculate transaction costs. It is easy to assume that students know how to estimate, however, teaching them estimation strategies will not only help them to estimate, but also to know if their answers are reasonable when performing calculations.
Realistic learning contexts provide opportunities for students to practice using strategies to accurately calculate money amounts to the nearest cent (decimal numbers to hundredths).
Estimating and calculating costs and change in cash transactions requires the application of addition, subtraction, multiplication, division, mental math strategies, and knowledge of math facts, as illustrated in the previous section.
These types of problems support students' learning in the Number strand, specifically in developing strategies in multi-step problems involving whole numbers and decimal numbers, and in checking the reasonableness of calculations. Students also strengthen their understanding of fractional representation as percents, describing relationships and representing equivalencies between fractions, decimal numbers up to hundredths, and percents in a variety of contexts.
In the Junior Division, students will eventually add the sales tax to their total purchase. Although students have been working with fractions and proportion problems since the Primary Division, the calculation of the Harmonized Sales Tax is a concept that willneed to be further explained to them.
One way to estimate sales tax is to break it down. A common benchmark percentage is 10%. Students can determine 10% of an amount of money. Then, students can find half of 10%, or 5%, by dividing their answer in half. By adding the two numbers together,
students can estimate that the HST will be slightly less than their result.
For example, to estimate the 13% HST on $88, I take $88 and round up the HST to 15%. I break 15% down into 10% and 5%. 10% is
one-tenth, so one-tenth of $88 is $8.80. 5% of $88 is half of $8.80, or $4.40. I add these two amounts together.
\($8.80 + $4.40 = $13.20 \)
I estimate that the HST on $88 is just under $13.20.
Example
Georgina is starting her own business making reusable vegetable bags because she wants to do something positive for the environment by reducing the use of plastic. Her family thinks this is a great idea. Her family suggests that she contacts her aunt, who owns a sewing store, to get the materials she needs to make her bags. She has finished her list and needs to buy fabric for $97.99, string for $49.99, a sewing machine for $203.99, and thread for $47.50. She remembers that she also needs to include the HST. What is the total cost of her transaction?
Strategy
First of all, I round the price of each item to the nearest dollar or ten:
- fabric at $97.99 ≈ $100
- string at $49.99 ≈ $50
- $203.99 sewing machine ≈ $200
- thread at $47.50 ≈ $50.
I add up the rounded prices of the items:
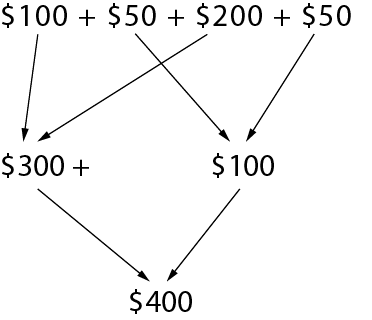
I estimate the cost of the materials for the reusable produce bags to be approximately $400. To estimate the 13% HST amount, I round up the HST to 15% of $400. I break 15% down into 10% and 5%. 10% is one-tenth, so one-tenth of $400 is $40. 5% of $400 is half of $40, or $20.
\($40 + $20 = $60 \)
I estimate that the HST for the reusable produce bag material is $60. I add that to $400, which comes to $460.
I estimate that the materials for the reusable vegetable bags including HST will cost just under $460.
Now I calculate the actual cost of the material. Since most of the prices end in $0.99, I decide to add one cent to the first three prices to get to the next dollar. I must remember to subtract that $0.03 at the end of my calculations.
Cost of materials:
- Fabric: $97.99 \(\longrightarrow\) $98
- String: $49.99 \(\longrightarrow \) $50
- Sewing machine: $203.99 \(\longrightarrow \) $204
- Thread: $47.50
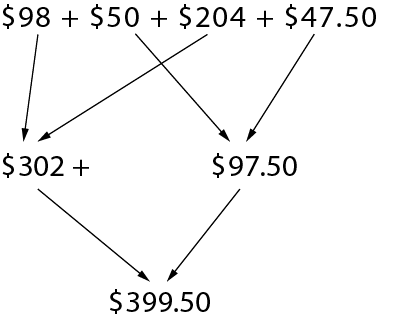
Now I have to subtract the 3 cents I added at the beginning.
\($399.50 - $0.03 = $399.47 \)
The cost of the material for the reusable veggie bags is $399.47, to which I have to add 13% HST.
I use my calculator to calculate 13% of $399.47.
\($399.47 \times 13 \% = $51.93 \)
\(399.47 + 51.93 = $451.40 \)
The total cost of the material is $451.40.
Since she is paying electronically, she will pay the correct amount of $451.40.
Knowledge: Transactions
An agreement between a buyer and a seller to exchange goods or services, including for money.
Transactions can be made through a variety of methods of payment, including cash, cheque, credit or debit card, gift card or online payment services.
Only cash transactions are rounded to the nearest multiple of 5 cents, since the penny is no longer in circulation.
Knowledge: Harmonized Sales Tax (HST)
A value-added tax levied on most goods and services sold for domestic consumption. The HST is paid by consumers but is remitted to the government by the businesses that sell the goods and services. The HST rate is 13%; this means that you have to pay $13 for every $100 of goods or services.
