General Foundations of Number
Intermediate Division
Numbers and operations play an important role in mathematics learning, as students rely on their understanding of them to master various mathematical concepts. In addition to being directly related to the other strands, numbers and operations are used daily by everyone. For this reason, the Number strand has historically been at the heart of mathematics learning.
However, learning about numbers and operations has evolved over time. The Number strand is more than:
- the application of algorithms and procedures;
- finding the right answer;
- a series of mathematical exercises.
The Number strand in the Junior Division is:
- understanding numbers and the quantities they represent;
- making connections between numerical concepts;
- the use of strategies that are understood and effective for computation in a variety of contexts.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 5.
Big Ideas
The expectations and learning content of the Mathematics Curriculum use a large number of concepts. The big ideas allow teachers to see how these concepts can be grouped together to plan more effective instructional programming.
In so doing, teachers are able to develop interrelated learning situations that enable students to:
- explore concepts in depth;
- establish links between the different concepts;
- recognize that mathematics is interrelated, not a collection of disparate pieces of knowledge.
In the sections below, the two big ideas of the Number strand are each supported by three statements. These two big ideas represent the foundations of learning in the Number strand and are discussed in relation to whole numbers, fractions and decimals, and percentages.
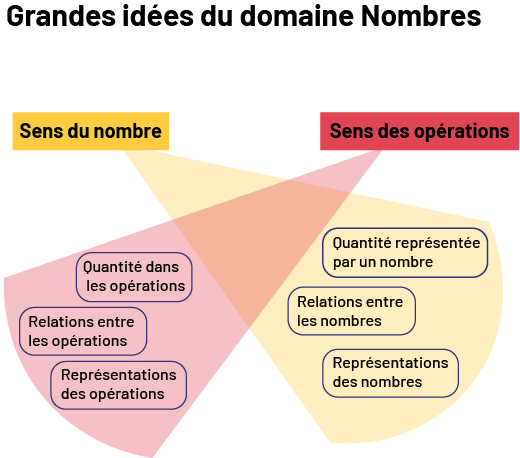
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 21-22.
The two big ideas that form the basis of the expectations for the Number strand in Grades 7 and 8 are Number Sense and Operations.Big Idea 1: Number Sense
Number sense allows us to understand the numbers around us and to treat them with discernment.
The development of students' number sense should be used as a backdrop for instruction in the Number strand. Number sense is a difficult concept to define, since it is not specific knowledge, but rather a general view of numbers. Number sense can be thought of as 'a good intuition about numbers and their relationships. It develops gradually as a result of exploring numbers, visualizing them in a variety of contexts, and relating them in ways that are not limited by traditional algorithms.' (Howden, 1989, p. 11).
In other words, number sense is the ability to recognize numbers, determine their relative values, and understand how they are used in a variety of contexts, including counting, measuring, estimating, and performing operations. It is therefore a deep relational understanding of numbers that involves many different ideas, relationships and skills.
Number sense is demonstrated or can be 'observed' while students play with numbers in a variety of mathematical situations. Students with strong number sense are aware of the importance of context in the use of numbers, can more easily estimate quantities and computations, make judgments about numbers as a result of computations, and understand their use in context. Students are able to recognize various number relationships and represent numbers flexibly.
From an early age, children count, learn to determine quantities and recognize connections between quantities and numbers, in a wide range of contexts. In the primary grades, students explore whole numbers and progress to understanding the meaning of numbers below 1000. In addition, students develop an intuition for the relative magnitude of numbers by comparing them and delving deeper into the meaning of place value. Students also have the opportunity to explore the meaning of fractions.
In the junior and intermediate grades, the development of number sense continues with the introduction of large numbers as well as various types of numbers in relation to each other. Students deepen their use of fractions and explore decimal numbers and percentages. Number sense that has been built around whole numbers is then enriched with the use of various number notations.
Number sense is a way of thinking about and seeing numbers, of being able to 'manipulate' them to grasp their meaning and use them effectively. It cannot be taught or demonstrated as such. However, for students to develop number sense, teachers must provide a variety of manipulative, exploratory, representational, construction, visualization, communication, and problem-solving activities.
Here are the statements that define Big Idea 1 - Number Sense:
Statement 1 - Quantity Represented by a Number
Understanding quantity means developing a sense of 'how many… ' or 'how many…' there are.
Statement 2 - Number Relationships
Establishing relationships means recognizing connections between numbers in order to better understand their meaning.
Statement 3 - Number Representations
Moving from one representation of a number to another allows for a better understanding of numbers.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 26-27.
Big Idea 2: Operations
Operations enable us to choose the operations to be performed and execute them efficiently according to a given situation.
Operations combine the mastery of a multitude of mathematical skills and concepts related to numbers and operations. In a given situation, it allows for numbers and operations to be used with enough flexibility and versatility to be able to perform a calculation efficiently.
Students with a well-developed sense of operations (Small, 2005 a, p. 136) understand operations and the effect they have on numbers, make connections between the properties of operations, recognize that operations are interrelated, and develop computational strategies. In addition, students can adapt these strategies to different situations and express the relationship between the context of a problem and the calculations performed. For example, students are able to explain the reason(s) behind their choice of mental calculation and justify the effectiveness of their strategy.
In the primary grades, students developed a sense of operations by working through various types of problems. These experiences allowed them to grasp concepts related to various operations (for example, multiplication can be seen as repeated addition, addition is commutative) and to develop strategies for performing operations.
In the junior and intermediate grades, students continue to develop their sense of operations by working with numbers in more complex situations and gain a better understanding of the meaning of each operation and the relationships between them. Students become increasingly comfortable with a variety of computational and problem-solving strategies, allowing them to make more informed choices in different situations. In addition, their sense of operations extends to the application of basic operations on fractions and decimal numbers.
Here are the statements that define Big Idea 2 - Operations:
Statement 1 - Quantity in Operations
Understanding operations allows one to recognize their effects on quantities.
Statement 2 - Relationships between operations
Understanding the properties of operations and the relationships between them allows for more flexible use.
Statement 3 - Representations of Operations
Knowing a variety of strategies for performing operations allows them to be used effectively in different contexts.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 72-73.
The two great ideas are both complementary and interdependent - one cannot exist without the other. Having a sense of number means understanding numbers, and what they represent. This understanding is essential to grasp what happens to numbers during operations. The goal of the Number strand is for students to use their number sense in conjunction with their understanding of operations to solve problems.
Each of the Big Ideas is explored in terms of statements with similar themes: quantity, relation, and representation. The similarity of the statements is no accident. In fact, the statements allow for the recognition of essential notions while learning how to count (understanding quantity, or 'how much'), how to recognize relationships between numbers and operations and finally, how to be flexible when representing and using numbers and operations.
The teaching of the Number strand, based on big ideas, aims to create connections and develop a more global view of numbers. Note that these big ideas and their statements are not limited to a set of numbers. For example, the fact that a number can be represented in different ways is not unique to decimal numbers, but applies to numbers in general.
All individuals need to develop a strong number sense and understanding of operations in order to solve problems. To foster this capacity among students, teachers must keep in mind the importance of these big ideas.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 24-25.
Structuring programs around big ideas and emphasizing problem solving provides students with authentic and meaningful learning situations that allow them to explore concepts in depth.
Children are better able to make connections in mathematics and therefore learn mathematics if the curriculum is structured around big ideas. Grouping expectations into big ideas facilitates student learning and teacher professional development in mathematics. Teachers will find that it is much more useful to discuss and determine the most effective instructional strategies for a big idea than to try to determine the specific strategies and approaches that would help students achieve particular expectations. The use of big ideas supports teachers to present concepts in the curriculum as interrelated, rather than isolated concepts. In order to develop a coherent math program, teachers must have a thorough knowledge of the key mathematical concepts of the grade they are teaching as well as an understanding of the connections between these concepts and the future learning of their students (Ma, 1999). This includes an understanding of the conceptual structure and fundamental skills inherent in elementary mathematics (Ma, 1999, p. xxiv) and how best to teach these concepts to children. Developing this knowledge makes teaching more effective.
Source: translated from Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 2-3.

Communication is an essential component of learning mathematics. It is a skill that goes beyond the appropriate use of mathematical terminology and symbols in verbal or written communication. It is also, more importantly, a vehicle through which students develop an understanding of mathematical concepts in contexts that involve mathematical reasoning and argumentation. This is what Radford and Demers (2004) call the conceptual dimension of communication.
These researchers also stress the importance of the social dimension of communication. Communication means exchange between two or more people. The exchange will be beneficial for all those involved, when it happens within a culture of respect, where dialogue is encouraged.
To increase the effectiveness of number instruction, teachers must foster a culture that values communication as a means of learning. This means creating opportunities for students to share their thinking and strategies. Communication is central to all learning situations.
The Role of Representations in Learning Mathematics
In mathematics, communication is not just about words. Ideas should be conveyed in different ways: concrete (for example, with rods), visual (for example, with a number line or diagram), symbolic (for example, using numerals and mathematical symbols in an equation) and, of course, verbally, using words, whether they are read, seen, said, written or heard.
These various modes of representation, shown in the diagram below, allow for multiple cognitive inputs, thereby making connections between ideas that are essential for learning. Teachers use models to represent mathematical concepts to students and students use them to solve problems, represent their thinking, and clarify their thinking.
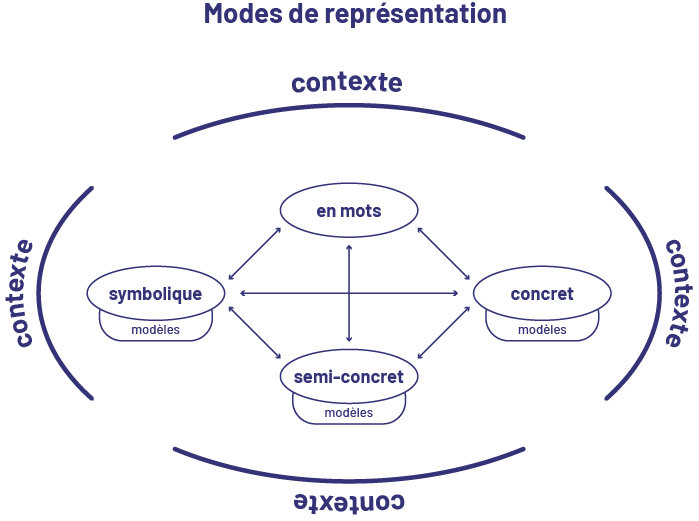
Mathematical Models
Mathematicians have long constructed models to explain and represent discoveries and observations of the world, and to communicate them effectively. For example, when thinking about a number, some people visualize it in a mathematical model such as an open number line or a number grid/chart. This helps them to better visualize the number and to recognize that it is more than, less than, or close to another number. Models are thus representations of mathematical ideas.
Young children visualize the world around them in their own way. To draw the tree in front of their house, a child will draw lines on paper and represents it in two dimensions, even though the child has touched it, walked around it and sheltered under its branches (Fosnot & Dolk, 2001, p. 74). This representation is not a copy of the tree, but a construction of what he or she knows. It is in fact a 'model' of the tree. The same is true for students whose first models used to solve problems reflect their interpretation of reality.
Fosnot and Dolk (2001, p. 80) argue that models, like big ideas and strategies, cannot be automatically transmitted, but must be constructed by students. A table of values is a good example: intuitively, students 'organize' numerical data by placing them disparately on a sheet of paper, but the table of values allows them to be ordered for processing and analysis.
It is important to recognize that the model is not the mathematical idea. Thus, the tree that the child drew in the example above is not a tree, but a representation of the situation that will be used to discuss it. The same is true for mathematical models used.
Representing a number with base ten materials is a model because it is assumed that the person using it already has an understanding of grouping. However, presenting a rod from a kit of base ten materials and claiming that it is a ten is false. The object is not a 'ten,' but a concrete way to represent the 'idea' of a ten. Here it represents a ten of small cubes, but it could represent ten things, like ten trees. Depending on what is defined as the whole it could also represent a tenth. For example, the number 2.5 can be represented with 2 flats (2 wholes) and 5 rods (5 tenths).
The number line is another model that students should have experience with. The number line does not represent the quantity of the numbers placed on it. Rather, it allows us to 'see' the numbers in relation to each other. For example, a number line with the numbers 44, 42, and 41.5 represents the order relationship between these three numbers, as well as the proportional relationships between whole numbers, halves and fourths as shown by their relative positions on the number line.

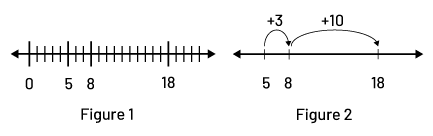
In order to foster students' reasoning, teachers should use and encourage students to use a variety of models. Models do not have to be taught formally; they can be introduced in problem-solving situations. For example, the number line is an excellent model for exploring the addition of several numbers. However, most students do not 'conceive' that it can be created without being scaled. Imagine then a mathematical exchange, in the context of an addition problem, where they present their problem-solving strategies. Teachers can use this opportunity to make a connection between the number line used by the student (Figure 1) to perform an operation and the possibility of using an open number line (Figure 2).
Example
\(\ 5 + 3 + 10\)
Similarly, in order to represent situations involving fractions, students often tend to use an area model (for example, circle or rectangle). However, this type of model does not accurately represent situations where the whole is a length or distance. Teachers can take advantage of an opportunity where students are using an area model to represent the fraction of a length and show them how a length model (for example, a number line) would be more appropriate.
Students should be exposed to a variety of representations so that they can build connections between them and consolidate their learning. Over time, students must make a transition from using a model as a tool in a particular situation to using a model as a strategy for generalizing mathematical ideas, and solving problems for a variety of new contexts. This transition from a familiar context to a new context is a fundamental step in learning mathematics. It is found in the Achievement Chart under 'Application'.
Models that students can use in the Number strand include:
- number lines;
- double open number lines;
- arrays;
- tables of values;
- number grids (for example, hundred chart);
- base ten materials;
- equations;
- area models to represent fractions;
- length models to represent fractions;
- set models to represent fractions;
- volume models to represent fractions;
- play money and base ten materials to represent decimal numbers.
Teaching Problem Solving
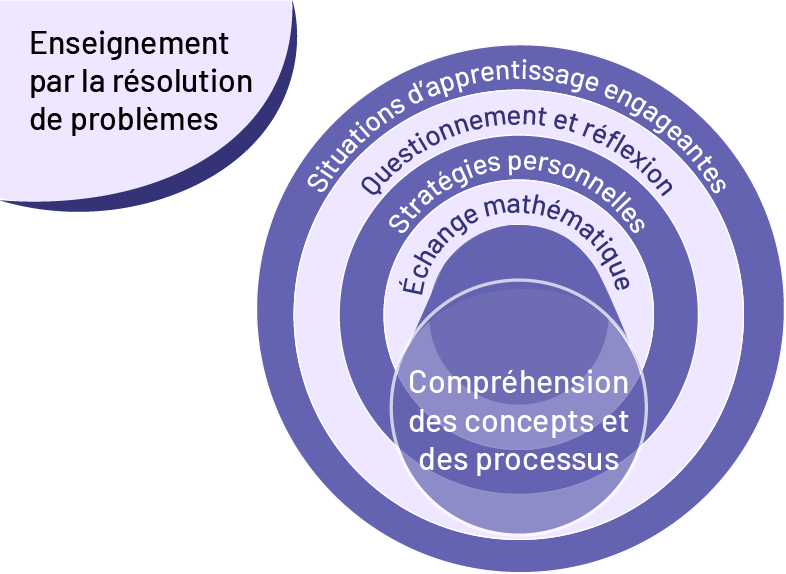
To help students fully understand the concepts and processes of the Number strand, it's important to place them in problem-solving situations right from the start of a learning unit. When they work as a team to solve an engaging, non-routine problem, students become adept at formulating a hypothesis and a mathematical argument. They also learn to take risks, persevere and have confidence in their problem-solving abilities. This is where learning mathematics really comes into its own.
Problem-based instruction requires teachers to present learning situations that sustain student interest. The context or situation of the problem then becomes a determining factor. 'Problems should be based on real contexts (situations that occur authentically in the classroom), real-life contexts (situations that are derived from experiences that could be had by students outside the classroom), and even fanciful contexts (situations that appeal to student imagination)' (Vézina et al., 2006, p. 4). Indeed, the context can be a hook for student interest and give them a reason to 'do mathematics'. Consequently, the context must be chosen, formulated and shaped judiciously in order to induce curiosity. Context, then, is an element of problem solving that can be used to engage students.
Problem-based instruction also requires that teachers present students with learning situations that are rich in mathematical content and that encourage them to think. Teachers must allow students to develop their own problem-solving strategies without overly directing them. Finally, teachers need to clarify mathematical concepts as students present their strategies and solutions during mathematical exchanges. The mathematical exchange is a mathematical conversation in which students explain and defend their thinking and analyze the thinking of others. Learning and understanding are forged through this sharing of ideas and effective questioning by the teacher. In addition, the mathematical exchange allows students to consolidate their learning and develop various skills such as problem solving, communication, reasoning, listening and analysis.
Teaching through problem solving is about understanding. In the Number strand, students will solve problems to develop a better sense of operations, which will result in the use of strategies developed through conceptual understanding rather than memorized procedures.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 13-14.

Students in the Number strand develop their knowledge and skills gradually. It is characterized by a gradual deepening of number sense and sense of operations, which takes place throughout the elementary grades.
The following tables propose a number sense development scale (Table 1) and operational sense development scale. (Table 2). Each scale describes a five-stage developmental continuum from initiation to versatility as illustrated in the diagram above.
This continuum, which reflects a path from the concrete to the abstract, is based on the following three premises.
- Students must go through all the stages for each new concept. If some of the stages are skipped, it will be difficult for them to fully develop number sense and operational sense to the multi-skill stage. However, with time and depending on their background of experiences, students will be able to move through the early stages more and more quickly.
- The journey through these stages is not exclusively unidirectional. Rather, depending on the learning situations presented, students may need to return to a previous stage to consolidate their learning.
- The stages are not disjointed. There is an intersection between consecutive stages, and student understanding can fall within this zone.
In each table, the stages are briefly defined and accompanied by a few examples of observable behaviours that serve to clarify their meaning. Teachers can use these tables as part of a diagnostic or formative assessment to determine the stage at which students are situated in relation to a particular concept. They can then plan learning situations that correspond to student development, enabling them to move on to the next stage. Progression from one stage to the next depends on the relevance of learning activities and mathematical exchanges in the classroom. In other words, the more meaningful experiences students have, the sharper and clearer their understanding will be.
Note: It is important to note that the five stages in the two tables are not related in any way to the grades or achievement levels in the Mathematics Curriculum rubric.
Table 1 below describes the stages of number sense development. It is important to remember that the word number in this table includes whole numbers, fractions, and decimal numbers. When a set of numbers is the object of study for the first time, students are usually in Stage 1. For example, when studying decimal numbers in Grade 4, students are at Stage 1 for that set of numbers. However, students may be at Stage 3 for whole numbers.
Table 1 - Number Sense Development
|
Step |
Examples of Observable Behaviours |
|---|---|
|
Stage 1 - Initiation Intuitive understanding of the quantity represented by certain numbers |
The student:
|
|
Stage 2 - Concrete Representation Ability to represent numbers in a concrete way |
The student:
|
|
Stage 3 - Formalization Understanding of the quantity represented by numbers and the symbolic representations equivalent to that quantity |
The student:
|
|
Stage 4 - Consolidation Ability to use number relationships in a variety of situations |
The student:
|
|
Stage 5 - Flexibility Ability to manipulate numbers with flexibility |
We are learning to:
|
The following Table 2 describes the stages of development of operational sense. It is important to link operational sense to the set of numbers with which students perform operations. For example, a student may be able to perform basic operations with fractions using concrete materials (stage 2) while being able to perform basic operations with natural numbers using personal strategies (stage 3). The progression from one stage to the next can also be done at a different pace depending on the operations. For example, the student may be at step 4 with the operations of addition and subtraction of natural numbers, but at step 3 with the operations of multiplication and division of these same numbers.
Table 2 - Operational Sense Development
|
Step |
Examples of Observable Behaviours |
|---|---|
|
Stage 1 - Initiation Intuitive understanding of the meaning of operations |
The student:
|
|
Stage 2 - Concrete Representation Ability to represent numbers in a concrete way |
The student:
|
|
Stage 3 - Formalization Ability to perform operations using personal strategies and standard algorithms |
The student:
|
|
Stage 4 - Consolidation Ability to use operations effectively in a variety of situations |
The student:
|
|
Stage 5 - Flexibility Ability to use operations flexibly |
The student:
|
In the primary grades, students generally develop an understanding of whole numbers and the four basic operations without fully grasping the complexity of these concepts. The development of number sense and operational sense continues in the junior and Intermediate Divisions with the study of large whole numbers, fractions and decimals.
By the end of the junior grades, students will not have reached the multi-skill stage for all number or operations concepts. Progression continues in Grades 7 and 8, particularly in fractions, ratios and decimals. The long-term goal for teachers is to consolidate students' understanding and develop flexibility in the use of numbers and operations.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 15-20.
