GEEM

General Foundations of Number

Primary Division

In developing a mathematics program, it is important to focus on the main mathematical concepts, or 'big ideas,' and the knowledge and skills that relate to them.

Big ideas provide teachers with a global vision of the concepts being studied and support them to :

make decisions about teaching (for example, deciding whether to emphasize a lesson or a set of lessons);
determine students' prior knowledge;
establish a link between the student's thinking and understanding of mathematical concepts (for example, strategies used by students when counting);
gather observations and make anecdotal reports;
provide feedback to students;
determine the next steps in the learning process;
communicate concepts and an assessment of their students' performance to parents (for example, by including comments in the report card).

Therefore, it is important that teachers focus their instruction on the big mathematical ideas. Grouping expectations around a few big ideas helps to foster a deeper understanding of mathematics.

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 2-3.

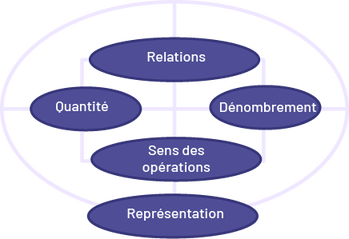
To support teachers using Big Ideas in their teaching and assessment of mathematics, this section discusses five that are important to primary years.

Big Idea 1: Counting

Counting requires the ability to count, recognize symbols, and understand the relationships between numbers and quantities.

Big Idea 2: Operations

Grasping the meaning of and relationships between operations requires understanding the concepts and procedures involved in mathematical operations.

Big Idea 3: Quantity

To quantify means to associate a number with what can be counted or measured.

Big Idea 4: Relationships

Studying relationships among numbers leads to recognizing patterns and making important connections.

Big Idea 5: Representation

Representing a number using manipulatives (concrete), visuals (sketches or diagrams), and symbols involves the concepts of number, quantity, term and place value.

These big, overlapping ideas are conceptually interdependent and equally important. For example, counting requires an understanding that the result of a count represents a quantity that can be represented symbolically. Being able to connect this knowledge to the relationships that characterize the base ten place value system provides students with a solid foundation for developing their number sense. The three big ideas of counting, quantity, and relationships impact the big idea operations as it relates to the actions of mathematics. Representations used in mathematics can be concrete (for example, manipulatives), pictorial (for example, drawings, diagrams, graphs) or symbolic (for example, numerical, algorithms, and other notations used for decimal numbers and fractions.)

The following section describes the underlying statements for each of the big ideas in the Number strand from Grades 1 to 3.

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 5-6.

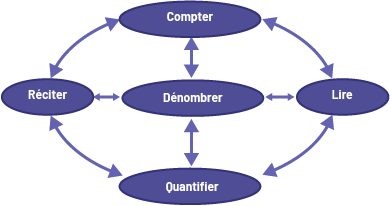
Big Idea: Counting

Overview of the Big Idea

Many of the mathematical concepts that students learn in the early grades are closely related to counting. Students' ability to count and the variety and accuracy of the counting strategies they use are good indicators of their mathematical understanding and progress.

Important considerations about counting in the early grades include:

Counting involves both reciting a sequence of numbers and associating them with a series of objects.
Counting involves being able to relate a quantity to the name or number symbol (numeral) that represents it.
Developing a conceptual understanding of ordered counting has a direct link to understanding quantity, place value, and operations.

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 9-10.

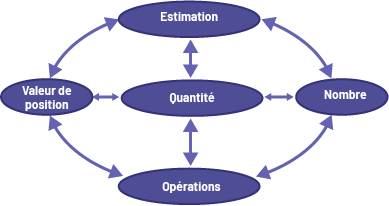
Big Idea: Quantity

Overview of the Big Idea

Children discover the concept of quantity long before they enter school. For example, they can tell which object is bigger or smaller than another, whether two quantities are the same, or whether one quantity is larger than another. Even toddlers can tell the difference between a whole cookie and half a cookie, and express their preference. However, having a preliminary sense of quantity does not mean being able to count. Over time, children make some connections between the words used to count and the quantities those words represent but may not intuitively understand the relationship between a number and the quantity it represents.

Important considerations about quantity in the early grades include:

To quantify means to associate a number with what can be counted or measured.
A quantity describes an order of magnitude (the 'number of' or 'how many there are') and is an essential concept in developing number sense.
It is important to grasp the concept of quantity in order to understand the concept of place value, operations, and fractions.
An understanding of the concept of quantity enables students to estimate and manipulate numbers.

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 43-44.

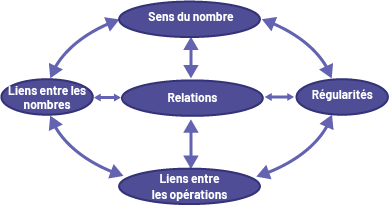
Big Idea: Relationships

Overview of the Big Idea

A clear understanding of the relationships that exist between numbers enables students to make important connections in mathematics and provides a solid foundation for learning basic operations and developing number sense. Students discover relationships by exploring the patterns found in various number sequences. For example, in the number sequence 2, 4, 6, 8, 10…, they observe that each even number is 2 more than the previous one. Students who have a good grasp of the relationships between numbers from 1 to 10 can more easily make transfers (for example, the difference between 1 and 5 is the same as between 21 and 25). Students can discover all kinds of number relationships using a number grid, number line, or calendar. The ability to recognize these relationships is important throughout elementary mathematics (for example, connections between basic operations, connections between rational numbers and between negative integers).

Making connections between numbers means recognizing and using the patterns among numbers.

Recognizing and understanding the patterns in a set of numbers promotes making connections between these numbers.
Making connections between numbers supports comparing and ordering them, and meaning-making.
Exploring the relationships between basic operations supports understanding and using them.
Knowing the benchmarks 5 and 10 and how they relate to other numbers makes it easier to understand place value and use operations.

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 59-60.

Big Idea: Representation

Overview of the Big Idea

A number is an abstract representation of a very complex concept. Numbers are most often represented either by a sequence of alphabetic symbols (for example, fifteen) or by a sequence of numeric symbols (15). They are used in a variety of contexts, and it is often the context that specifies the 'meaning' of the number. Consider, for example, the different uses of numbers in the following sentence: ‘John, who is in Grade 1, is inviting 15 children to his 7th birthday party on January 5, 2004 at 2pm.’ Understanding the meaning of different representations and uses of numbers is fundamental to the development of number sense.

Symbolically representing a number implies grasping the concepts of number, quantity, term and place value.

Representing a number implies knowing how to read and write it in letters and numbers, and being able to move easily from one representation to the other.
The symbolic form of a number represents either its name, a quantity of objects, or a pattern within a structure. The value of each of the digits that make up the number depends on the position it occupies in the number (for example, the digit 1 in a three-digit number can mean 1, 10, or 100 depending on its position).
Grasping the connections between the symbolic representations of numbers (including fractions and decimals) and the quantities they stand for is essential to the development of number sense.

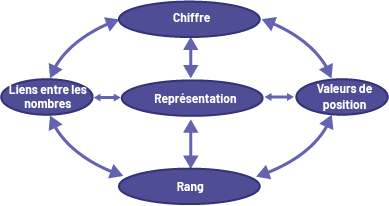
Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 71-72.

Big Idea: Operations

Overview of the Big Idea

Students need to understand the concepts and procedures involved in mathematical operations. A study (Ma, 1999) of teaching methods for operations revealed that teachers tend to emphasize the procedural dimension of operations and pay little attention to the underlying concepts (for example, number decomposition, place value) or to the connections between operations (subtraction is the inverse operation of addition).

By placing more emphasis on the underlying concepts, teachers help their students understand how numbers and operations are related.

To acquire these concepts, students must have multiple opportunities to represent problem-solving situations with manipulatives, create their own algorithms, and estimate the outcome of addition, subtraction, multiplication, and division before using and memorizing common algorithms.

Grasping the meaning of operations requires understanding the concepts and procedures involved in operations.

Developing and using strategies related to enumeration, place value, and decomposition enables students to perform operations effectively.
Students become aware of patterns in number sequences generated by operations using number lines, number grids/charts and manipulatives.
Understanding the connections between operations (for example, addition and subtraction are inverse operations) helps students learn basic number facts and solve problems.
Students gain operational awareness by developing and using algorithms in real-world problem-solving situations.

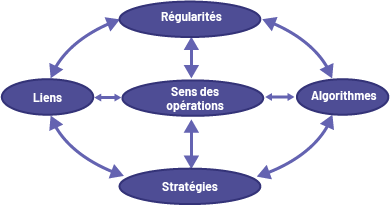
Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 25-26.

There are many teaching principles that apply across the early grades in all areas and support the teaching of big ideas in mathematics, including:

Oral communication between students is fundamental.

Students need to talk about mathematical concepts and their understanding of them, either with other students or with a teacher.

A variety of conceptual representations promotes understanding and communication.

Concepts can be represented in a variety of ways (for example, using manipulatives, visually, or with symbols). Students who use manipulatives or visuals (sketches or diagrams) to represent a mathematical concept are more likely to master it. Student attitudes towards mathematics improve when teachers use manipulatives to teach concepts that are more difficult to grasp (Sowell, 1989; Thomson and Lambdin, 1994). However, students need to be supported in their use of concrete visual representations in order to make connections between the mathematical concept and the symbols and language used to represent it.

Problem solving is fundamental to learning and doing mathematics.

Problem-solving situations provide interesting and motivating contexts for students to understand the relevance of this discipline to everyday life. Even very young children benefit from this learning context. It is much more valuable for children to learn the basics in a relevant, concrete problem-solving context than to memorize procedures without a specific purpose.

Students should have many experiences using a variety of resources and learning strategies (for example, number strips, number lines, number grids or mats, base ten materials, linking cubes, ten frames, calculators, math games, math songs, physical movements, math stories).

Some strategies (such as using math songs or movement) are not directly problem-solving activities; nevertheless, they are very useful because they respond to the learning styles of many children, especially in the early grades.

When faced with concepts of increasing complexity, students must be encouraged to use their reasoning skills.

It is important that mathematics be meaningful to students and students have the skills required to approach mathematical problems and calculations. Teachers should encourage students to apply their reasoning skills by helping them:

identify patterns: Students should be offered various experiences in which they are supported to notice that the base ten numbering system and the actions numbers (operations) are based on patterns;
estimate: Students who learn to estimate can determine if their answer is reasonable. In learning to estimate, the student should be encouraged to develop benchmarks or known quantities (for example, 'This is what a jar with 10 cubes and a jar with 50 cubes look like. How many cubes do you think are in this one?').

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 7-8.

Structuring programs around big ideas and emphasizing problem solving provides students with authentic and meaningful learning situations that allow them to explore concepts in depth.

Children are better able to make connections in mathematics and therefore learn mathematics if the curriculum is structured around big ideas. Grouping expectations into big ideas facilitates student learning and teacher professional development in mathematics. Teachers will find that it is much more useful to discuss and determine the most effective instructional strategies for a big idea than to try to determine the specific strategies and approaches that would help students achieve particular expectations. The use of big ideas supports teachers to present concepts in the curriculum as interrelated, rather than isolated concepts. In order to develop a coherent math program, teachers must have a thorough knowledge of the key mathematical concepts of the grade they are teaching as well as an understanding of the connections between these concepts and the future learning of their students (Ma, 1999). This includes an understanding of the conceptual structure and fundamental skills inherent in elementary mathematics (Ma, 1999, p. xxiv) and how best to teach these concepts to children. Developing this knowledge makes teaching more effective.

Source: translated from Guide d'enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 2-3.

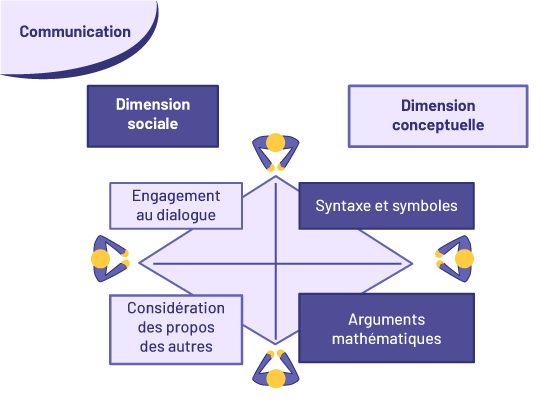
Communication is an essential component of learning mathematics. It is a skill that goes beyond the appropriate use of mathematical terminology and symbols in verbal or written communication. It is also, more importantly, a vehicle through which students develop an understanding of mathematical concepts in contexts that involve mathematical reasoning and argumentation. This is what Radford and Demers (2004) call the conceptual dimension of communication.

These researchers also stress the importance of the social dimension of communication. Communication means exchange between two or more people. The exchange will be beneficial for all those involved, when it happens within a culture of respect, where dialogue is encouraged.

To increase the effectiveness of number instruction, teachers must foster a culture that values communication as a means of learning. This means creating opportunities for students to share their thinking and strategies. Communication is central to all learning situations.

The Role of Representations in Learning Mathematics

In mathematics, communication is not just about words. Ideas should be conveyed in different ways: concrete (for example, with rods), visual (for example, with a number line or diagram), symbolic (for example, using numerals and mathematical symbols in an equation) and, of course, verbally, using words, whether they are read, seen, said, written or heard.

These various modes of representation, shown in the diagram below, allow for multiple cognitive inputs, thereby making connections between ideas that are essential for learning. Teachers use models to represent mathematical concepts to students and students use them to solve problems, represent their thinking, and clarify their thinking.

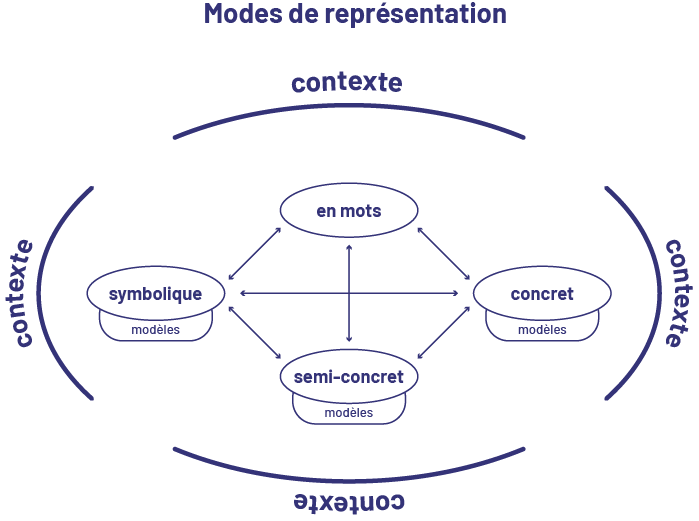
Mathematical Models

Mathematicians have long constructed models to explain and represent discoveries and observations of the world, and to communicate them effectively. For example, when thinking about a number, some people visualize it in a mathematical model such as an open number line or a number grid/chart. This helps them to better visualize the number and to recognize that it is more than, less than, or close to another number. Models are thus representations of mathematical ideas.

Young children visualize the world around them in their own way. To draw the tree in front of their house, a child will draw lines on paper and represents it in two dimensions, even though the child has touched it, walked around it and sheltered under its branches (Fosnot & Dolk, 2001, p. 74). This representation is not a copy of the tree, but a construction of what he or she knows. It is in fact a 'model' of the tree. The same is true for students whose first models used to solve problems reflect their interpretation of reality.

Fosnot and Dolk (2001, p. 80) argue that models, like big ideas and strategies, cannot be automatically transmitted, but must be constructed by students. A table of values is a good example: intuitively, students 'organize' numerical data by placing them disparately on a sheet of paper, but the table of values allows them to be ordered for processing and analysis.

It is important to recognize that the model is not the mathematical idea. Thus, the tree that the child drew in the example above is not a tree, but a representation of the situation that will be used to discuss it. The same is true for mathematical models used.

Representing a number with base ten materials is a model because it is assumed that the person using it already has an understanding of grouping. However, presenting a rod from a kit of base ten materials and claiming that it is a ten is false. The object is not a 'ten,' but a concrete way to represent the 'idea' of a ten. Here it represents a ten of small cubes, but it could represent ten things, like ten trees. Depending on what is defined as the whole it could also represent a tenth. For example, the number 2.5 can be represented with 2 flats (2 wholes) and 5 rods (5 tenths).

The number line is another model that students should have experience with. The number line does not represent the quantity of the numbers placed on it. Rather, it allows us to 'see' the numbers in relation to each other. For example, a number line with the numbers 44, 42, and 41.5 represents the order relationship between these three numbers, as well as the proportional relationships between whole numbers, halves and fourths as shown by their relative positions on the number line.

In order to foster students' reasoning, teachers should use and encourage students to use a variety of models. Models do not have to be taught formally; they can be introduced in problem-solving situations. For example, the number line is an excellent model for exploring the addition of several numbers. However, most students do not 'conceive' that it can be created without being scaled. Imagine then a mathematical exchange, in the context of an addition problem, where they present their problem-solving strategies. Teachers can use this opportunity to make a connection between the number line used by the student (Figure 1) to perform an operation and the possibility of using an open number line (Figure 2).

Example

\(\ 5 + 3 + 10\)

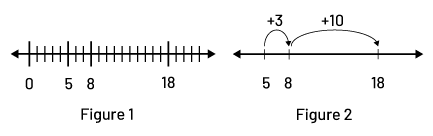
Similarly, in order to represent situations involving fractions, students often tend to use an area model (for example, circle or rectangle). However, this type of model does not accurately represent situations where the whole is a length or distance. Teachers can take advantage of an opportunity where students are using an area model to represent the fraction of a length and show them how a length model (for example, a number line) would be more appropriate.

Students should be exposed to a variety of representations so that they can build connections between them and consolidate their learning. Over time, students must make a transition from using a model as a tool in a particular situation to using a model as a strategy for generalizing mathematical ideas, and solving problems for a variety of new contexts. This transition from a familiar context to a new context is a fundamental step in learning mathematics. It is found in the Achievement Chart under 'Application'.

Models that students can use in the Number strand include:

number lines;
double open number lines;
arrays;
tables of values;
number grids (for example, hundred chart);
base ten materials;
equations;
area models to represent fractions;
length models to represent fractions;
set models to represent fractions;
volume models to represent fractions;
play money and base ten materials to represent decimal numbers.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 8-12.

Teaching Problem Solving

To help students fully understand the concepts and processes of the Number strand, it's important to place them in problem-solving situations right from the start of a learning unit. When they work as a team to solve an engaging, non-routine problem, students become adept at formulating a hypothesis and a mathematical argument. They also learn to take risks, persevere and have confidence in their problem-solving abilities. This is where learning mathematics really comes into its own.

Problem-based instruction requires teachers to present learning situations that sustain student interest. The context or situation of the problem then becomes a determining factor. 'Problems should be based on real contexts (situations that occur authentically in the classroom), real-life contexts (situations that are derived from experiences that could be had by students outside the classroom), and even fanciful contexts (situations that appeal to student imagination)' (Vézina et al., 2006, p. 4). Indeed, the context can be a hook for student interest and give them a reason to 'do mathematics'. Consequently, the context must be chosen, formulated and shaped judiciously in order to induce curiosity. Context, then, is an element of problem solving that can be used to engage students.

Problem-based instruction also requires that teachers present students with learning situations that are rich in mathematical content and that encourage them to think. Teachers must allow students to develop their own problem-solving strategies without overly directing them. Finally, teachers need to clarify mathematical concepts as students present their strategies and solutions during mathematical exchanges. The mathematical exchange is a mathematical conversation in which students explain and defend their thinking and analyze the thinking of others. Learning and understanding are forged through this sharing of ideas and effective questioning by the teacher. In addition, the mathematical exchange allows students to consolidate their learning and develop various skills such as problem solving, communication, reasoning, listening and analysis.

Teaching through problem solving is about understanding. In the Number strand, students will solve problems to develop a better sense of operations, which will result in the use of strategies developed through conceptual understanding rather than memorized procedures.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 13-14.