B1.1 Read and represent whole numbers up to and including 50, and describe various ways they are used in everyday life.
Skill: Reading Whole Numbers
Reading numbers helps to interpret them as quantities when they are expressed in words or numbers, or represented using concrete materials or models.
A quantity describes an order of magnitude (the "number of" or "how many there are") and is an essential concept in developing number sense.
When very young children are learning to count, they do not immediately make connections between the numbers recited and the notion of quantity. Students mechanically associate each number, 1,2,3,4,5, with each object in a given set. While doing this, students do not necessarily grasp that the number 5 also corresponds to the quantity of objects in the set. The link between the quantity and the number that represents it is very complex. The same number can describe very different realities. For example, the number 2 can represent 2 apples, 2 loaves of bread or 1 apple and 1 loaf of bread. It can represent 2 big balloons as well as 2 small balloons. Thus, even if the sets of objects are different, the quantity of objects in each set is the same. The complexity is increased when the quantity refers to a measurement, such as length, mass, and capacity, since the "quantified objects," i.e., units of measurement (for example, cm, kg, or mL), are not manipulatable in the same way that, for example, apples, breads, or balloons are.
The concept of quantity is important for understanding the concept of place value.
The concept of quantity is involved in understanding place value of the digits that make up a number. This value increases successively by a factor of 10 when the digits are read from right to left and decreases by a factor of 10 when they are read from left to right. Understanding the concept of place value is also very helpful when students begin to use larger numbers or decimal numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 44.
Developing a conceptual understanding of counting has a direct link to understanding quantity and place value.
By counting in concrete activities, students acquire the basic concepts and strategies that help them understand the quantitative value of number. They learn to count accurately, to recognize patterns in the base ten number system (11, 12, 13…; 21, 22, 23…; 31, 32, 33…), and to relate these patterns to the place value of the digits that make up the numbers. Teachers must take into account that some numbers are particularly difficult to learn in English. For example, consider a number like 12, which students will spontaneously call "ten-two or two-teen.
Example 1
Help students learn the names of numbers 11-19 and recognize that they do not follow the regularity of numbers 20-49 (for example, twenty-one, thirty-one, forty-one). Point out that the numbers 11-19 are formed from the numbers 1-9 and that some begin with the same letters (two and twelve; three and thirteen; four and fourteen; six and sixteen) while eleven is different.
Example 2
Help students identify patterns in a number grid such as:
- The number 9 always ends the decade (29, 39, 49, for example).
- In the pattern 10, 20, 30…, the tens digit follows the same pattern as 1, 2, 3…
- The pattern of numbers within each ten is formed from 1, 2, 3… (20 combines with 1 to become 21, then with 2 to become 22, and so on).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 12.
Underlying Elements
According to the most recent educational literature, the following are considered to be foundations for the development of the concept of quantity.
Conservation Principle
Piaget's (1965) work with young children revealed that they had a false conception of quantity. In one experiment, tokens on a table were moved away from each other, and the children were asked to say whether the quantity remained the same or was different. They responded that there were now more tokens, demonstrating their lack of understanding of the concept of conservation of number, that the quantity remains constant even if the elements are scattered to give the impression of a larger quantity. On the other hand, students who have grasped this concept understand that a quantity of objects can only be changed by adding or subtracting elements.
To determine if a student understands the conservation principle, ask: Which row contains the most objects?

Subitizing
The ability to subitize, or identify a quantity globally is the ability to quantify the elements of a given set of objects without counting. Activities designed to develop this skill (using dot cards, for example) help students develop a mental representation of the quantity associated with a number.
Dot Cards:
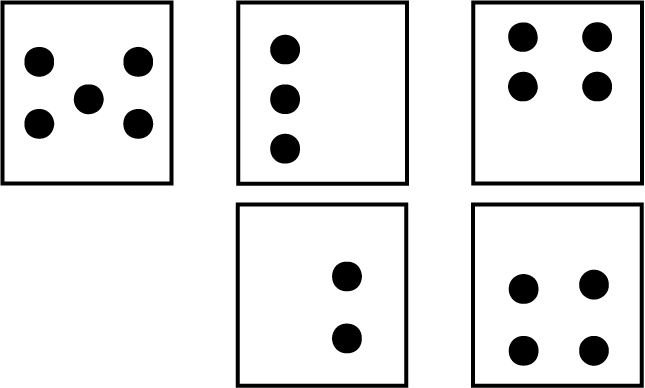
Relationships to the Anchor of 5 and 10 (Friendly Numbers)
Students gain a better grasp of the meaning of quantity by thinking of some numbers in terms of an anchor such as the number 5 or the number 10; for example, 2 is 3 less than 5 in a five frame. Recalling groupings that result in 10, such as 6 + 4 or 7 + 3, or recognizing that some numbers may represent a grouping of 10 and another number, such as 12, which is the result of 10 + 2, is helpful in deepening number sense.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 45-47.
Knowing the anchor points or friendly numbers 5 and 10 and their relationship to other numbers facilitates understanding of place value. Students become aware of number relationships as soon as they begin to count on their fingers. At this point, students discover the relationships between the numbers 1 to 4 and the number 5, and the numbers 1 to 9 and the number 10. Understanding these relationships helps them recognize, for example, that in a ten frame, where counters have been placed on all but one square, the number 9 has been represented. This understanding is later extended, first to the relationships between the numbers 0 to 10 and the anchor points 5 and 10, and then to larger numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 63.
Skill: Representing Whole Numbers
Representing a number involves knowing how to read and write it using letters and numerals, and how to move easily from one representation to another.
In the early years of school, an important aspect of representation is learning how to read and write numerals and connect numerals with the written and spoken words for numbers and with the concepts they represent.
Young children need to master writing the numbers 0 to 9. To do this, Baroody (1997) suggests helping children recognize the characteristics of each number; for example, 1 looks like a stick; 9 looks like a balloon on the end of a stick. It is also important that students practice writing numbers during interesting and motivating contexts, such as simulating grocery shopping, rather than in a repetitive practice setting. This skill also involves being able to use different visuals (ten frame or other manipulatives) and different media (tactile materials, paint, playdough, collage, chalk, grid) to represent the number.
Making connections between the symbolic representation of numbers and the quantity they represent is essential to the development of number sense.
In the early grades, many students have difficulty understanding that the quantity represented by a numeral is connected to its place value.
Example
For example, students were asked to count 26 cubes. When asked to write down the number of cubes, the students were able to write 26. When asked to point to the cubes that represented the ones digit (6), students were able to do so. However, when asked to show the cubes that represented the tens digit (2), students showed 2 cubes, without being able to explain why there were so many cubes left.
It is therefore important to provide students with many activities involving decomposing numbers into tens and ones to help them grasp the concept of quantity related to place value.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 72-73.
Skill: Describing the Ways in Which Numbers are Used in Everyday Life
To understand the concept of the number 4, one must make connections between the numeral, 4, the word, four, the quantity of 4 things, or the position in a sequence, such as the fourth desk in a row. Numbers are also sometimes used as a name or label, without reference to quantity or position; for example, 4 in a telephone number or on a soccer jersey. Adults, who have long understood that the meaning of numbers depends on the context in which they are used, are often unaware of the difficulty that students may have in understanding these differences.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 73.
Knowledge: Whole Numbers
A positive number, including zero, that has no decimal or fractional parts; for example, 0, 1, 2, 3, 4, 5, ....…}.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
