B2.1 Use the properties of addition and subtraction, and the relationship between addition and subtraction, to solve problems and check calculations.
Skill: Using the Properties of Addition and Subtraction to Solve Problems and Check the Reasonableness of Calculations
"Using the properties of operations and the relationships between operations allows us to construct numerical sentences and manipulate them flexibly in ways that solve equations and simplify calculations." [translation]
(Department of Education and Training of Western Australia, 2005, p. 66)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 97.
It is not necessary for elementary students to know the names of the properties. They just need to use them naturally to combine numbers.
Students demonstrate their understanding of the properties of mathematical operations with specific objects or numbers. Students use concrete materials, drawings, words, or symbols to represent mathematical ideas and relationships.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 17.
The properties of addition are:
- commutative property (for example, 1 + 2 = 2 + 1
- additive zero property (adding zero leaves the original quantity unchanged) (for example, 1 + 0 = 1 and 0 + 1 = 1).
The property of subtraction is :
- the zero property for subtraction (for example, 1 - 0 = 1).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 33.
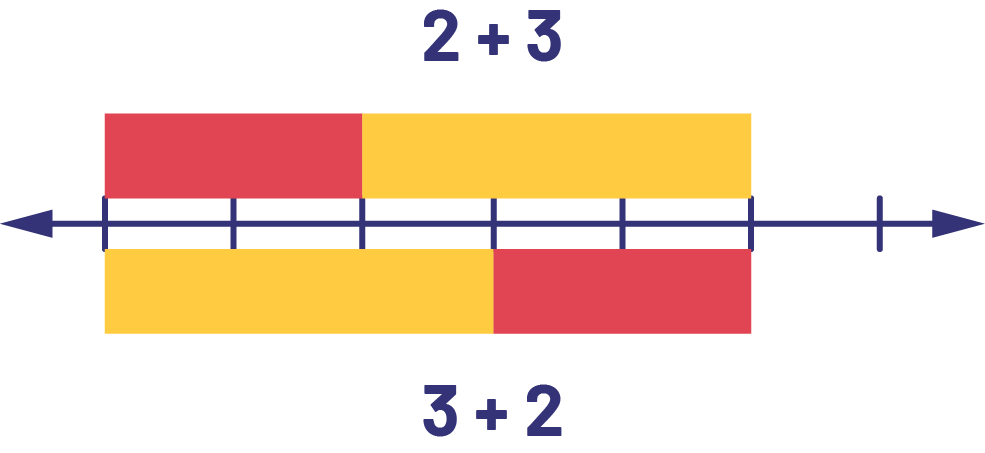
Commutative Property
Students who recognize the commutative property of addition can cut however many number facts they need to learn in half. Visual representation of facts such as 3 + 2 and 2 + 3 helps students grasp this relationship.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 19.
Zero Property (Property of the Number 0 in Addition and Subtraction)
When using the zero property in addition, teachers encourage students to propose conjectures such as, "If I add 0 to a quantity (for example, 5 + 0), that quantity stays the same, and if I add any quantity to 0 (for example, 0 + 5), I get the added quantity."
By applying these conjectures to different numbers, students will be able to formulate a generalization that this property of the number 0 is true for all numbers.
For the identity rule in subtraction, teachers encourage students to propose a conjecture such as, "When I subtract 0 from a number (for example, \(5 - 0\)), I get the starting number." By applying this conjecture to different numbers, students will be able to formulate a generalization that this property of the number 0 is true for all numbers.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 93 et 95.
Skill: Using the Relationship Between Addition and Subtraction to Solve Problems and Check the Reasonableness of Calculations
Relationship Between Addition and Subtraction
Understanding the connections between operations (for example, addition and subtraction are inverse operations) helps students learn basic number facts and solve problems.
Source: Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.
Addition and subtraction are inverse operations. When students are learning, they often have difficulty solving equations such as 17 + Mathord = 31. Teachers then encourage their students to use the inverse operation, subtraction. This can be a learning trick unless students understand why subtraction is a possible strategy.
Students must first grasp the relationship of the whole and its parts, and the meaning of a difference. For example, a number can be represented as follows:
This way of representing the relationship between a number and its parts allows us to see that subtraction is the inverse operation of addition. Thus, since 10 + 8 = 18 and 8 + 10 = 18, then 18 - 10 = 8 and 18 - 8 = 10. In addition, students can see that addition is commutative (10 + 8 = 8 + 10) and that subtraction is not (18 - 10 ≠ 18 - 8). Those who have developed good number sense and are able to decompose and group numbers can use their knowledge to more effectively solve equations such as \(10 + \mathord{?} = 18\) by understanding that we are looking for the difference between 10 and 18.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97-98.
Knowledge: Properties of Operations
Properties of operations are characteristics that are unique to operations, regardless of the numbers involved; for example, addition is commutative since 3 + 5 = 5 + 3 = 8, 4 + 7 = 7 + 4 = 11.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 102.
Knowledge: Commutative Property
The Commutative Property is explained by the fact that the result of an operation does not change when the order of the terms that make it up is interchanged. Addition is commutative. Subtraction is not commutative because the result of the first operation is greater than zero, and the result of the second is less than zero.
Example
\(\ 2 + 3 = 3 + 2\)
\(\ 6 - 3 ≠ 3 - 6 \)
Source : adapted from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 102.
Knowledge: The Identity Property
The identity property occurs when a number is combined with a special number (identity element) by using one of the operations, and the result leaves the original number unchanged. In addition, and subtraction, the identity element is 0; for example, for example, 7 + 0 = 7 and 0 + 7 = 7.
In a subtraction, the number 0 has no effect only when it is the second term (for example, (3 - 0 = 3)).
Source : The Ontario Curriculum, Mathematics, Grades 1-8, Ontario Ministry of Education, 2020.