B2.4 Use objects, diagrams, and equations to represent, describe, and solve situations involving addition and subtraction of whole numbers that add up to no more than 50.
Skill: Representing, Describing and Solving Situations
In addition to teaching arithmetic operations using strategies and reasoning, it is important to introduce these operations in problem-solving contexts. In problem solving, students are encouraged to use prior knowledge and make connections to new learning. These connections can be broken if students are not presented with a diverse range of problems. Students who do not learn to calculate in problem-solving contexts may have great difficulty making these connections later. Their understanding of the abstract concept of number and its application may be blurred, and some students may not be able to effectively use computational strategies to solve problems.
The use of problem-solving contexts is equally important for multi-digit number operations. When students are given problems, when they are encouraged to come up with an algorithm and use it flexibly, they are given the opportunity to deepen their understanding of operations. In the interest of efficiency and in the belief that it is the right thing to do, students are often taught the algorithm to be used to perform operations on multi-digit numbers. With this method presented as the "right way" to solve the problem, students struggle to understand and remember this procedure. This method often results in inefficient use of the algorithm, lack of accuracy, and limited understanding. If, instead, students are encouraged to make sense of the problem and develop their own strategies for solving it, they will show more fluency and accuracy in their work with operations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 5.
In this regard, the use of written problems, namely, problems presented in the form of statements, is one of the most effective strategies for understanding operations and thus helping students to progress in understanding problems.
Written Problems Involving Addition and Subtraction
Students develop an understanding of addition and subtraction and number relationships by solving written problems. Faced with a problem like this one: Pascale has some marbles; someone gives her 3 more and she now has 8. How many did Pascale have originally? Note that while the adult may not see any difficulty in solving this type of problem, the child does. By using modelling to represent the problem and then attaching an operation to it, teachers help students make connections between conceptual understanding and procedural mastery in problems of varying degrees of complexity.
The following types of problems presented with examples can help students perceive basic addition and subtraction number facts in a variety of ways: joining problems, seperating problems, part-part-whole problems and comparing problems. Using problems to introduce basic number facts forces students to reason their way to solutions and thus develops a better sense of operations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 8.
Joining and separating problems are perceived by students as active situations, easier to model and "see" as the start quantity increases or decreases. Part-part-whole problems, however, assume a static situation, as no action or change occurs, making them more abstract and difficult to understand. Comparing problems, on the other hand, deal with the relationship between two quantities by opposing them: thus, there is no action, but a comparison of one quantity to another.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83.
Joining Problems
The part-whole model can be useful for representing known and unknown values in joining problems. The set model is useful for representing the addition of a quantity.
- Joining : Result unknown. Jamil has 6 candies. He buys 5 more. How many pieces of candy does Jamil have now?
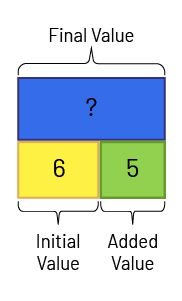
6 + 5 = ?
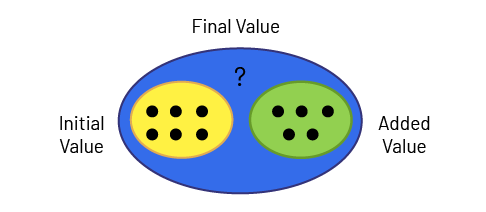
6 + 5 = ?
- Joining : Start unknown. Jamil has some candy. He buys 5 more. He now has 11. How many candies did Jamil have initially?
? + 5 = 11)
- Joining : Change unknown. Jamil has 6 candies. He buys a few more. He now has 11. How much candy did Jamil buy?
6 + ? = 11
Separating Problems
The part-whole model can be useful for representing known and unknown values in separating problems. The set model is useful for representing the subtraction of a quantity.
- Separating: Result unknown. Nadia has $15. She gives $5 to her brother. How many dollars does she have left now?
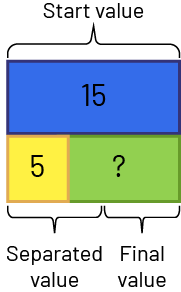
15 - 5 = ?
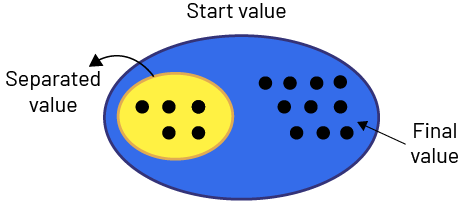
15 - 5 = 10
- Separating: Change unknown. Nadia has $15. She gives some dollars to her brother. She now has $10 left. How many dollars did Nadia give to her brother?
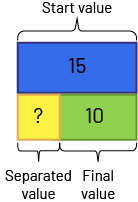
15 - ? = 10 15 - 10 = 5 therefore 15 - 5 = 10
- Separating: Start unknown. Nadia had a certain number of dollars. She gave $5 to her brother. She now has $10 left. How many dollars did Nadia have initially?
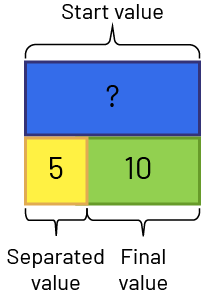
? - 5 = 10 10+ 5 = 15, therefore, 15 - 5 = 10
Part-Part-Whole Problems
The part-whole model can be useful for representing known and unknown parts or the known and unknown whole in part-part-whole problems.
- Part-part-whole: Part unknown. Sonia has 8 coloured pencils. Three of these crayons are red. The remaining crayons are blue. How many blue crayons does Sonia have?
\(\displaylines{\begin{align}8 \ - 3 &= \mathord{?} \\ 8 \ - 3 &= 5\end{align}}\)
- Part-Part-Whole: Whole unknown. Sonia has 3 red crayons and 5 blue crayons. How many crayons does Sonia have?
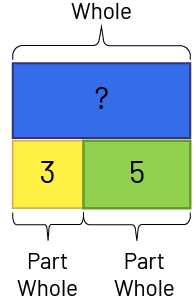
\(\displaylines{\begin{align}\mathord{?} \ - 3 &= 5 \\ 5 + 3 &= 8 \mathord{, \ donc\ }8 \ - 3 = 5\end{align}}\)
Comparing Problems
The linear model can be useful for representing the difference between two numbers in comparing problems. In this example, we use the Cuisenaire rods and the double number line.
- Comparing: Difference unknown. Judith has $6 and Jane has $3. How many more dollars does Judith have than Jane? OR Judith has $6 and Jane has $3. How much less does Jane have than Judith?
I know that the dark green rod represents 6, so I place it at the top of the number line starting at 0. I know that the lime green rod represents 3, so I place it below the number line at 0. I compare the two rods and see that the lime green ruler is 3 less than the dark green ruler. This is the difference or gap between the two quantities. There is a difference of $3. Jane has $3 less than Judith.
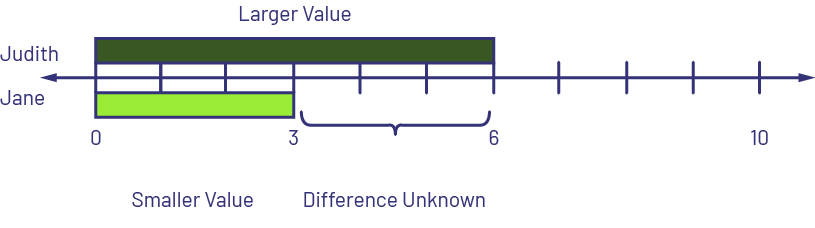
\(\displaylines{\begin{align}6 \ - 3 &= \mathord{?} \\ 6 \ - 3 &= 3\end{align}}\)
Comparing: Larger quantity unknown. Judith has $3 more than Jane. Jane has $3. How many dollars does Judith have? OR Jane has $3 less than Judith. Jane has $3. How many dollars does Judith have?
I know that the lime green rod represents 3, so I place it at the top of the number line starting at 0. I take another lime green rod and place it under the number line at 0 and add another lime green rod at the end of the first rod since Judith has $3 more than Jane. I replace the two lime green rods with the dark green rod that represents 6. Judith has $6.
- Comparing: Smaller quantity unknown. Judith has $6 and Jane has $3 less than Judith. How many dollars does Jane have? OR Jane has $3 less than Judith. Judith has $6. How many dollars does Jane have?
I know that the dark green rod represents 6, so I place it at the top of the number line starting at 0. On the number line, I count backwards three jumps to 3 to represent that Jane has $3 less than Judith. I take a lime green rod and place it under the number line starting at 0. This is how much Jane has. Jane has $3.
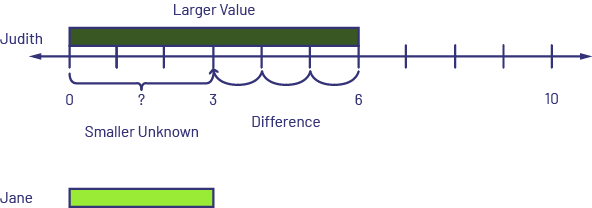
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 7-10.
Knowledge: Adding Problem
In adding problems (with whole numbers), the result is the largest number.
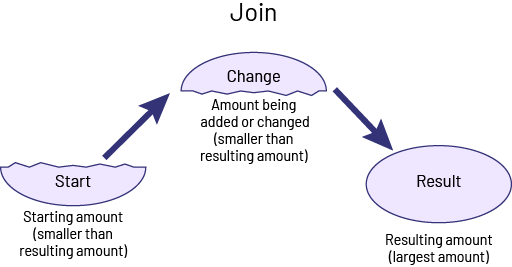
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Example:
Camille has 5 marbles. Luke gives her 8 marbles. How many marbles does she have in total?
Result unknown: 5 + 8 = ?
Camille has 5 marbles. She needs 13 marbles for her game. How many marbles does she need?
Change unknown: 5 + ? = 13
Camille has marbles. Luc gives her 5 more. Now she has 13. How many marbles did she have at the beginning?
Start unknown: ? + 5 = 13
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Knowledge: Take-away Problem
In take-away problems with whole numbers, the first amount is the largest.
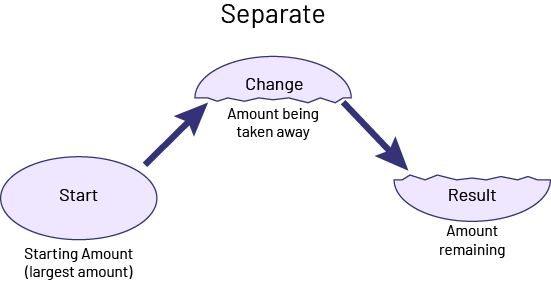
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Example:
Camille has 13 marbles. She gives 5 to her friend Luc. How many marbles does she have left?
Result unknown: 13 - 5 = ?
Camille has 13 marbles. She gives some to her friend Luc. Now she has 8 marbles left. How many marbles did she give to Luke?
Change unknown: 13 - 5 = 8
Camille has marbles. She gives 5 to her friend Luke. Now she has 8. How many marbles did she have initially?
Start unknown: ? - 5 = 8
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Knowledge: Part-Part-Whole Problem
Problems that focus on the part-part-whole relationship include two parts that are joined together as a whole.
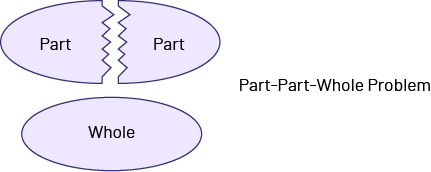
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9.
Example
Camille has 5 red marbles and 8 yellow marbles. How many marbles does she have?
Whole unknown : 5 + 8 = ?
Camille has 13 marbles: 5 are red and the others are yellow. How many yellow marbles does she have?
Part unknown : 5 + ? = 13
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Knowledge: Comparing Problem
In comparing problems, two quantities are compared. The third quantity is the difference.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10.
Example:
Camille has 13 marbles. Luke has 8 marbles. How many more marbles does Camille have than Luke?
Difference unknown: 13 - 8 = ?
Luke has 5 marbles. Camille has 8 more marbles than Luke. How many marbles does Camille have?
Larger quantity unknown: ? - 8 = 5
Camille has 13 marbles. She has 5 more than Luke. How many marbles does Luke have?
Smaller quantity unknown: 13 + ? = 5
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).