B2.5 Represent and solve equal-group problems where the total number of elements is no more than 10, including problems in which each group is a half, using tools and drawings.
Activity 1: Solving Grouping Problems
After a trip to the orchard, the teacher wants to give half an apple to each of the eight children. How many apples does she need?
STRATEGY
Using a Diagram to Represent the Problem
I draw 8 people. I divide an apple into 2 equal parts. I now have 2 halves. I place 1 half under the first person and 1 half under the second person. So I need 1 apple for 2 people. I draw 1 apple half under each of the other 6 people. So, I see that there are 8 halves shared between 8 people. So the teacher needs 4 apples for 8 children.
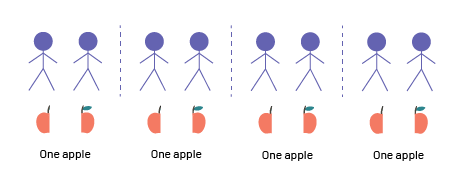
Source : adapted from En avant, les maths!, 1re, CM, Nombres, p. 3.
Activity 2: Solving Grouping Problems
Students are looking for their mittens in the basket. There are 10 mittens in the basket. How many students are there?
STRATEGY
Using a Rekenrek to Represent the Problem
I use a Rekenrek to represent this problem. I know that each student must have two mittens. I move 2 beads to the left on the first rod. I move 2 more beads to the left on the next rod. I now have 4 beads. Counting in intervals of 2, I continue to move 2 beads per rod until I have reached 10, or 2-4-6-8-10 mittens. I count the number of rows of 2 beads, and there are 5. So I know there are 5 students looking for their mittens in the basket.
Source : adapted from En avant, les maths!, 1re, CM, Nombres, p. 4.