B1.3 Estimate the number of objects in collections of up to 200 and verify their estimates by counting.
Skill: Estimating the Number of Objects
An understanding of the concept of quantity is essential for developing the ability to estimate, judge magnitude, and appreciate proportional relationships. Students develop their estimating skills by becoming aware of relationships between quantities (for example, Is this quantity closer to 10 or 20?) and by judging magnitude. For example, a student who estimates that there are 100 tokens in a set when there are really only 40 tokens has not developed a good sense of magnitude. However, someone who estimates that there are 50 tokens in a set has a better sense of magnitude. Therefore, students should be trained in the early grades to question the reasonableness of their estimations. Manipulatives (for example, ten frames) help them develop the skill of estimating, as it allows them to visualize quantities.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 45.
Estimation is a process by which visual and mental information is used to assess the magnitude of a quantity. Estimations are an important part of our daily communication because they give us approximate quantities. Estimations are used by the media (for example, nearly 200 people were at the rally) or by us in our interactions (for example, grocery shopping costs about $200 per week).
As with the teaching of mathematical concepts in general, estimation should be used in a problem-solving context. In order to develop students' understanding of the concept of estimating a quantity, it is even better to present them with problems in which only the estimation is being sought (for example, About how many pages of the dictionary do I have to read to get through the definitions of 100 words?) Sometimes it may be valuable to compare estimations to the exact quantity to examine the effectiveness of estimation strategies and the accuracy of estimations. However, this should not be done routinely, or students will not see the relevance of the estimations, since the answer sought seems to have to be the exact quantity.
Students often believe that an estimation is a guess or that only one estimation can be considered acceptable, when what matters in the estimation is the magnitude, not the number. A good estimation is a number that roughly defines the quantity being estimated. Certainly, however, efficiency in estimating demonstrates a good sense of number. There are no set rules for how to do this and no set goal: the context of each problem and the size of the numbers will determine the acceptable degree of accuracy. An estimation, for example, of about 60 blocks or about 40 blocks is very acceptable when the actual quantity of blocks is 50, whereas an estimation of about 200 would be the result of guesswork or an inefficient strategy. On the other hand, if the actual quantity is 175 blocks, estimations of about 150 or 200 become acceptable, since the difference between the estimation and the exact quantity is negligible given the size of the actual quantity.
In estimation situations, in order to clarify that the number represents an approximate quantity, it is important that students communicate the estimate using "approximation" language, such as about, at least, near, a little more than, about, more or less , or between; for example, about 100 people were at the party, it is about 1 m tall, it is a little less than 5 kg, it is a little more than $200, it will take between 4 and 5 hours to drive. These instructional strategies help to dispel the impression that there is a single "right" estimation and to recognize the value of different estimations and their degree of accuracy.
In order to estimate, a comparison must be made between the quantity to be estimated and some benchmark; for example, Rachelle and Oman are wondering how many students are playing in a specific part of the schoolyard. As they think about it, they can use a benchmark such as the number of students in their class group, which is 20 students. This known real-life situation helps them to mentally picture a certain number of people in a given space and to estimate whether there are fewer than 20 people on the field or, on the contrary, whether there are between 20 and 40 students (twice as many) or nearly 60 people (three times as many). It is important to know that when estimating with benchmarks, students apply proportional reasoning between a known amount (20 students in a certain space) and an unknown amount (the number of students in another space).
Sometimes students do not have integrated benchmarks for a given situation and therefore need to use another strategy. They can count a subset of objects and use that number as a benchmark to estimate the total number of objects. For example, if asked to estimate the number of marbles in a jar, students might first take a handful of marbles and count them so that they can compare this benchmark quantity to the contents of the jar. They could also count the marbles in the bottom of the jar (10 black marbles) and then estimate the number of rows of marbles in the jar (about 9 rows) to be able to estimate the total number of marbles in the jar (90 marbles). Students can also separate the quantity into sections and estimate the quantity in each section.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36-38.
Skill: Counting (Checking Estimations Using Counting Strategies)
Counting involves both reciting a series of numbers and associating them with a series of objects.
By the time they enter kindergarten, children have usually learned to count and may be able to count up to large numbers, usually using their memory and reciting the numbers continuously, as they do with the letters of the alphabet. However, if they are asked what the number is after 5, they may start counting back to 1 without really understanding the question. Young children may not understand that we always count in the same way. For example, some children count by saying "1, 2, 3, 4, 5, 6, … " one time and "1, 2, 3, 5, 4, 6, 8,…" another time, without noticing the inconsistency. If asked to count objects, they may not associate each object with a number in the count, or they may touch two items while saying one number (for example, fourteen), so the count may not produce the same result each time. Children also sometimes do not understand that any set of objects (even very different objects, such as cookies and apples) can be counted at the same time and that one can start counting from any object in the set and arrive at the same number.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 10.
Counting involves being able to relate a quantity to the name or symbol of the number that represents it.
Part of the complexity of the counting activity is that it requires a connection between the name
or symbol of a number and the quantity it represents, a connection that children do not immediately grasp (for
example, the word "five" and the symbol "5" represent not only the 5e object counted
and the 5e digit in the set of numbers they have learned to recite, they also represent the quantity of
objects counted). It is essential that children make this connection between the quantity value of a number and its
role in the counting sequence. If they are asked what the quantity of objects is at the end of a count, some children
may begin counting again without understanding that the last number said is actually the quantity of objects in the
set.
Learning to count to large numbers is a valuable experience. However, children must first develop an understanding of the concept of quantity and the relationships between numbers by working with small numbers. They may be able to count very far but still have limited knowledge of the quantity represented by the result of a count; for example, they may be able to count to 30 but be unable to show 30 objects in a larger set of objects. Therefore, students should be given multiple opportunities to make the connection between the name or symbol of a number and the quantity it represents.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 11.
The purpose of this section is to help teachers understand some of the basic concepts involved in the early
development of counting skills. The acquisition and mastery of these concepts does not necessarily occur in a
predetermined order. Students, for example, may learn parts of one concept, move on to another, and then return to the
previous one.
The following list of concepts is not intended to present a pathway for students to follow faithfully. Rather, it is a tool to help teachers understand the elements involved in the skill of counting. It is not necessary for students in the early grades to know the names of these concepts.
Stable order : – The idea that the counting sequence stays consistent; for example, we always say "1, 2, 3, 4, 5, 6, 7, 8" and not "1, 2, 3, 5, 6, 8".
Order irrelevance: The idea that the counting of objects can begin with any object in a set and the total will still be the same.
Abstraction: A quantity can be represented by different things; for example, 5 can be represented by five identical objects, by five different objects, by five invisible things, such as ideas, or by five points on a line. Abstraction is a complex concept, but most students grasp it fairly easily.
Conservation: Counting a set of objects remains the same whether the objects are scattered or moved closer together.
One-to-one correspondence: The idea that each object being counted must be given one count and only one count. In the early stages, it is useful for students to tag each item as they count it and to move the item out of the way as it is counted.
Cardinality: The idea that the last count of a group of objects represents the total number of objects in the group. A child who recounts when asked how many candies are in the set that he or she has just counted does not understand cardinality.
Movement is magnitude: As one moves forward in a sequence of numbers, the quantity increases by a constant interval of 1 and as one moves backward in the sequence, the quantity decreases by 1. By extension, counting intervals other than 1 are included under this element; for example, if one counts in intervals of 5, the quantity increases by 5 throughout the sequence and if one counts backward in intervals of 2, the quantity decreases by 2 throughout the sequence. Students can use this element to facilitate learning basic number facts; for example, knowing that , they can learn that , since it is 1 more.
Unitizing or grouping according to base 10: The idea that, in the base ten system, objects are grouped into tens once the count exceeds 9 (and into tens of tens when it exceeds 99) and that this grouping of objects is indicated by a 1 in the tens place of a number once the count exceeds 9 (and by a 1 in the hundreds place once the count exceeds 99).
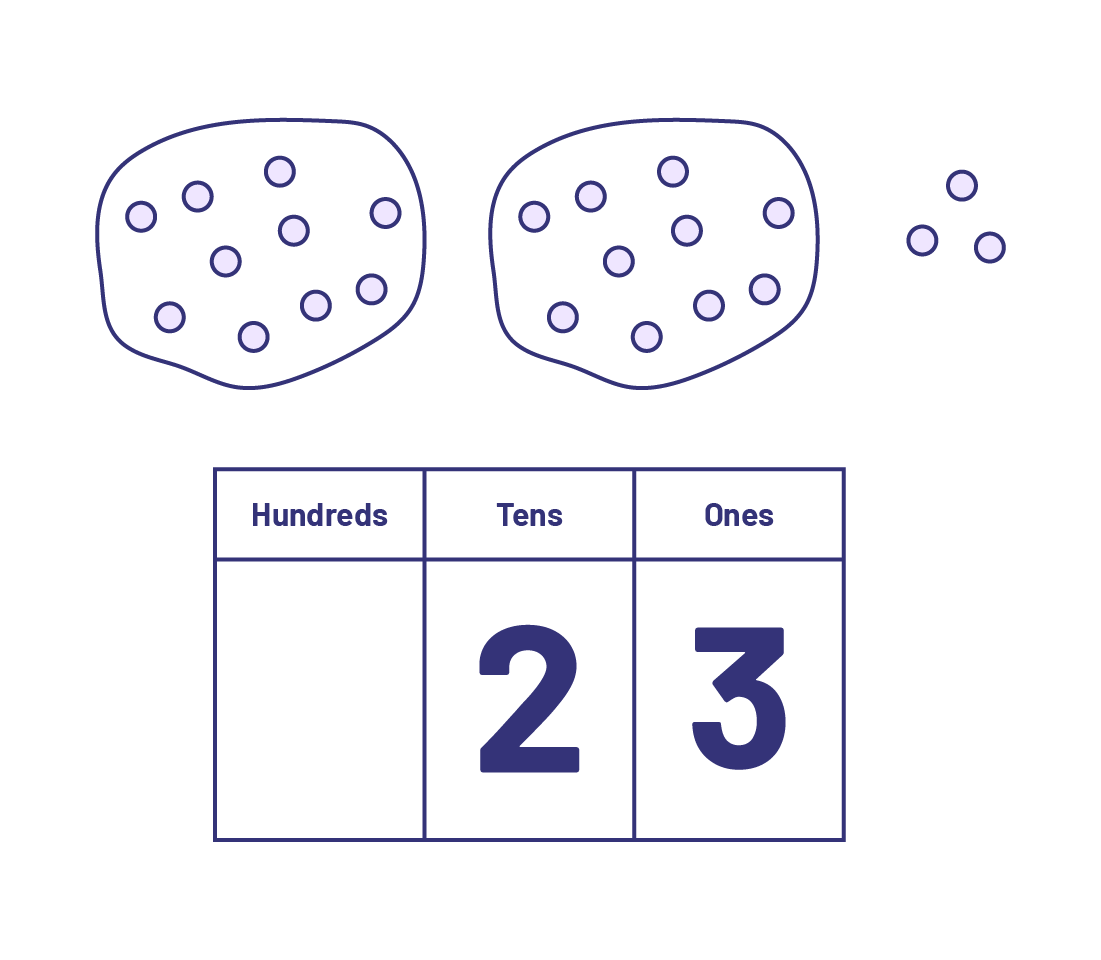
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 13-14.