B1.7 Recognize that one third and two sixths of the same whole are equal, in fair-sharing contexts.
Skill: Recognizing Equivalence
To recognize the equality of two fractions is to recognize that both fractions represent the same quantity.
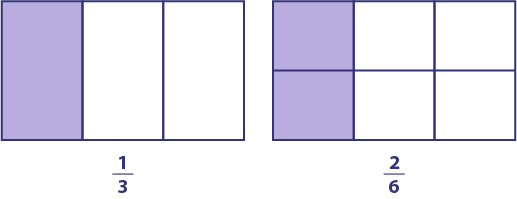
It is sometimes difficult for students to grasp that a quantity can have several names and be represented by several numbers (for example, \(\frac{1}{3}\) represents the same quantity as \( \frac{2}{6}\); therefore, we can say that \(\frac{1}{3}\ = \frac{2}{6}\)).
Understanding equivalent fractions is part of the proportional reasoning that students will continue to develop over the next several grades.
Determining equivalent fractions means determining fractions that represent the same quantity, or part of the whole. We are looking for a number of "equal small parts" that correspond to the number of "equal large parts" that corresponds to the same area of the whole. If, for example, we are looking for the number of sixths that correspond to one third, we can represent the two fractions using identical area models in order to find the equivalence.
Equivalence relation can also be explored with fractions of a set. In the image below, students can easily see that \(\frac{2}{6}\) of the candies are wrapped in red foil wrappers. However, they may have difficulty determining the equivalent fraction, \(\frac{1}{3}\). It is therefore important to present students with activities that allow them to manipulate the elements of the whole, so they can group them into sets of 2 to determine the equivalent fraction.

\(\frac{2}{6}\) sweets are wrapped in red wrappers.
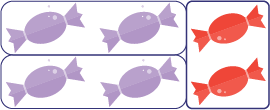
\(\frac{1}{3}\) sweets are wrapped in red wrappers.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 50-52.
Knowledge: Equivalent Fractions
Two fractions are equivalent if they represent the same quantity.
Note: In grade 2 , it is important to emphasize that these are fractions of the same whole. The same part of a whole can be represented by different fractions (for example, one third and two sixths are equivalent fractions).
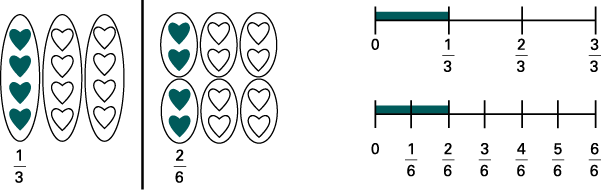
Source: translated from En avant, les maths! 2e, CM, Nombres, p. 2.
