B2.1 Use the properties of addition and subtraction, and the relationships between addition and multiplication and between subtraction and division, to solve problems and check calculations.
Skill: Use the Properties of Addition and Subtraction to Solve Problems and Check Ccalculations
Using the properties of operations and the relationships between operations allows us to construct number sentences and manipulate them flexibly in order to solve equations and simplify calculations.
(Department of Education and Training of Western Australia, First Steps in Mathematics: Number - Understand Operations, Calculate, Reason About Number Patterns, vol. 2, 2005, p. 66)
In the primary grades, students make connections between operations through various activities. For example, they know the identity rule, that addition and subtraction are inverse operations and that addition is commutative. Over time, students develop their number sense and operations sense and gradually use them before performing operations. This practice, while often informal and mental, is still essential to understanding the relationships between numbers and between operations.
Source : Guide
d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97.
It is not necessary for primary students to know the names of the properties. They just need to use them naturally to
combine numbers.
Students demonstrate their understanding of the properties of mathematical operations through specific objects or numbers and use manipulatives, drawings, words, or symbols to represent mathematical ideas and relationships.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 17.
The properties of addition are:
- commutative property (for example, 1 + 2 = 2 + 1);
- associative property (for example, (8 + 9) + 2 = 8 + (9 + 2));
- identity property (for example, 1 + 0 = 1).
The property of subtraction is :
- the identity property (for example, 1 - 0 = 1).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 33.
Commutative Property
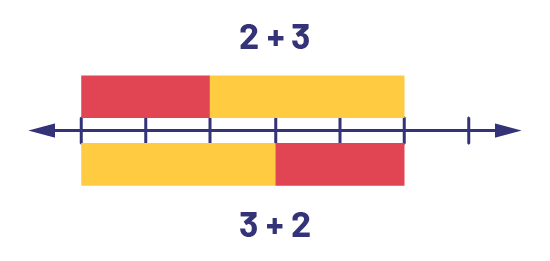
Students who recognize the commutative property of addition can cut the amount of math facts they need to learn in half. Visual representation of facts such as (3 + 2) and (2 + 3) helps students grasp this relationship.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 19.
Associative Property
The associative property allows the terms of an expression to be combined in different ways without changing the value; for example, in the expression 15 + 13 + 17, it is possible to combine 13 and 17 to get 15 + (13 + 17), which gives 15 + 30, or 45. It is also possible to combine 15 and 13 to get (15 + 13) + 17, which gives 28 + 17, or 45.
The associative property does not change the order of numbers in a numerical expression. However, associativity and
commutativity can be combined to facilitate the evaluation of a numerical expression. To determine the value of the
expression 19 + 27 + 11, we can determine the value of (19 + 11) + 27, because the 9 and the 1 are complementary
and give a ten, so we can get the answer mentally, 30 + 27. By exposing students to a wide range of activities, the
teacher can help them understand and use the different properties effectively.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 105-107.
Important!
Parentheses are used to ensure mathematical accuracy of the message. However, with 2nd graders, it is best to stick to less abstract ways of highlighting combinations; for example:
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 2e année, p. 98.
Identity Property
Using the identity property, encourage students to propose conjectures such as, "If I add zero to a quantity
(for example, \(5 + 0\)), that quantity stays the same and if I add any quantity to 0 (for example, \(0 + 5\)), I get
the added quantity."
By applying these conjectures to different numbers, students will be able to formulate a generalization that this
property is true for all numbers.
For the identity property in subtraction, encourage students to propose a conjecture such as, "When I subtract 0 from a number (for example, \(5 - 0\)), I get the starting number." By applying this conjecture to different numbers, students will be able to make a generalization that this property is true for all numbers.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 93 and 95.
Skill: Using the Relationship Between Addition and Subtraction to Solve Problems and Check Calculations
Addition and Subtraction
Understanding the connections between operations (for example, addition and subtraction are inverse operations) helps students learn basic number facts and solve problems.
Source: Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.
Addition and subtraction are inverse operations. Students who are learning often have difficulty solving equations such as (17 + ? = 31). Many teachers encourage them to use the inverse operation, subtraction. However, this can be a learning trick unless students understand why subtraction is a possible strategy. To do this, they must first grasp the relationship of the whole to its parts and the meaning of a difference; for example, a number can be represented as :
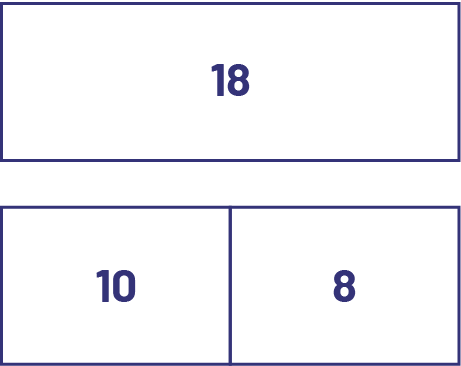
This way of representing the relationship between a number and its parts allows us to see that subtraction is the
inverse operation of addition. Thus, since 10 + 8 = 18 and 8 + 10 = 18, then 18 - 10 = 8 and 18 - 8 = 10. In addition,
students can understand why addition is commutative 10 + 8 = 8 + 10 and subtraction is not (\(18 - 10 ≠ 10 -
8\)). Students who have developed good number sense and are able to decompose and combine numbers can use their
knowledge to more effectively solve equations such as \(10 + \mathord{?} = 18\) by understanding that we are looking
for the difference between 10 and 18.
Source : adapté du Guide d'enseignement efficace des mathématiques de la 4e à la 4e année, p. 97-98.
Multiplication and Addition
The connection between multiplication and addition is often the starting point for introducing students to the concept of multiplication. Early in learning multiplication, students recognize that the situation presents the same quantity "many times" and use equal groups to represent the situation and repeated addition to get the answer.
Source : Guide d'enseignement efficace des mathématiques de la 2e à la 4e année, p. 85.
Since multiplication can be seen as repeated addition (for example, 3 times 5 = 5 + 5 + 5), students can relate the doubles strategy (for example, 4 + 4 = 8) to multiplication by two. The connections between addition and multiplication can also help them learn some basic math facts; for example, a student who knows that 3 times 4 = 12 will be able to learn that 4 times 4 = 16, since 4 times 4 = 16 is equivalent to 3 times 4 + 4 = 16.
Source: Guide d’enseignement
efficace des mathématiques de la 1re à la 3e année, p. 32.
By solving a variety of problems and discussing strategies, students come to make and understand the connection between the word "times" and the sign "times", a crucial step in developing an understanding of multiplication. Once their sense of multiplication is well established, they will use the multiplication operation more regularly to obtain answers.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 86.
Division and Subtraction
Similarly, division can be associated with repeated subtraction, but not in the same way. The product of a multiplication is equal to the sum resulting from the repeated addition, while the quotient of a division is equal to the number of repeated subtractions (for example, to calculate \(20\; \div \;5 \), we do \(20\; - \;5\; = \;15,\;15\; - \;5\; = \;10,\;10\; - \;5\; = \; 5,\;5\; - \;5\; = \;0\); we subtracted 4 times; therefore \(20\; \div \;5\; = \;4\)).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 98-99.
Division can be seen as repeated subtraction or addition (for example, \(24 - 4 - 4 - 4 - 4 - 4 - 4 = 0\), so it takes 6 groups of 4 to make 0 or \(4 + 4 + 4 + 4 + 4 + 4 = 24\), so it takes 6 groups of 4 to make 24) or as dividing into equal parts.
Source: Guide d'enseignement
efficace des mathématiques de la 1re à la 3e année, p. 32.
It takes time for students to learn these relationships. To achieve this, teachers can use hands-on activities, problem solving, and mathematical exchanges that focus on the connections between operations.
Knowledge: Commutative Property
An operation is commutative if its result remains unchanged when the order of its terms is reversed. For example, addition is commutative. However, subtraction is not a commutative operation.
Example
\(2 + 3 = 3 + 2\)
\(6 - 3 ≠ 3 - 6\)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, 102.
Knowledge: Associative Property
The associative property is a property of addition and multiplication. It allows the terms of an expression to be combined in different ways without changing their value.
Knowledge: The Identity Property
The identity property occurs when a number is combined with a special number (identity element) by using one of the operations, and the result leaves the original number unchanged. In addition, and subtraction, the identity element is 0; for example, for example, \(7 + 0 = 7\) and \(0 + 7 = 7\).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 105-107.
Knowledge: Relationships Between Addition, Subtraction, Multiplication and Division
Addition and subtraction are inverse operations.
Multiplication can be associated with repeated addition.
Division can be associated with repeated subtraction.