At a Glance...

Activity 1: I Am Making a Necklace! (Commutative Property of Addition)

---

Ask students to make a necklace by stringing 5 red beads and 2 blue beads, then suggest they write the corresponding number sentence.

Have students turn the necklace and write the corresponding number sentence.

Then suggest that students compare the two number sentences and answer the following questions:

• What do you notice about the order of the beads?
• What do you notice about the amount of beads?
• Why is the quantity the same in both cases?
• Change the amount of beads on the necklace and write two number sentences. Compare the sentences. What do you notice?

Notes: 

• Repeat the activity, increasing the amounts of blue and red beads. 
• Repeat the activity, asking students to move to look at the necklace in the other direction instead of turning it.

Activity 2: How Many Toys?

---

Present students with six toys and ask them to count them.

Cover the toys with a cloth and tell them that you will add a mystery number of toys.

Pretend to add toys, but do not add anything. Remove the cloth and ask the following questions:

• How many toys are there now?
• How many toys did I add?

Ask students to write a number sentence to represent the situation.

\(6 + 0\)

Repeat the activity, adding 6 toys to 0 toys to represent (0 + 6).

Point out that since 6 + 0 = 6 and 0 + 6 = 6, we can conclude that 6 + 0 = 0 + 6. Explain to students that a special fact about addition is that it doesn't matter in which order we add the numbers. 

Encourage students to propose a conjecture about what happens when we add zero to a number, then ask questions such as:

• Could you apply your conjecture to other numbers? Give it a try.
• Could you apply your conjecture to all numbers? Why or why not?

Extension

Present students with 8 toys and ask them to count them. Cover the toys with a cloth and tell the students that you will remove a mystery number of toys.

Pretend to remove toys, but do not remove anything. Remove the cloth and ask students the following questions:

• How many toys are there now?
• How many toys did I remove?

Ask students to write a number sentence to represent the situation.

\(8 - 0 = 8\)

Encourage students to propose a conjecture about what happens when we subtract zero from a number, and then ask them questions such as:

• Could you apply your conjecture to other numbers? Give it a try.
• Could you apply your conjecture to all numbers? Why or why not?

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 94 and 95.

Activity 3: Train Cars

---

Introduce students to three train cars constructed with interlocking cubes of different colours.

Ask the students to help Mr. Bontrain, the conductor, who wants to combine two cars without changing their order. How can he combine the cars?

Represent each possible combination using the interlocking cubes and write the corresponding number sentence. To avoid using parentheses, use boxes to illustrate the cars.

Note: Cars can be combined in two ways:

• combine cars 1 and 2;

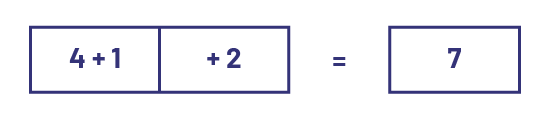
• combine cars 2 and 3;

Ask students the following questions:

• Are there other possible car combinations? How do you know?
• What is the sum of the interlocking cubes that form the train in each case? (Both sums are equal to 7; they are the same)

• How is it possible that the sum remains the same even though there are different combinations of cars? (These are the same interlocking cubes combined differently; the total amount of cubes does not change)
• Would this work with three other numbers? Demonstrate this with a double open number line and a number sentence.

Ask students to explain their observations to another student. Afterwards, ask them the following question:

• What could you write in your collective math journal about what you discovered today?

Repeat the activity using a larger number of cars.

Note: If students are familiar with the commutative property, some may change the order of the terms to be added (for example, (4 + 2 + 1)). If so, ask them to justify why the order can be changed. Otherwise, simply mention that the order of the cars cannot be changed, since they are attached to the engine in this way.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 3^e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 99-100.