B2. Operations
Use knowledge of numbers and operations to solve mathematical problems encountered in everyday life.
Learning Situation 1: Groups of 2, 3, 4 or 5
Total duration: approximately 2 hrs 30 min
| Overall Expectation | Specific Expectations |
|---|---|
| B2. Operations Use knowledge of numbers and operations to solve mathematical problems encountered in everyday life. |
B2.6 Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays. B2.7 Represent and solve problems involving multiplication and division, including problems that involve groups of one half, one fourth, and one third, using tools and drawings. |
Learning Goals
The purpose of this learning situation is to allow the student to:
- represent multiplication using concrete materials, an array or a number line;
- make connections between concrete, graphic, verbal and symbolic representations of multiplication.
Equal Groups

4 groups of 3
The Array

4 rows of 3
Number Line

4 jumps of 3
Prerequisites
In this learning situation, students should be able to:
- represent addition using concrete and semi-concrete materials;
- communicate addition using number sentences;
- use addition facts up to 18 (9 + 9).
Mathematical Vocabulary
multiplication, equal groups, product, factor
Materials
- large sheets of paper
- counters
- sheets of paper
Before Learning (Warm-Up)
Duration: approximately 50 minutes
Find everyday examples of combinations of 2, 3, 4 or 5 to stimulate thinking about things found in groups..
Group students in pairs and ask them to make their own list of things found in groups of 2, 3, 4 or 5.
Gather students and write their ideas on a chart on large sheets of paper or on the interactive whiteboard.
| 2 | 3 | 4 | 5 |
|---|---|---|---|
|
The wheels of a bicycle Eyes The horns of a bull Socks and shoes Twins |
The wheels of a tricycle The legs of a tripod The sides of a triangle The leaves of a clover Triplets |
The tires of a car The legs of a chair The sides of a square The legs of an animal |
School days Fingers Toes |
Ask the following questions:
- Is it easier to find examples of things that are in groups of 2, 3, 4 or 5?
- For which number was it most difficult to find examples?
Then ask students to name things found in groups of 6 (for example, insect legs), 7 (for example, days of the week), and 8 (for example, tentacles of an octopus). Write the examples provided in new columns of the chart.
Propose a problem-solving situation using an example from the table above. For example: "A spider has 8 legs. How many legs are there if there are 3 spiders?
Give students counters and ask them to solve the problem and record their approach.
Invite a few students to share their solution and explain their approach.
Build on students' ideas about creating equal groups of 8 counters to explain that multiplication is repeated addition.
Ask the following questions:
- How many groups did you form? How many counters were in each grouping?
- How do the groups of counters illustrate the problem?
- How could you use addition to determine the total number of legs? (8 + 8 + 8)
- How can we represent 3 groups of 8 by multiplication?
- What is the product of 3 times 8?
- What are the different ways to determine the product of 3 and 8?
Use counters, drawings, arrays, words, and number sentences to solve other problems with students (for example, "A tricycle has 3 wheels. How many wheels are there if there are 4 tricycles?").


Active Learning (Exploration)
Duration: approximately 50 minutes
Place counters and sheets of paper out for the students to use.
Group students in pairs and ask them to compose other problems based on the ideas on the board.
Have students represent their multiplication problems in a variety of ways on a large sheet of paper.
Example

Consolidation of Learning
Duration: approximately 45 minutes
Ask each team to present their work and explain it to the rest of the class.
Ask the following questions:
- What do you notice about the different representations?
- How can you explain to someone what 5 times 2 means?
- What drawing can be made to represent 3 times 6?
- Can you compose a problem that has 3 times 6 as a number sentence?
Pose similar problems to deepen students' understanding:
- If a carpenter has 15 legs to use for stools, how many 3-legged stools can they make?
- If there are 14 wheels attached to the bike rack, how many bikes are there?
- If there are 16 hands on a bench, how many people are there?
- If there are 24 legs in a field, how many horses are there?
Invite students to explain their approach to solving each problem.
Have students write in their math journals what they learned about multiplication.
Examples of Success Criteria
The student:
- makes equal groupings to represent the concept of multiplication;
- explains the meaning of multiplication using any mode of representation (manipulatives, drawings, arrays, words or number sentences);
- explains the relationships between the different modes of representation.
Differentiated Instruction
The activity can be modified to meet the needs of the students.
| To Facilitate the Task | To Enrich the Task |
|---|---|
| Initially, use numbers that work well for skip counting by 2s, 3s, and 5s. |
|
Extension
The Broken Calculator
Materials
- calculator (1 per student)
Have students use a calculator to determine the product of number sentences.
Explain that all the keys can be used except the multiplication key, because it "doesn't work".
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 185-191.
Learning Situation 2: What is the Relationship?
Total duration: approximately 2 hrs 30 min
| Overall Expectation | Specific Expectations |
|---|---|
| B2. Operations Use knowledge of numbers and operations to solve mathematical problems encountered in everyday life. |
B2.1 Use the properties of operations, and the relationships between multiplication and division, to solve problems and check calculations. B2.6 Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays. |
Learning Goals
The purpose of this learning situation is to allow the student to:
- explore the relationships and patterns that exist between numbers and various operations.
| Learning Context | Prerequisites |
|---|---|
|
Arrays are very useful tools for developing a sense of multiplication and division operations and an understanding of their properties. Various examples of arrays can be found (for example, calendar, checkers board, floor tiles) and used in learning situations. Students first construct arrays using concrete materials (for example, counters, cubes, tiles) to represent multiplication or division. Then they also build them using grids. Examples 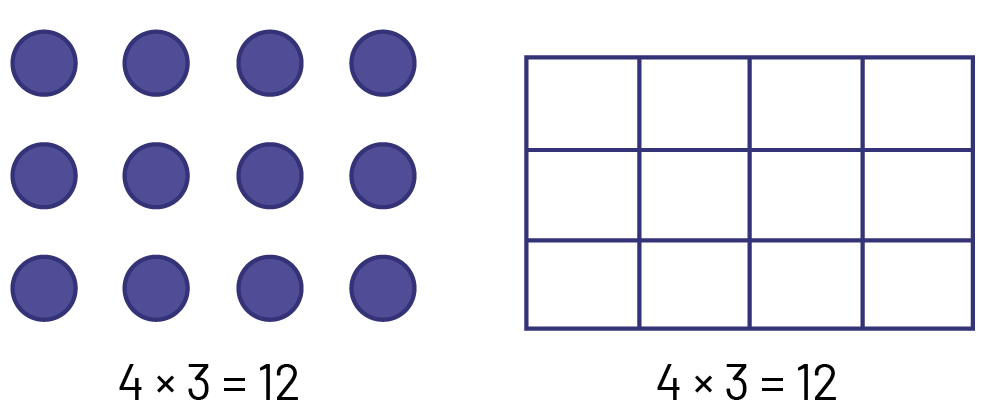
In the junior grades, students are able to use a more abstract model of arrays (for example, open array) as a multiplication and division strategy. Example 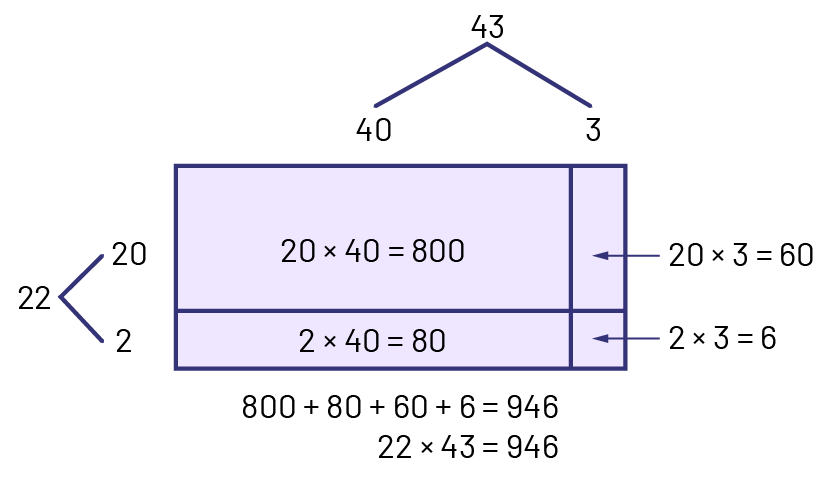
Arrays can be used to represent:
|
In this learning situation, students will:
|
Mathematical Vocabulary
grid, array, row, column, equal parts, multiply, divide, add, subtract, partitioning, distribute
Materials
Main Activity
- Appendix 3Rel.1 (1 set of number cards per team of 2)
- Appendices 3Rel.2 (a) and 3Rel.2 (b) (Array Booklet) (1 copy per student)
- large sheets of paper
- construction paper
- reusable plastic bags (1 per team of 2)
- counters or other identical objects (30 per team of 2)
- straws, pencils or pieces of string
- bingo markers, stickers or ink pads
- 2 cm grid paper
Before Learning (Warm-Up)
Duration approximately 50 minutes
Prepare a grid of \(3 \times 4\) squares on a large sheet of paper and stick pieces of construction paper of the same colour and same dimensions on the squares.
Place it on the floor and have the students sit around it so that everyone can see it.
Ask the following questions:
- What do you see on this sheet? (for example, pieces of construction paper on grid squares)
- How are the pieces arranged (for example, in rows and columns)
- Why do you think the pieces of construction paper are arranged in rows and columns? (for example, it's a clear, orderly organization that gives a good overview, avoids wasting space, allows you to quickly see how many items there are)
- How many columns are there?
- How many pieces of construction paper are there per column?
- How many rows are there?
- How many pieces of construction paper are there per row?
- How many pieces are there in total?
- What number sentence could you use to describe this representation?
- Do you know of places where objects are arranged in rows and columns as if they were placed on a grid (for example, cereal and food boxes in a grocery store, chairs in a gym, tiles in a deck, cars in a parking lot, eggs in an egg carton, trees in a plantation, corn plants in a field).
Note: This activity could be modified for the interactive board.
Active Learning (Exploration)
Duration: approximately 60 minutes
Discuss possible number sentences from arrays found in everyday life.
Project 16 counters arranged in 2 rows of 8 counters or place 16 objects on the floor in 2 rows of 8 objects.

Ask students to describe the different ways in which the 16 counters or objects can be arranged in equal columns or rows (for example, students may observe that there are 16 counters or objects arranged in 8 columns of 2 counters or objects or in 2 rows of 8 counters or objects);

Ask students to determine the number sentence that corresponds to the various groupings of counters.
Examples
\(4 + 4 + 4 + 4 = 16\)
\(4 \times 4 = 16\)
\(16 - 4 - 4 - 4 - 4 = 0\)
\(16 \div 4 = 4\)
Write the number sentences proposed by the students on the board.
Form teams of 2 and give each team a bag containing 30 counters and a deck of cards prepared using Appendix 3Rel.1.
Ask students to:
- draw a card from the bag;
- represent, with the help of counters, the number in an array;
- place pencils, straws, or pieces of string on the array to represent equal groups of counters;
- represent other possible groupings.
Distribute a copy of Appendices 3Rel.2 (a) and 3Rel.2 (b) to each student and ask them:
- reproduce the arrays in their math journals using bingo markers, stickers or ink pads;
- write down all the number sentences corresponding to each of the arrays.
Consolidation of Learning
Duration: approximately 40 minutes
Invite each team to present a different array and explain what they did.
Ask the following questions to stimulate discussion and reflection:
- How many different arrays have we created?
- Who created an array to represent the number 18? Who created a different array for this number?
- What arrays can be created to represent the number 12?
- Explain the relationship between addition and subtraction, addition and multiplication.
- Explain the relationship between multiplication and division.
Examples of Success Criteria
The student:
- creates various arrays to represent a number;
- formulates the number sentences corresponding to the various arrays;
- explains the relationship between multiplication and addition;
- explains the relationship between multiplication and division;
- uses a number sentence corresponding to multiplication to discover a number sentence describing division.
Differentiated Instruction
The activity can be modified to meet the needs of the students.
| To Facilitate the Task | To Enrich the Task |
|---|---|
|
Have the student cut out different rectangles representing a number using 2 cm grid paper rather than counters, cut them out and glue them in their math journal under the chosen number. |
Follow-up at Home
Recycled Items
At home, the student can represent a number using recyclable items such as bread bag clips, pop can tabs, small rocks, etc. arranged in equal rows and columns and describe the arrays they made.
Source: translated from Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 201-206.
