B1.1 Read, represent, compose, and decompose whole numbers up to and including 1000, using a variety of tools and strategies, and describe various ways they are used in everyday life.
Skill: Reading Whole Numbers
Reading numbers allows them to be interpreted as quantities when expressed in words or numbers, or represented with concrete materials or models.
A quantity describes an order of magnitude (the "how much" or the "how much more") and is an essential concept in the development of number sense.
When toddlers recite numbers, they do not immediately make connections between the numbers recited and the notion of quantity. Then, when students learn to count, they mechanically associate each number 1, 2, 3, 4, 5 with one of the objects in a given set of objects without necessarily grasping that 5, the result of the counting, also corresponds to the quantity of objects in the set. The link between the quantity and the number that represents it is very complex. The same number, for example 2, can describe very different realities. It can represent 2 apples, 2 loaves of bread, or 1 apple and 1 loaf of bread at the same time. It can represent 2 big balloons as well as 2 small balloons. Thus, even if the sets of objects are different, the quantity of objects in each set is the same. The complexity is increased when the quantity refers to a measurement (for example, length, mass, capacity), since the "quantified objects," the units of measurement (for example, cm, kg, mL), are not manipulatable in the same way that, for example, apples, loaves of bread, or balloons are.
It is important to understand the concept of quantity to understand the concept of place value.
The concept of quantity is involved in understanding the concept of the place value of the digits that make up a number. This value increases successively by a factor of 10 when the digits are read from right to left and decreases by a factor of 10 when they are read from left to right. Understanding the concept of place value is also very helpful when students begin to use larger numbers or decimal numbers.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 44-45.
Developing a conceptual understanding of counting has a direct link to understanding quantity and place value
By counting concrete materials, students develop the basic concepts and strategies that help them understand the quantitative value of number. Students learn to count accurately, to recognize patterns in the base-10 numbering system (for example, 11, 12, 13…; 21, 22, 23…; 31, 32, 33…), and to make connections between these patterns and the place value of the digits that make up the numbers. Teachers must take into account that some numbers are particularly difficult to learn in English. For example, consider a number like 11, which some students will spontaneously call "one-teen", or the numbers 20 and 30, which students might see as "twoty or threety".
Example 1
Help students learn the numbers 11-16 and recognize that they do not follow the regularity of numbers 20-69 (for example, twenty-one, thirty-one, forty-one). Point out, for example, that the numbers 11-16 are formed from the numbers 1-6 and that some begin with the same letters (two and twelve; three and thirteen; four and fourteen; six and sixteen).
Example 2
Help students identify patterns in a number chart such as:
- The number 9 always ends the decade (for example, 29, 39, 49).
- In the sequence 10, 20, 30, …, the tens digit follows the same sequence as 1, 2, 3,…
- The sequence of numbers within each decade is formed from 1, 2, 3, … (for example, 20 combines with 1 to become 21, then with 2 to become 22, and so on).
- Even numbers always end in 0, 2, 4, 6 or 8.
- Odd numbers always end in 1, 3, 5, 7 or 9.
Key Concepts
According to the most recent educational literature, the following are considered to be basic concepts for the development of understanding quantity.
Conservation Principle
The counting of a set of objects remains the same whether these objects are scattered or close together.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 12-13.
Subitizing
The ability to subitize is the ability to quantify the elements of a given set of objects without counting each element. Activities designed to develop this skill (for example, using dot cards) help students develop a mental representation of the quantity associated with a number.
Dot cards
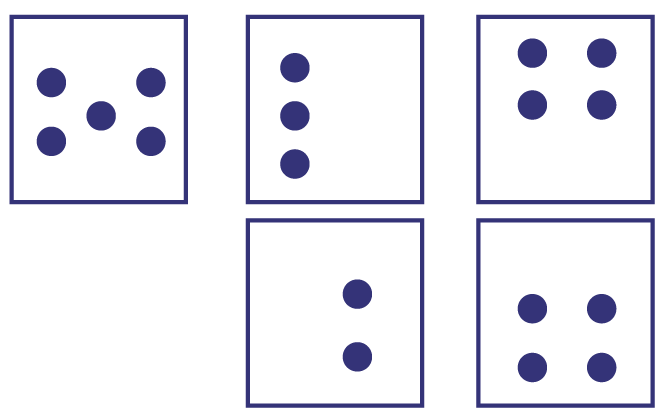
Source: Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 46.
Anchors of 5 and 10
Students become aware of number relationships as soon as they begin to count on their fingers. At this point, students discover the relationships between the numbers 1-4 and the number 5, and the numbers 1-9 and the number 10. Understanding these relationships helps them to recognize, for example, that in a ten frame where tokens have been placed on all but one square, the number 9 has been represented.
This understanding is later extended, first to the relationships between the numbers 0-10 and the anchor points 5 and 10, and then to larger numbers.
Understanding the relationships between numbers and the anchors of 5 and 10 helps students better grasp the concept of place value. By grouping interlocking cubes or centicubes, students discover the relationships between ones and tens and between tens and hundreds. It is important to note that all of these manipulatives help students develop their understanding of place value as long as they have the opportunity to use them in well-structured activities. There is no point in simply modelling the use of the materials without giving students the opportunity to manipulate them and develop the concept on their own. This would be like making them learn an algorithm by heart without understanding it.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 63-64.
Skill: Representing Whole Numbers
Students need to learn to represent numbers in a variety of ways and to recognize them in their multiple representations. These skills help them make connections between a number, its representation, and the quantity it represents. It is therefore essential that students be exposed to different representations of numbers and to a variety of contexts that lead them to represent a number in each of the representations shown in the diagram below, as well as to move from one representation to another.
Teachers need to be aware of the order in which they use these four modes of representation with students. Baroody and Coslick (1998, pp. 3-8 to 3-16) suggest that a new concept be presented in a real and meaningful context so that students can first create representations using words, followed by concrete and semi-concrete representations. Only when students have developed some understanding of the concept can they move on to its symbolic representation. Students should be able to make connections between representations and move easily from one representation to another.
Representations Using Words
In Grade 3, students learn to read and write numbers up to 1000 in words. The challenges of writing numbers in words should not be underestimated. To help students overcome these challenges, teachers should include numbers on the word wall and build with them reference materials that summarize the rules of agreement in numbers of 20, 100 and 1000..
Concrete Representations
Using manipulatives (for example, tokens, base ten materials) to represent numbers helps students develop number sense.
A word of caution is in order when it comes to using manipulatives. It is important to recognize that the materials represent a mathematical concept, not the concept itself; for example, the flat is not a hundred, but it represents a hundred small cubes.
The danger is that students will use the manipulative mechanically without making the connections to the underlying mathematical concepts. For this reason, teachers must ensure that there is real learning and not just blind use of the model. For example, it is easy for students to fill in the blanks in the sentence below the picture by looking at the place value mat.
The representation is ____ hundred(s), ____ten(s) and ____ one(s).
But do students understand that there are also 235 ones units on the mat, and that this is one of the realities that is represented by the number 235? It is important to ask students to explain in different ways what is represented. For example, 235 is also 23 tens and 5 units or 2 hundreds and 35 units.
Another way to check for understanding is to ask students how many tens there are in 235. Many students will tend to say that there are 3. It is important to clarify that the number in the tens position is a "3", but that the number 235 is made up of 23 tens (23 groups of 10 units = 230). These 23 tens can be "seen" by breaking down the 2 flats into 20 rods and adding them to the 3 rods that are in the tens column.
Using the place value mat, we notice that even though numbers are written from left to right, they are formed from right to left: ones grouped together form tens, tens grouped together form hundreds, and so on. But, once the counting is finished, we write the number starting from the left.
The choice of materials available to students can also make a difference in the level of understanding of concepts. There are a variety of materials on the market to represent numbers: marbles, interlocking cubes, or any other object that can be used to count. Some of these materials clearly and concretely represent the magnitude relationship between ones, tens, hundreds… (for example, the base ten material used in the previous photos). However, with other materials, this relationship is represented in a more abstract way. For example, on an abacus or a place value flip board, the grouping is represented according to the position of the digit from left to right, as in symbolic writing of numbers.
By exposing students to a variety of manipulatives, teachers can help them develop a better understanding of numbers.
Semi-Concrete Representations
Students can also represent numbers using semi-concrete materials (for example, illustration, number grid, number line).
Illustration: A number can be represented by drawings in order to illustrate certain groupings. For example, the number 176 can be illustrated in groupings of 50 as follows:
The drawings can also be related to manipulatives.
Number Grid: The number grid to 100 is widely used in the primary grades. Although more difficult to manipulate, a grid of 1000 can help students in the primary grades to better understand numbers by allowing them to compare and contrast them.
Number Line in the primary grades, students use and construct number lines to count in intervals or to identify the number of tens in a number. Using and constructing a variety of number lines allows students to represent large numbers and recognize relationships between them. The following are examples of number lines on which the number 457 is represented:
- number line scaled in intervals of 250;
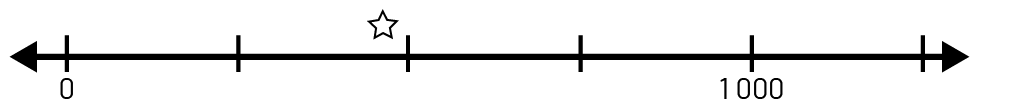
- number line that does not start at 0, whose scale is by intervals of 20;
- an open number line (not scaled) on which numbers are placed in relation to each other;
- a vertical number line that presents numbers in ascending order upward and makes connections to other strands including Spatial Sense (for example, thermometer) and Data (for example, y-axis).
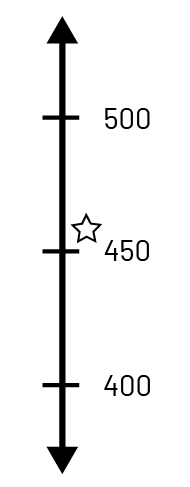
Symbolic Representations
Numbers are represented symbolically by the digits that make them up.
Writing large numbers requires a good grasp of the concept of place value, otherwise a student asked to write symbolically "513" might write 500 13. It also requires an understanding of the identity rule to indicate the absence of a quantity in one of the positions.
A number can be represented in a variety of ways using mathematical symbols, either by respecting the place value of each digit (836 equals 800 + 30 + 6), or by a few place values (836 equals 83 tens and 6 units), or by performing different operations (836 equals 800 + 36, or 840 - 4, or 800 + 10 + 10 + 6). In fact, there are an infinite number of ways to represent a number, each of which allows students to develop a different way of interpreting it and understanding its meaning.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 64-71.
Skill: Composing and Decomposing Whole Numbers
Decomposition and combining are reciprocal notions related to the concepts of final, initial, added or united quantities. Decomposition implies that a final quantity can be decomposed into different initial, added, united or compared quantities. Combining, on the other hand, implies that different initial, united or added quantities can be combined together to form a final quantity.
Over time, students develop an understanding of the concept of quantity and the structure of numbers in base ten. Students are then able to understand that a number can also be decomposed based on place values (for example, 125 can be decomposed into 1 hundred, 2 tens, and 5 ones) and that, conversely, it is possible to group the elements of a set into tens or hundreds in order to determine the number of elements (for example, grouping the elements of a set into 1 hundred, 2 tens, and 5 ones, and concluding that the set contains 125 elements).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 47.
Therefore, it is important to provide students with many activities involving decomposing numbers into tens and ones to help them grasp the concept of quantity related to place value.
Skill: Describing the Ways in Which Numbers are Used in Everyday Life
To understand the concept of a number, connections must be made between the symbol (for example, 684), the word (for example, six hundred and eighty-four), the quantity (for example, 684 objects), or the position (for example, the684th chair in an auditorium). Numbers are also sometimes used as a simple code, without reference to quantity or position (for example, 4 in a phone number or on a soccer jersey). Adults, who have long understood that the meaning of numbers depends on the context in which they are used, are often unaware of the difficulty children may have in grasping these differences.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 73.
Knowledge: Whole Numbers
A positive number, including zero, that has no decimal or fractional parts; for example, 0, 1, 2, 3, 4, 5, ....…}.