B1.7 Represent and solve fair-share problems that focus on determining and using equivalent fractions, including problems that involve halves, fourths, and eighths; thirds and sixths; and fifths and tenths.
Skill: Finding and Using Equivalent Fractions in Solving Fair-Share Problems
The notion of equivalent fractions is introduced in grade 1. However, it is sometimes difficult for students to grasp that a quantity can have several names and be represented by several numbers (for example, the number \(1 \frac{2}{3}\) represents the same quantity as the number \(1 \frac{4}{6}\); therefore, we can say that \(1 \frac{2}{3} = 1 \frac{4}{6}\)).
Understanding equivalent fractions is part of the proportional reasoning that students will continue to develop in the junior and intermediate divisions.
To determine equivalent fractions is to determine fractions that represent the same quantity. We then seek a number of “small parts” of a whole which correspond to a particular number of “large parts” of the same whole. For example, if we find the number of eighths that corresponds to a quarter (\(\frac{1}{4} = \frac{\mathord{?}}{8}\)):
\(\frac{1}{4}\) of a chocolate bar
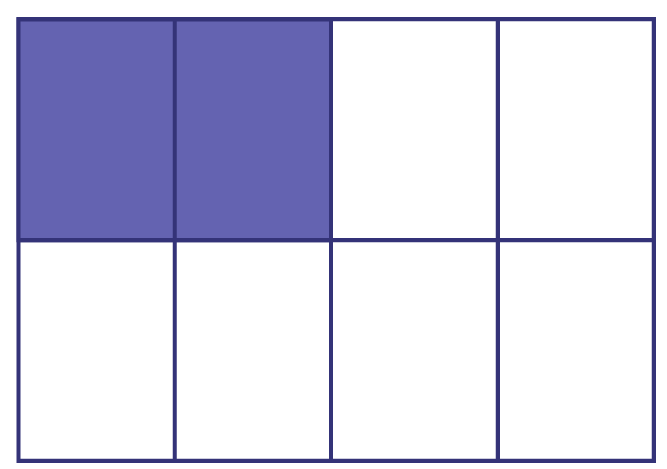
\(\frac{2}{8}\) of the same chocolate bar
The equivalence relation must also be explored with respect to fractions of a set. In the image below, students can easily see that \(\frac{6}{10}\) candies are wrapped in purple foil.
However, they have difficulty determining other equivalent fractions. It is important to introduce activities that allow them to manipulate the elements of the set. This way, students can group them into sets of 2 and determine equivalent fractions.
\(\frac{3}{5}\) of the candies are wrapped in purple foil
Concrete experience with equivalent fractions is the foundation of proportional reasoning. It cannot be overemphasized. Therefore, teachers should plan activities that build on the informal concepts related to equivalent fractions.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-53.
Models and tools can be used to develop an understanding of equivalent fractions.
Examples
- Fraction strips or other models, such as fractional circles, can create the same area as the original fraction when we use fractional or joined parts.
- Strips of paper can be folded to show the fractioning to create equivalent parts.
- A double number line can be used to represent equivalent fractions based on different scales.
Source : Ontario Mathematics Curriculum Grades 1-8, 2020, Ministry of Education of Ontario.
Skill: Representing Fractions in Various Contexts
Context is all the information surrounding a situation. In the study of fractions, the whole is an essential part of the context. When solving contextual problems, a fraction such as \(\frac{2}{3}\) does not provide enough information to understand the quantity referenced without "the whole" being defined. For example, when we hear "one half", we usually think of a small quantity. However, we need to consider this quantity in context since the context may lead us to form different opinions about the same fraction. Eating half an apple at snack time is a little; eating half a pie is a lot; if half the students in the class are absent, it is a lot. As with whole numbers, context is essential for making informed decisions about the size of the quantity represented by a fraction. It is important that students learn to always consider the whole. When analysing a situation, a fraction is meaningless if it is not related to a whole. For example, we cannot compare one half of a pizza to one third of a pizza unless the two pizzas are the same size. Teachers should provide learning situations that allow students to understand that a fraction does not reveal anything about the size of the whole or its parts; it only tells us about the relationship between a whole and its parts.
In any situation, the whole corresponds to an element or a set of elements.
If the whole corresponds to an element, it can be split into equivalent parts. Each of the parts can then be compared to the whole.
Examples
If the whole corresponds to a set of elements, namely a collection of objects, some of the elements can be grouped together to form a part of the set and thus represent a part of the whole.
Examples
In general, when it comes to fractions, we refer to 3 different models: the set model, the linear model and the area model.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-32.
Knowledge: Equivalent Fractions
Different fractions can represent the same quantity. \(\frac{5}{10}\), \(\frac{4}{8}\), \(\frac{3}{6}\) and \(\frac{2}{4}\) all represent the same quantity, or one-half of the same whole. Fractions are considered equivalent when they represent the same number or quantity.
When 2 fractions are equivalent, the relations between the numerator and the denominator are constant. For example, in \(\frac{1}{2}\) and \(\frac{2}{4}\), the denominator in both fractions is twice the numerator, and the numerator in a fraction is twice the other, just as the denominator of one is twice the other.
Source : Ontario Mathematics Curriculum Grades 1-8, 2020, Ministry of Education of Ontario.