B2.1 Use the properties of operations, and the relationships between multiplication and division, to solve problems and check calculations.
Skill: Using Properties of Operations to Solve Problems and Check Calculations
Students demonstrate understanding of the properties of mathematical operations with specific objects or numbers. Students use concrete materials, drawings, words, or symbols to represent mathematical ideas and relationships.
It is not necessary for elementary students to know the names of the properties. They just need to use them naturally to combine numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 33.
Commutative Property
Addition and multiplication are commutative. For example, we can demonstrate the commutative property of addition as follows:

We then recognize that if the terms of an addition are interchanged, the result remains the same.
We can also demonstrate the commutative property of multiplication. For example, 8 x 3 and 3 x 8.

The two previous layouts represent the same total quantity, organized in two different ways. As a result, they illustrate two different situations. Thus, \(8 \times 3\) represents 8 rows of 3 objects, while \(3 \times 8\) represents 3 rows of 8 objects. It is important that students recognize the different representations.
An example from everyday life can also be used. For example, the teacher invites three students who have exactly one sibling to come up to the board to represent the number of children in their family. The total number of children is represented by 2 x 3 children, for a total of 6 children (Figure 1).
Then, teachers do the same with two children who have exactly two siblings. The total number of children is represented by 2 x 3 children, for a total of 6 children (Figure 2).
Figure 1

Figure 2

The two number sentences, \(3 \times 2 = 6\) and \(2 \times 3 = 6\), indicate the same result, even though the order of the factors is changed. The students can then understand that 3 families of 2 children or 2 families of 3 children give a total of 6 children, without the situations being identical.
When first learning multiplication, students often recognize and understand multiplication as repeated addition. As they attempt to solve a variety of problems, they can begin to see and use the commutative property of multiplication to develop a more efficient computational strategy.
For example, students using repeated addition would recognize that \(2 \times 12 \ (12 + 12)\) is simpler and takes less time to represent and calculate than \(12 \times 2 \ (2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2)\).
An array is an excellent visual model for representing the commutative property of multiplication.

Associative Property
The associative property of multiplication (for example, \(3 \times 2 \times 5 = 3 \times (2 \times 5)\) or \(3 \times 2 \times 5 = (3 \times 2) \times 5\) is not easy to understand. Certainly, it can be seen by checking the results of the multiplications, but this does not constitute an understanding. To understand, one can use an extension of the model of an array using cubes.
In figure 1, we see that there are 2 rows of 5 cubes, that is \(2 \times 5\) cubes. In Figure 2, we see 3 levels each containing \(2 \times 5\) cubes. The figure therefore represents \(3 \times (2 \times 5)\) cubes.

We can also consider Figure 3, which illustrates 3 levels of 2 cubes, that is \(3 \times 2\) cubes. Figure 4 can then represent \(3 \times 2\) cubes which appear 5 times, that is to say \((3 \times 2) \times 5\).
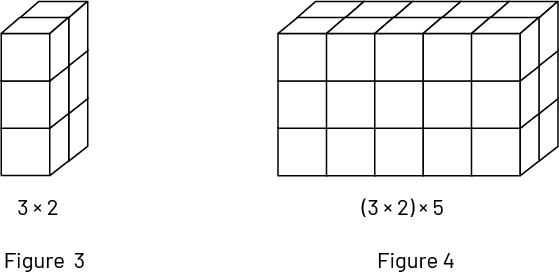
So we see that \(3 \times (2 \times 5)\) and \((3 \times 2) \times 5\) represent the same quantity of cubes (even though each expression represents a different point of view) and that each gives the same product as \(3 \times 2 \times 5\).
Faced with a numerical expression such as \(3 \times (2 \times 5) = \mathord{?}\), some students sometimes try to apply the distributive property in order to calculate \((3 \times 2) \times ( 3 \times 5)\), which has the effect that \(2 \times 5\) is multiplied by 9, rather than by 3. In such a case, remember that the distributive property says that multiplication is distributed over addition or subtraction and explain the situation using a concrete or semi-concrete model.
The associative property does not change the order of numbers in a numerical expression. However, the associative property and the commutative property can be combined to facilitate the evaluation of a numerical expression.
For example, to determine the value of the expression \(2 \times 3 \times 5\), one can determine the value of the expression \((2 \times 5) \times 3\). Indeed, it is usually easier to calculate \(10 \times 3\) than to calculate \(6 \times 5\).
The Distributive Property
The following example illustrates how the distributive property can be used to calculate \(6 \times 8\). In one case, we decompose the factor 8 to obtain \(5 + 3\). We then have \(6 \times (5 + 3) = (6 \times 5) + (6 \times 3)\). In the other case, we decompose the factor 6 to obtain \(3 + 3\). We then have \((3 + 3) \times 8 = (3 \times 8) + (3 \times 8)\).

Only multiplication is distributive over addition or subtraction. One could recognize that division is partially distributive. For example, to calculate \(32\; \div \;8\), it is possible to decompose the dividend 32 to obtain \(16\; + \;16\). We then have \((16\; + \;16)\; \div \;8\) and the division by 8 is distributed over the addition. We get \((16\; \div \;8)\; + \;(16\; \div \;8)\; = \;2\; + \;2\), that is 4. However if the divisor is decomposed, the distributive property does not work. For example, \(32\; \div \;8\; \ne \;\left( {32\; \div \;4} \right)\; + \;\left( {32\; \div \ ;4} \right)\). This is the reason why distributivity is not a property of division.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 102-106.
Sometimes a property may be used to check an answer. For example, \(4\; \times \;9\) may be first be determined using the distributive property as \(2\; \times \;9\; + \;2\; \times \;9\) and then checked by decomposing \(4\; \times \;9\) as \(2\; \times \;2\; \times \;9\) and using the associative property \(2\; \times \;(2\; \times \;9)\).
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Skill: Using the Relationships Between Multiplication and Division to Solve Problems
Understanding the relationships between operations allows them to be used more flexibly.
The more opportunities students have to handle operations, the more they can notice and understand the relationships between them. Students may even use addition or subtraction strategies to solve multiplication and division.
In the primary grades, students have made connections between operations through various activities. For example, students know that addition and subtraction are inverse operations and that addition is commutative. Over time, they develop their number sense and sense of operations and gradually use them before performing operations. This practice, while often informal and mental, is still essential to understanding the relationships between numbers and between operations.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 97.
Multiplication and Division
Multiplication and division are inverse operations. They can also be related to the concept of a whole and its parts. In multiplication, parts are combined as equal groups, while in division, a whole is partitioned into equal groups. From this relationship between multiplication and division, students can use the number facts about multiplication to perform division. Students often misunderstand the inverse relationship between multiplication and division, even after performing division and checking their calculations. Therefore, it is essential to regularly revisit the meaning of each operation in a problem-solving context.
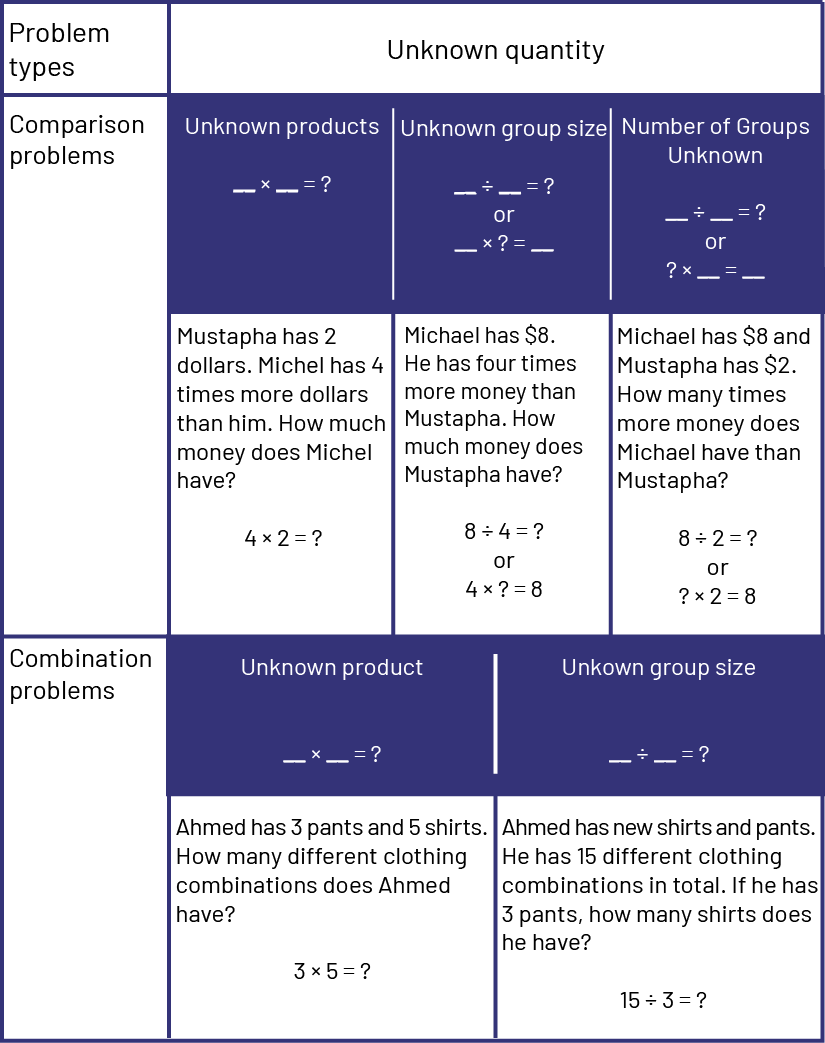
To understand multiplication and division, the 3 types of quantities involved need to be recognized: the total quantity (for example, 8 flowers), the number of equal groups (for example, 4 pots) and the size of each group (for example, 2 flowers per pot).

In problems presented to students, division is too often associated with only one type, namely equal-sharing (partitive division). The equal-grouping type (quotative division) is usually neglected. Division is partitive when the total quantity and the number of groups are known (for example, 3 students want to share 15 apples equally and we are looking for the number of apples each person will receive).
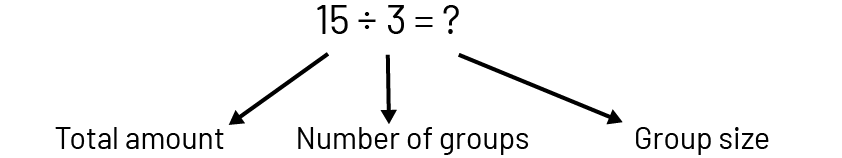
In quotative division the total quantity and the size of the groups are known (for example, we have 15 apples and we want to put them in bags, 3 apples per bag; we look for the number of bags we need).
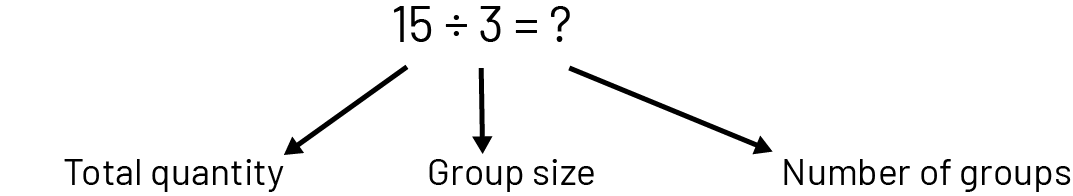
It is essential to address both types of problems, as they are the basis for the integration of other mathematical concepts. It is not necessary for students to know the names of the problem types, but it is essential that they have the opportunity to solve a variety of problem types while using a variety of strategies.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 84-86.
Knowledge: Properties of Operations
A property of an operation is a characteristic that is specific to the operation, regardless of the numbers involved.
The properties of the operations are:
- Commutative Property (3 + 5 = 5 + 3)
- Associative Property: \(\left( {2\; + \;9)\; + \;11\; = \;2\; + \;(9\; + \;11} \right)\);
- Distributive Property: \(8\; \times \;7\; = \;\left( {8\; \times \;5} \right)\; + \;\left( {8\; \times \;2} \right)\);
- Identity Rule: \(13 + 0 = 13\), \(0 + 13 = 13\); \(25 \times 1 = 25\), \(1 \times 25 = 25\)
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 102.
Knowledge: Commutative Property
An operation is commutative if its result remains unchanged when the order of its terms or factors is reversed. Addition and multiplication are commutative. For example, \(27\; + \;63\; = \;63\; + \;27\) and \(8\; \times \;6\; = \;6\; \times \;8\).
Knowledge: Associative Property
The associative property of addition and multiplication allows you to regroup the terms or factors of an expression in different ways without changing the value of the expression.
Knowledge: Identity Property of Addition and Identity Property of Multiplication
The Identity Property of Addition states that when adding 0 to any amount, the amount stays the same (for example, \(287 + 0 = 287\), \(4.5 + 0 = 4.5\). The Identity Property of Multiplication states that when multiplying an amount by 1 or dividing an amount by 1, the amount stays the same (for example, 133 × 1 = 133, 432.1 × 1 = 432.1) .
There is no identity property for either subtraction or division. However, there is a Zero Principle for Subtraction which states that 0 subtracted from any number results in the same number, that is, n – 0 = n. Note: The number 0 has no effect when it is the 2nd term (\(3 - 0 = 3\)), but this is not the case if it appears as the 1st term (\(0 - 3 \ne 3\)). Similarly, The Identity Property states that when dividing an amount by 1, the amount stays the same (for example, 3 ÷ 1 = 3). The number 1 has no effect when it is the divisor. Again, we must make clear to students that since division is not a commutative operation, we cannot then assume that the number 1 has no effect when it is the dividend (for example, \(1 \div 3 = 0.3\)).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 107.
Knowledge: Relationships Between Addition, Subtraction, Multiplication and Division
- Addition and subtraction are inverse operations.
- Multiplication can be associated with repeated addition.
- Division can be associated with repeated subtraction.
- Multiplication and division are inverse operations.
