B2.4 Demonstrate an understanding of algorithms for adding and subtracting whole numbers by making connections to and describing the way other tools and strategies are used to add and subtract.
Skill: Demonstrating an Understanding of Algorithms for Adding and Subtracting Whole Numbers
To promote mastery of mathematical operations, it is important to emphasize the efficiency and flexibility with which algorithms must be used. Students who approach numbers with flexibility are more likely to use efficient strategies, work with precision, and develop a solid foundation for understanding other common algorithms. Studies have repeatedly shown that it is very helpful for students to have many opportunities to develop their own multi-digit number strategies (Morrow & Kenney, 1998).
In the past, many people assumed that there was only one way to perform an operation, which was likely one they learned in school. Cultural differences in how such operations are performed, however, indicate that algorithms can have many variations. Adults often think that the algorithm they have been taught is the only one possible. In reality, there are different algorithms to perform an operation. The following box gives some examples of the different ways to solve \(27 + 48\) using variations of the standard North American algorithm.
Each algorithm has a different level of abstraction. Some have more explicit steps than others and some are faster, but more abstract way to get to the answer.

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 34-35.
Teaching Algorithms
It is very important that students have many opportunities in Grade 3 to develop the skills necessary to perform computations using the concepts of combining, the anchors of 5 and 10, and basic number facts up to 20. The experience that early primary students gain with decomposing numbers into ones, tens, and sometimes hundreds will help them make the connection between these basic concepts and multi-digit number operations.
Using pictures, language (spoken and written), and numbers to communicate their computations helps students make connections between the concrete, visual, and abstract levels of their understanding of number operations. Premature presentation of abstract symbols (for example, the = sign) without connecting such symbols to the concepts they represent (for example, the = sign represents equivalence or balance) is often the source of students' difficulties in computation. Rather than searching for the meaning of the operation, they begin to see mathematics as a series of routine rules and procedures with little application to everyday problem solving. The experiences students have should allow them to make sense of the algorithms and develop efficient strategies that can be generalized.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 39.
Flexible Algorithms
In the classroom, it is suggested that several algorithms for a single operation be examined. It is essential that students understand the reasoning behind the actions in these algorithms. Over time, this allows them to choose an effective strategy depending on the context. Teachers with culturally diverse students in their classrooms can invite them to discuss at home the strategy their parents use to perform addition or subtraction. These students can present these strategies to the class, which can provide new ways of doing.
Standard algorithms are often regarded as the most valued computational strategy. Although effective, they are not always appropriate. When the teaching focuses on the standard algorithm, for example, to calculate \(300 - 15\), the students tend to take out a pencil and paper and perform the written algorithm with its trades, which are a common source of errors. However, it would be more efficient to calculate mentally as follows: \(300 - 10 = 290, \ 290 - 5 = 285\). Moreover, the standard algorithm is not the best strategy to use where an estimation is sufficient. This is why it is suggested to consider the standard algorithm as a computational strategy among many others.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 119.
Students can perform computations in a variety of ways. The following are examples of addition and subtraction algorithms. These are not the only ways to solve a problem, so students should be given opportunities to reason about other ways as well.
Examples of Addition Algorithms
\(566 + 379\)
The student proceeds in steps and decomposes the second addend so as to work with friendlier numbers.

The student decomposes the addends horizontally and recomposes them using place value.

The student combines the hundreds, tens and ones.

The student uses a compensation technique.
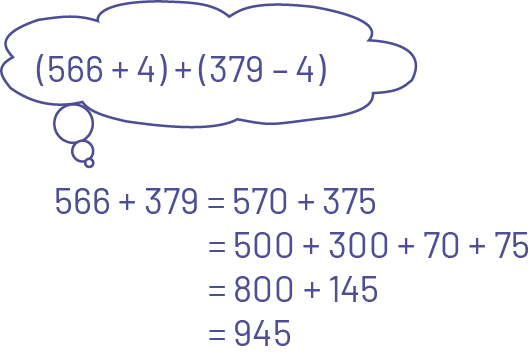
Source: translated from Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 3, Série 2, Activité 2 - Les clients de l'usine Aux mille délices, p. 432.
Examples of Subtraction Algorithms
\(631 - 439\)
The student decomposes the second term and then subtracts it in steps.

The student adds to subtract.
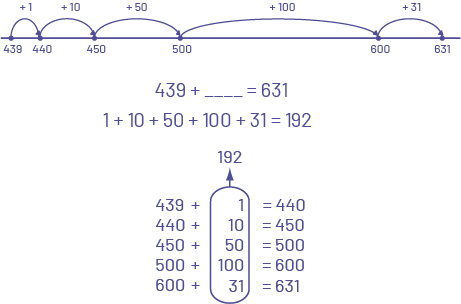
The student decomposes the first term and then subtracts the second term in steps.

The student uses an open number line and records their movements.
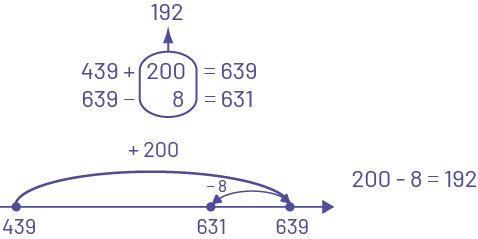
The student uses an open number line, starts at the greater number (minuend), and counts backwards the amount of the lesser number (subtrahend), using place value.
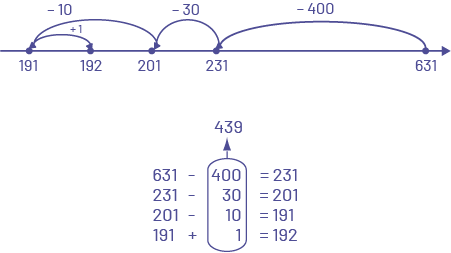
Source: Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 3, Série 2, Activité 4 - Dans l'entrepôt de l'usine, p. 450.
Students can use the principle of compensation that follows from the equality relationship. This involves changing the terms of an operation without changing the result. The principle of compensation involves the conservation of the equality of quantities in operations between numbers.
Compensation is a mental mathematics strategy in which part of the value of one number is given to another number to make computation easier. For example, 26 + 99 can be thought of as 25 + 100; that is, 1 from the 26 is transferred to the 99 to make 100. Compensation sometimes takes place at the end of the computation. For example, 26 + 99 can be thought of as 26 + 100 = 126; and since 1 too many was added, take 1 away to get 125.
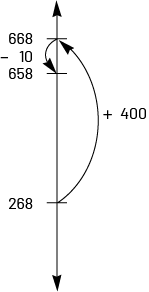
In the following example, we add 10 to the number 390 to get the number 400, which is easy to add. We then subtract 10 from the resulting answer.
\(268 + 390 = \mathord{?}\)
\(268 + 400 = 668\)
\(668 - 10 = 658\)
Therefore, \(268 + 390 = 658\)
You can visualize the situation using a vertical number line. We see that in this case, a number greater than that of the 390 (400) has been added (+10). We must therefore compensate by subtracting the excess (-10).
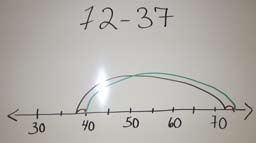
Compensation also applies to subtraction. Since we are looking for the difference between the terms, we modify the two terms in the same way to keep the same difference. We can add the same quantity to both terms or we can subtract the same quantity from both terms. For example, to calculate 72 - 37, we can add 3 to 72 to get a more familiar number, 75, while adding 3 to 37 to keep the same difference.
\(72 - 37 = (72 + 3) - (37 + 3)\)
\(72 - 37 = 75 - 40\)
\(72 - 37 = 35\)
For this same expression, we could also compensate by subtracting 2 from each term.
\(72 - 37 = (72 - 2) - (37 - 2)\)
\(72 - 37 = 70 - 35\)
\(72 - 37 = 35\)
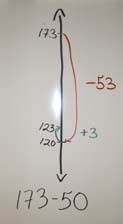
We can also use compensation to subtract a larger number than is required in the mathematical expression and then add to the difference. In the following example, we subtract 53 (3 more than needed) to make the subtraction easier. We then add 3 to the result to compensate.
\(173 - 50 = \mathord{?}\)
\(173 - 53 = 120\)
\(120 + 3 = 123\)
So \(173 - 50 = 123\)
Compensation in subtraction uses the principle of constant difference, that is, the difference between two numbers is the same if you add or subtract the same amount from them (for example, the difference between 645 and 185 is the same as the difference between 650 and 190 or the difference between 640 and 180).
The concept of constant difference can be used to perform operations such as subtraction with 0's (for example, 1000 - 354 = 999 - 353.

Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 91-101.
The examples above give an idea of the different approaches students might use to develop their own algorithms. It is important to remember that using an algorithm is an efficient and effective way to perform a mathematical operation. The algorithms that students create are not necessarily efficient and effective. Some may, for example, require more steps and more time than necessary. However, students develop such algorithms because they make sense to them. As students share and compare their strategies, they find increasingly efficient and effective methods. An efficient method is one that requires few mathematical operations and little time to arrive at the answer. An effective method is one that is applicable to all questions of this type, in other words, it is generalizable to questions within the same operation.
For young students, learning multi-digit number operations can be a positive or negative introduction to the more complex and formal mathematics they will be taught in later years. Multi-digit number operations are often a source of frustration for students who have difficulty seeing the connections between mathematical operations and problem solving. A balanced approach using guided, shared, and independent learning is important for teaching these operations and giving students a chance to understand and use them.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 45.
Standard Algorithms
Although student-created algorithms allow students to develop mathematical strategies that work for them, most people are more accustomed to the standard North American algorithm that they were taught in school. It is only after students have developed a sense of number and a good knowledge of personal strategies for performing basic mathematical operations that they should be introduced to the standard algorithm. When introducing students to standard algorithms, it is important to help them develop a good understanding of operations rather than simply asking them to memorize rules. Some students will prefer to use the standard algorithm, while others will continue to use the flexible strategies developed in class.
Several considerations should be taken into account when introducing standard algorithms to students:
Prior Learning - Students must have had multiple experiences that allowed them to develop flexible algorithms to perform an operation.
Mathematical Language – Terms like “borrowing” and “withholding” are misleading. It is preferable to speak of “exchange and regroup” or "decomposing and composing". Special attention should be paid to how to name the tens digit in a 2-digit number when describing an operation. It happens that students fall into the trap and name the tens digit by its simple digit term. So instead of saying "Subtract 20 from 30" to explain the answer to a problem like \(35 - 22\), these students say "Subtract 2 from 3". This creates a conceptual misunderstanding that is likely to persist, especially when students are working with more complex numbers, such as decimals (junior students often have difficulty determining whether the answer to a problem is 0.32; 3.2 or 32.0).
Place Value - Most standard algorithms involve combining by tens, hundreds and so on. Students need to use manipulatives in activities that involve combining to fully understand place value.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 54-55.
When deciding whether to use the standard algorithm or a flexible algorithm, always consider the situation and the numbers being used. For example, when giving change for a purchase at the store, using a flexible algorithm that counts from the cost of the purchase to the amount paid by the customer is much more efficient than the standard algorithm, at least for subtractions of multi-digit numbers. Similarly, it is probably not necessary to use the complex steps taught in the standard algorithm to perform a calculation such as (1000 - 10); a simple countdown by 10 will give the fastest answer for anyone who knows what they are doing and why. On the other hand, to perform a calculation involving several numbers, it may be more appropriate to use the standard algorithm and do the calculation on paper.
Strategies to Facilitate the Understanding of Standard Algorithms
It is important to provide students with several activities to explore standard algorithms using manipulatives such as the place value mat, interlocking cubes, ten frames, base ten materials, number lines, etc.
Teachers need to provide students with many opportunities to create their own algorithms, to explain their strategies and the reasons for their choices. It is important to give students the opportunity and time to explore the algorithms in greater depth and to encourage discussion. It is important to encourage students to work in pairs (one student writes down the steps while the other works with the concrete representation). Understanding of the meaning of the steps in a standard algorithm develops when teachers allow students to compare it to their own algorithm in order to make connections between the two approaches, such as "add from left to right and combine".
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 56.
Adding Multi-Digit Numbers Without Combining
Addition of large numbers can be represented on a number line. For example, students could perform \(435 + 223\) by decomposing 223 (\(200 + 15 + 8\)) and representing the operation as follows:


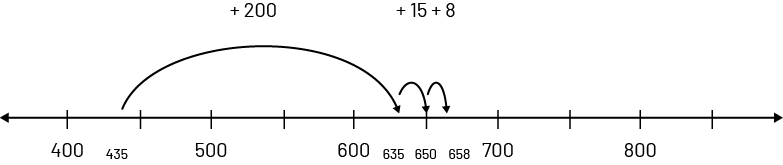
Over time, students gradually develop their sense of abstraction and can use the same strategy without using a number line, but by performing the calculation mentally.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 122-123.
Adding Multi-Digit Numbers by Combining
(Van de Walle and Folk, 2005, p. 191)
It is important for students to practice combining groups of 10 ones (units) into tens, groups of 10 tens into hundreds, and so on. They need the support of visual representations of combinations to develop a conceptual understanding of the algorithm.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 57.
Base ten materials help some students visualize the operation more clearly. Here is how base ten materials can be used to represent addition.
Example
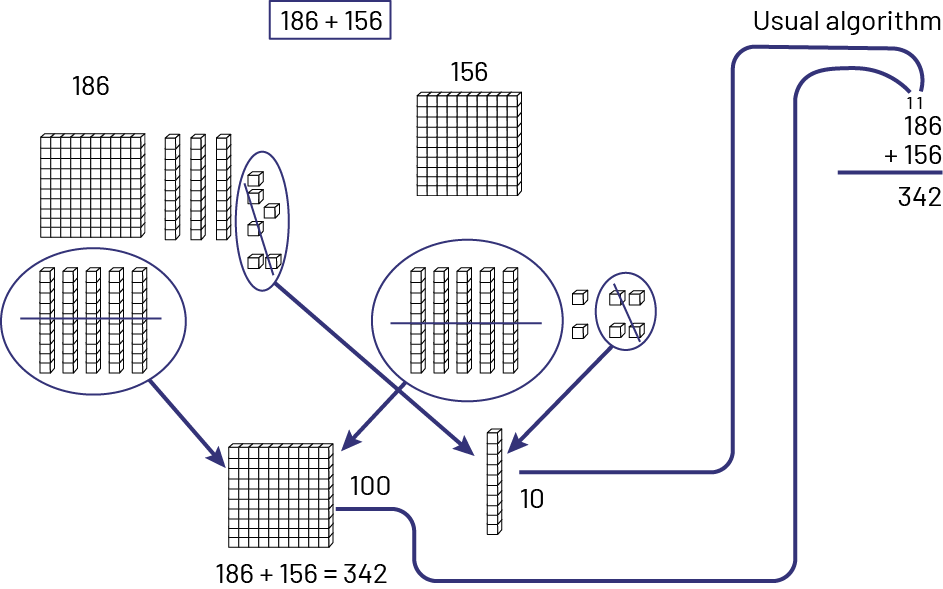
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 123.
Subtraction Without Regrouping
As with addition, students often use manipulatives to perform subtractions. This strategy helps them grasp the concept of separation or removing another quantity, although it is not very effective when dealing with large numbers.

Base ten materials allow students to perform subtraction using separation.
Example
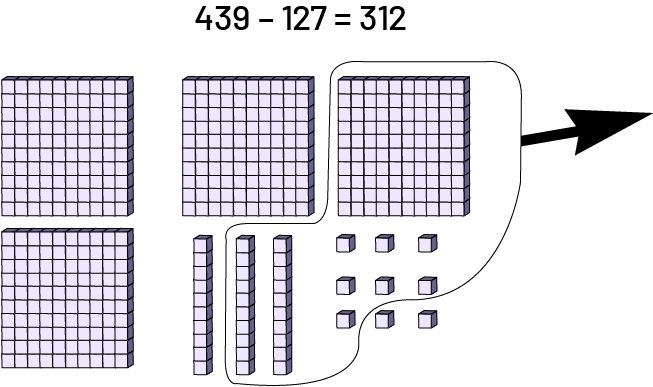
If the place value mat for subtraction is used, some students tend to represent both terms. The subtraction is then performed by comparison to find the difference between the two terms.
Example

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 127-128.
Subtraction With Regrouping
(Van de Walle and Folk, 2005, p. 191)
Exploring subtraction with regrouping promotes conceptual understanding. Teachers should encourage students to use the place value mat and base ten materials to model subtraction with regrouping. Students can work in pairs. They can move on to the written form of the algorithm once they have developed a solid understanding through modelling.
In the case of the calculation \(325\; - \;118\), students represent the first number (325) with base ten materials on the top portion of the place value mat. They cannot remove 8 ones since there are only 5 of them, so they need to decompose one ten for 10 ones.


This gives them a group of 15 ones from which they can now remove 8 so that 7 ones remain. Students should be encouraged to group the ones on the mat to better organize their work.
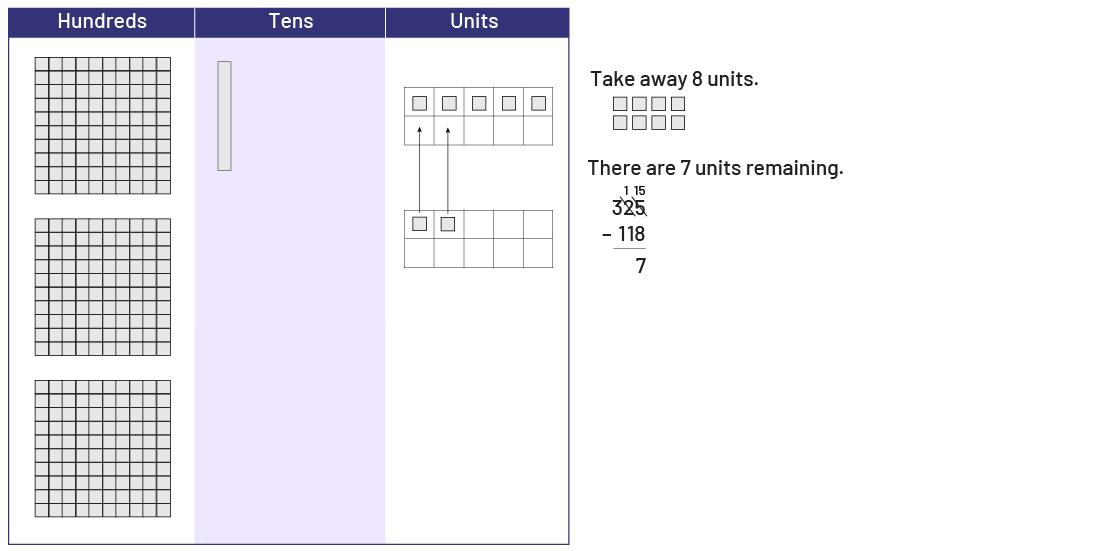
Students now remove 1 ten and 1 hundred and place them outside the mat.
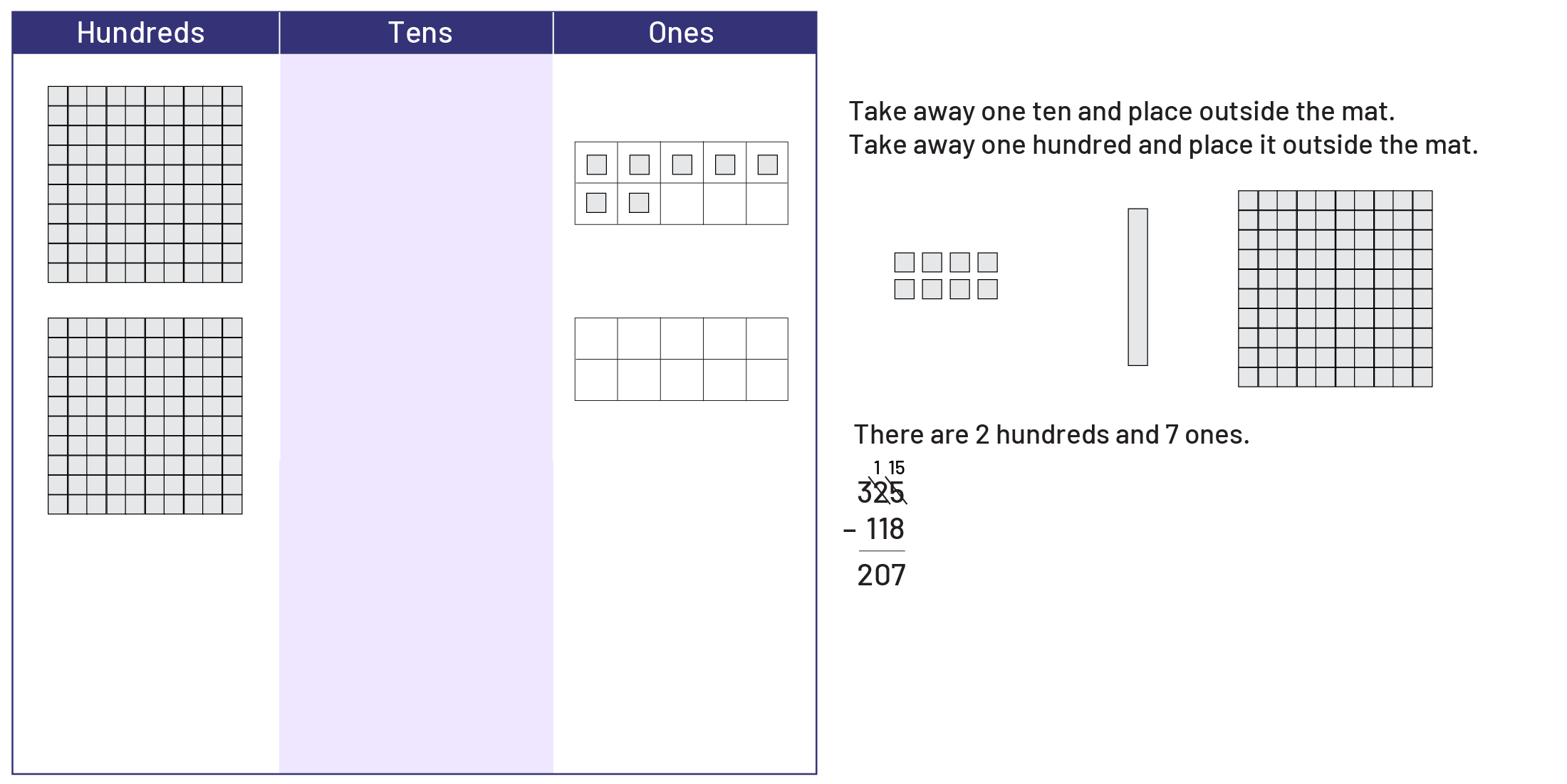
So \(325 - 118 = 207\).
Students can also use the number line to perform a subtraction. For example, to calculate \(263\; - \;45\), they can use compensation to work with more familiar numbers. Since \(263\; + \;2\; = \;265\), we can perform \(265\; - \;45\; = \;220\) and then subtract 2 to compensate \((263\; + \;2\; - \;45\; - \;2)\).
Students do not have to transcribe their thinking into numerical expressions, but can use the number line to illustrate their thinking:
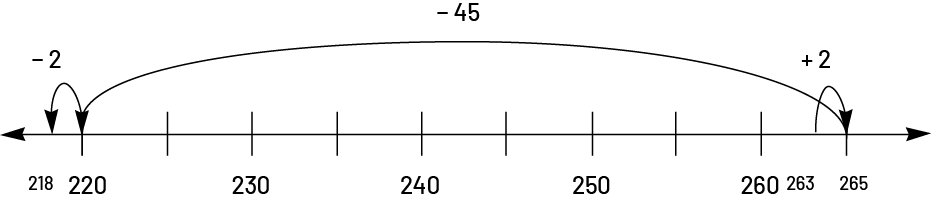
The number line can also be used with the decomposition according to the place values of the digits of the number (\(263 - 40 = 223\), \(223 - 5 = 218\)):
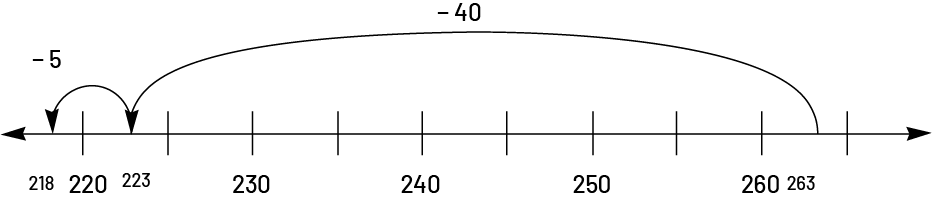
The open number line allows students to proceed in significant leaps (\(263 - 3 = 260\), \(260 - 40 = 220\), \(220 - 2 = 218\)):
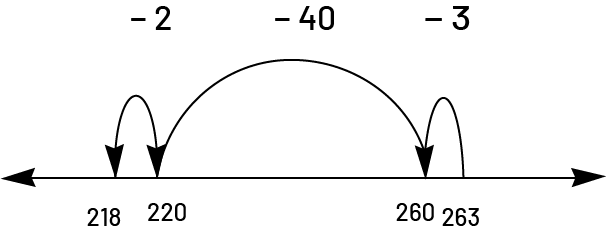
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 127.
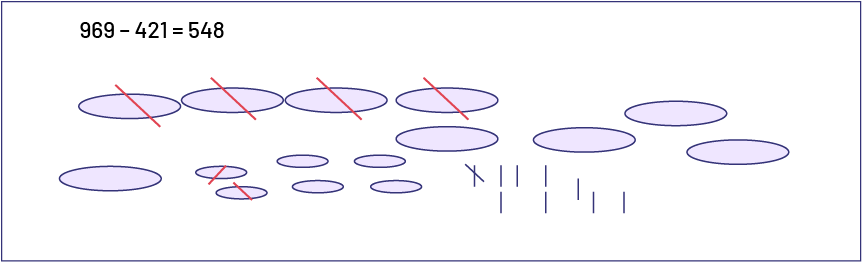
Students can use drawings to quickly illustrate a number expression such as \(969 - 421\). Numbers can be represented by lines, circles, dots, etc. A separation can be expressed by bars on the drawing. For \(969 - 421\), one must remove 4 hundreds, 2 tens and 1 one from the 9 hundreds, 6 tens and 9 ones.