B2.5 Represent and solve problems involving the addition and subtraction of whole numbers that add up to no more than 1000, using various tools and algorithms.
Skill: Representing and Solving Problems Involving Addition and Subtraction
In addition to teaching arithmetic operations using strategies and reasoning, it is important to introduce these operations in problem-solving contexts. In problem solving, students are encouraged to use prior knowledge and make connections to new learning. These connections can be broken if students are not presented with a diverse range of problems. Students who do not learn to calculate in problem-solving contexts may have great difficulty making these connections later. Their understanding of the abstract concept of number and its application may be blurred, and some may not be able to effectively use computational strategies to solve problems.
The use of problem-solving contexts is equally important for multi-digit number operations. When students are given problems, when they are encouraged to come up with an algorithm and use it flexibly, they are given the opportunity to deepen their understanding of operations. In the interest of efficiency and in the belief that it is the right thing to do, students are often taught the algorithm to be used to perform operations on multi-digit numbers. With this method presented as the "right way" to solve the problem, students struggle to understand and remember this procedure. This method often results in inefficient use of the algorithm, lack of accuracy, and limited understanding. If, instead, students are encouraged to make sense of the problem and develop their own strategies for solving it, they will demonstrate more fluency and accuracy in their work with operations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 5.
This will allow them to develop and explore various personal strategies or algorithms.
To develop effective strategies for students, it is important to provide students with a variety of problem types so that they can grasp the multiple meanings of operations. A well-chosen problem and the application of a thoughtful strategy are more beneficial than a series of mechanically completed exercises. Students should be given the time they need to understand and consolidate strategies.
The exploration of strategies (including flexible algorithms) is essential as these are tangible examples of the number sense and operations sense that students have acquired. These strategies and flexible algorithms indicate how they "play" with numbers and operations. These strategies that are put on paper have the potential to translate into mental math strategies. For example, students who have the opportunity to write their reasoning on paper or who use a number chart to perform a calculation such as (36 + 52) may later follow a similar reasoning mentally.
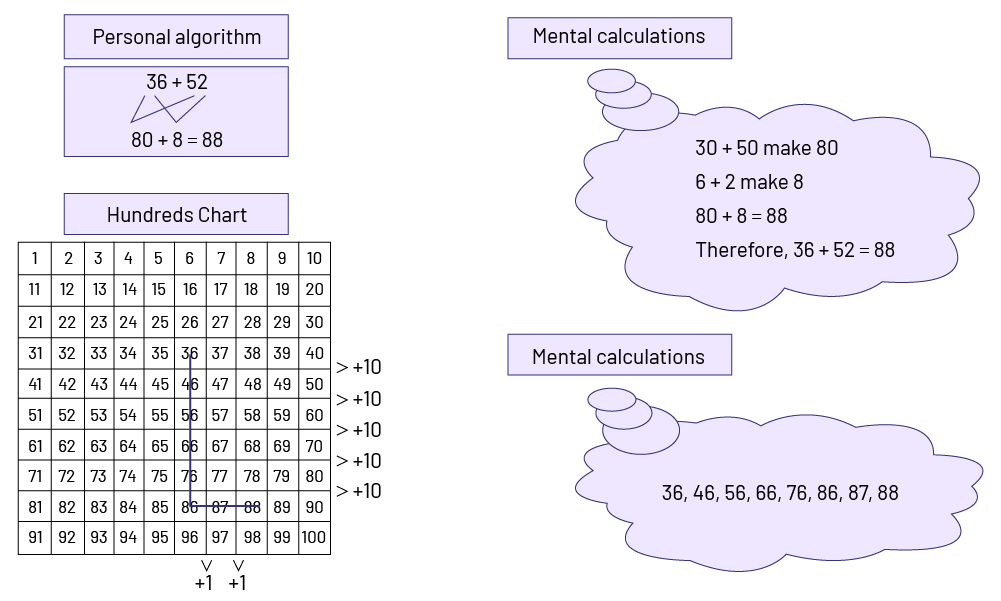
In addition, it is essential to facilitate mathematical discussions about, for example, these strategies and flexible algorithms. These discussions encourage the sharing of strategies and the recognition of connections between them. Each student's personal strategies become clearer, more sophisticated, and more effective as they makes connections between them. In this way, "teachers guide the discussion by using strategies that students have used to initiate understanding of specific mathematical concepts and to direct students' progress towards effective methods" (Ontario Ministry of Education, 2004a, p. 18).
The teacher's role is to help students organize their work. For example, students can be led to use semi-concrete representations, pointing out that a student who has combined objects shows the same reasoning as the student who wrote the number as a combination.
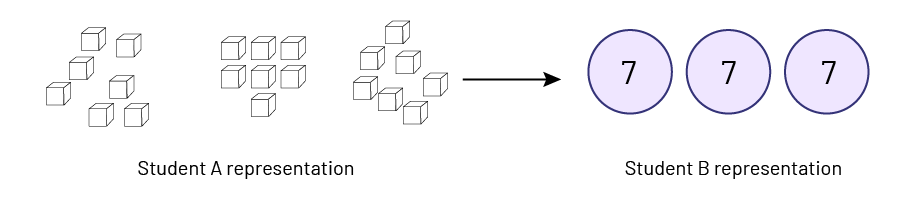
Similarly, when a student physically takes 10 groups of 10 ones, sees that it is a group of 100 ones, and calls it a hundred, it can be mentioned that they are using the concept of combination and that it is the same combination that is symbolized by writing the number "1" above the hundreds place value in the standard algorithm.
Scaffolding by teachers helps students understand the underlying concepts associated with various operations (for example, partitioning in subtraction). In addition, the mathematical exchange makes it possible to present new strategies. Teachers and students can also model strategies by making sure to verbalize the reasoning behind them. Later, the standard algorithm can be presented, ensuring that the students understand the underlying concepts and the reasons for the actions taken. Standard algorithms should be seen by students as just another way of performing operations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 76-78.
Written Problems Involving Addition and Subtraction
In addition and subtraction, quantities are joined, separated, combined or compared. In order for students to understand the connections between quantities in each of these cases, it is important that they be presented with a variety of problem types. Below are a variety of addition and subtraction problems.
Addition and subtraction are simply operations that occur in problems. Therefore, it is important to avoid referring to them as "subtraction problems" or "addition problems" because it is the understanding of the situation, as well as the understanding of the operations, that leads to the choice of a problem-solving strategy, in this case the choice of addition or subtraction. Thus, students must analyze the problem, choose a strategy and apply it, just as adults do. In this context, the teacher's role is to assist students in their analysis and understanding of operations.
It is important to note that the problems presented below appear similar because of their context. However, for students, each situation represents a unique problem. It is through mastery of these different types of problems that students gain mastery of addition and subtraction.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83.
Joining Problems
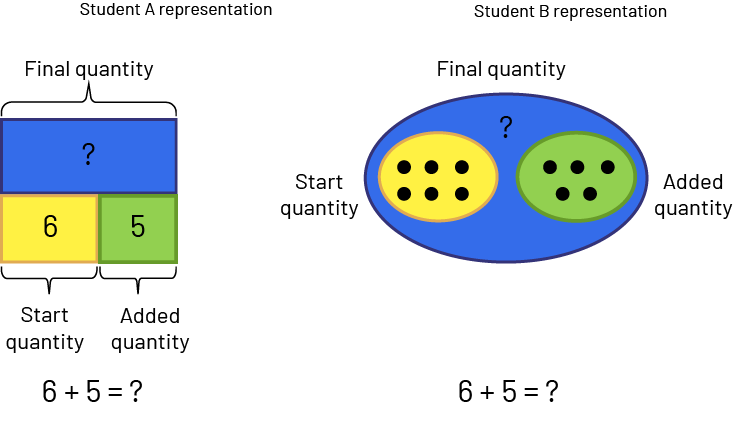
The part-whole model can be useful for representing known and unknown values in joining problems. The set model is useful for representing the joining of a quantity to another.
- Joining: Result Unknown
Jamil has 6 candies. He buys 5 more. How many pieces of candy does Jamil have now?
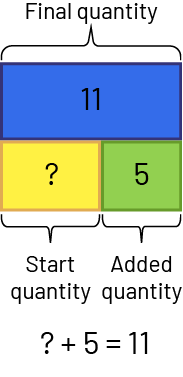
- Joining : Start Unknown
Jamil has some candy. He buys 5 more. He now has 11. How many candies did Jamil have initially?
- Joining : Change Unknown
Jamil has 6 candies. He buys a few more. He now has 11 pieces. How much candy did Jamil buy?
Separating Problems
The part-whole model can be useful for representing known and unknown values in separating problems. The set model is useful for representing the removal of a quantity.
- Separating: Result Unknown
Nadia has $150. She gives $50 to their brother. How many dollars does she have left?
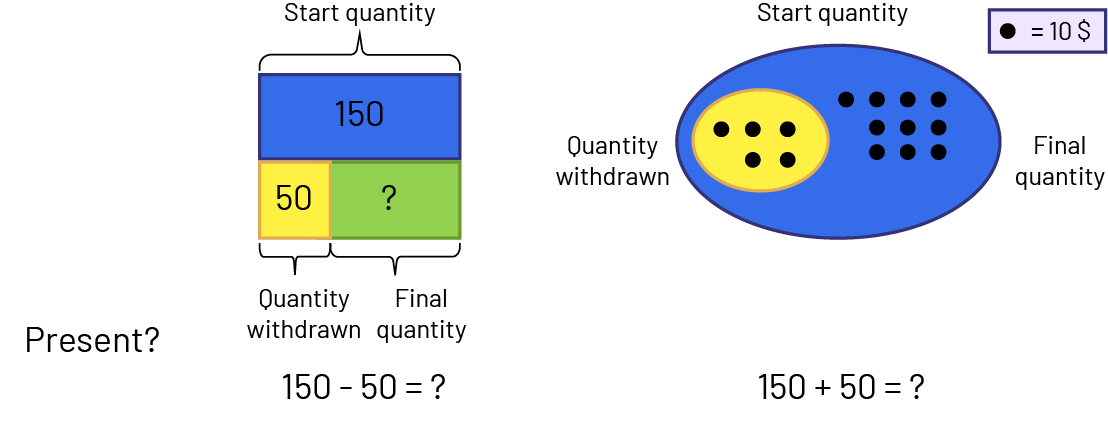
\(150 - 50 = \mathord{?}\)
- Separating: Result Unknown
Nadia has $150. She gives a few dollars to her brother. She now has $100 left. How many dollars did Nadia give to her brother?
- Separating: Start Unknown
Nadia had a certain number of dollars. She gave her brother $50. She now has $100 left. How many dollars did Nadia have initially?
Part-Part-Whole Problems
The part-whole model can be useful for representing known and unknown parts or the known and unknown whole in part-part-whole problems.
- Part-Part-Whole: Part Unknown
The class has a lot of crayons accumulated over the years. There are 800 crayons. 300 of these crayons are red. The remaining crayons are blue. How many blue crayons does the class have?
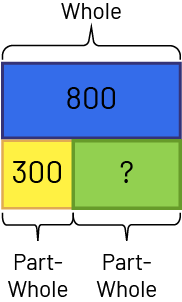
\(800 - 300 = \mathord{?}\)
- Part-Part-Whole: Whole Unknown
The class has a lot of crayons accumulated over the years. There are 300 red crayons and 500 blue crayons. How many crayons does the class have?
\(\mathord{?} - 300 = 500\)
Comparing Problems
The linear model can be useful for representing the difference between two numbers in comparing problems. In this example, we use the Cuisenaire rods and the double number line.
- Comparing: Difference Unknown
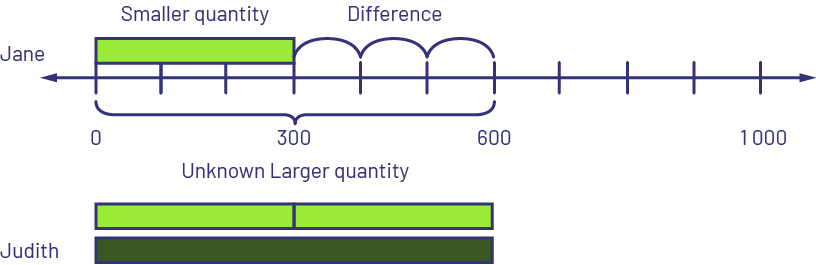
Judith has $600 and Jane has $300. How many more dollars does Judith have than Jane? OR Judith has $600 and Jane has $300. How much less does Jane have than Judith?
I know that the dark green rod represents 6 (hundreds), so I place it at the top of the number line from 0. I know that the lime green rod represents 3 (hundreds), so I place it below the number line from 0. I compare the 2 rods and see that the lime green rod is 3 (hundreds) less than the dark green rod. I find the difference or gap between the 2 quantities. There is a difference of $300. Judith has $300 more than Jeanne or Jeanne has $300 less than Judith.
- Comparing: Larger Quantity Unknown
Judith has $300 more than Jane. Jane has $300. How much money does Judith have? OR Jane has $300 less than Judith. Jane has $300. How much money does Judith have?
I know that the lime green rod represents 3 (hundreds), so I place it on top of the number line starting at 0. I take another lime green rod and place it below the number line starting at 0 and I add another lime green rod since Judith has $300 more than Jane. I replace the 2 lime green rods with the dark green rod which represents 6 (hundreds). Judith therefore has $600.
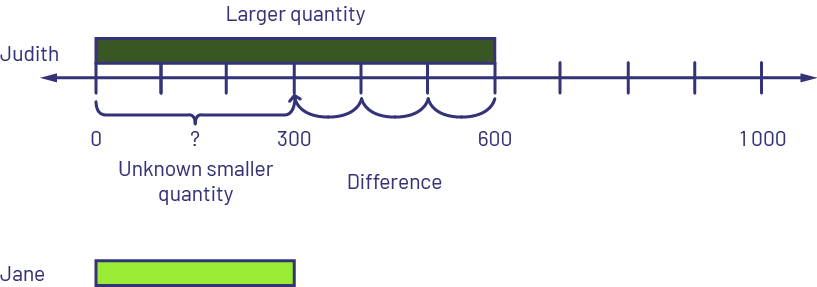
- Comparing: Smaller Quantity Unknown
Judith has $600 and Jane has $300 less than Judith. How much money does Jane have? OR Jane has $300 less than Judith. Judith has $600. How much money does Jane have?
I know the dark green rod represents 6 (hundreds), so I place it at the top of the number line starting at 0. On the number line, I count down 3 jumps to 300 to represent that Jane has 300 $ less than Judith. I take a lime green rod representing 3 (hundreds) and place it under the number line starting at 0. Jane has $300.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9-10.
Joining and separating problems are perceived by students as active situations, easier to model and "see" as the start quantity increases or decreases. Part-part-whole problems, however, assume a static situation, as no action or change occurs, making them more abstract and difficult to understand. Comparing problems, on the other hand, deal with the relationship between two quantities by opposing them: thus, there is no action, but a comparison of one quantity to another.
Since students are regularly exposed to problems whose final quantity is sought, they solve them more easily. However, they have more difficulty solving problems where the unknown is the initial quantity, the quantity joining, or the quantity being separated. These problems help develop a more solid understanding of the operations of addition and subtraction and the connections between the operations. For example, in the case of joining problems where the unknown is the initial quantity, students more easily see the advantages of addition (for example, \(?\; + \;12\; = \;37 \)) which makes it possible to respect the order in which the action takes place in the problem. This allows them to use a strategy (for example, counting up or down) to determine the initial quantity. These students demonstrate their understanding of the problem and their ability to use a strategy to solve it. However, they do not demonstrate an understanding of the meaning of difference (and subtraction). If they had used subtraction, that is \(37\; - \;12\; = \;?\), they would have demonstrated a broader understanding of the relationships between quantities in relation to this operation. However, a strategy should not be imposed on students while they are learning.
Requiring students to subtract will not help students who do not see the relevance of this strategy. However, if they are regularly exposed to a variety of problems and participate in the mathematical conversations that follow, they are able to see the connections between various strategies and to learn a variety of strategies. They then become more successful.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83-84.
Relationships Between Operations
The fundamental operations of addition, subtraction, multiplication and division are closely related despite their apparent differences. The more opportunities students have to work with the operations, the more they can notice and understand the relationships between them.
Addition and subtraction are inverse operations. However, when they are learning, students often have difficulty solving equations such as \(17 + \Delta = 31\). Many teachers encourage their students to use the inverse operation, namely subtraction. However, it may be learning a trick, unless students understand why subtraction is a possible strategy. They must first grasp the relationship of the whole and its parts as well as the meaning of a difference. For example, a number can be represented as follows:
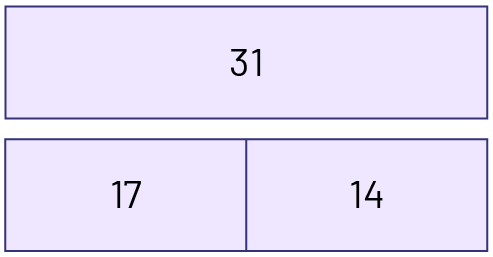
This way of representing the relationship between a number and its parts makes it possible to see that subtraction is the inverse operation of addition. Thus, since \(17 + 14 = 31\) and \(14 + 17 = 31\), therefore \(31 - 17 = 14\) and \(31 - 14 = 17\).
Additionally, students can see why addition is commutative \((14 + 17 = 17 + 14)\) and why subtraction is not \((31 - 17 \neq 17 - 31)\). Those who have acquired good number sense and are able to decompose and combine numbers can use their knowledge to more effectively solve equations such as \(17 + \rule{1cm}{0.15mm} = 31\ ) understanding that we are looking for the difference between 17 and 31.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 97-98.
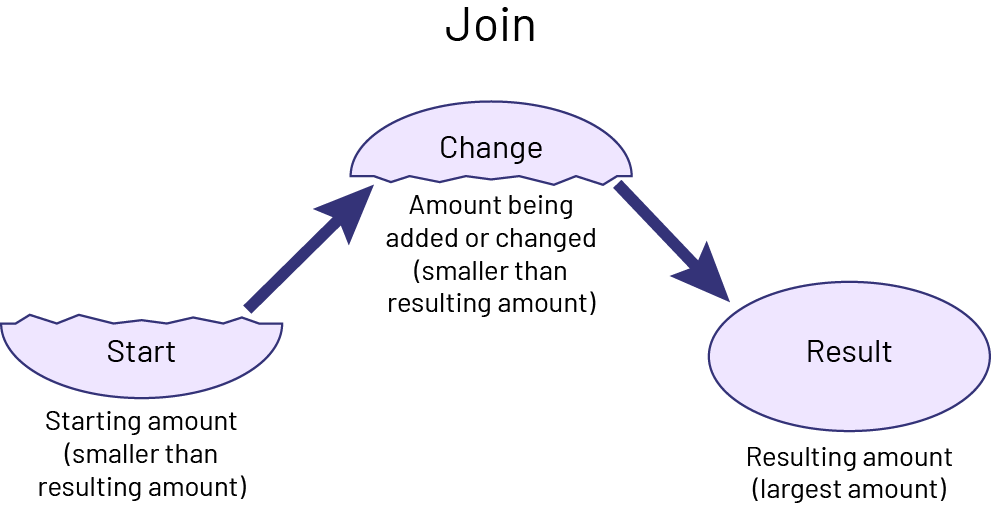
Knowledge: Joining Problem
In joining problems (with whole numbers), the result is the largest number.
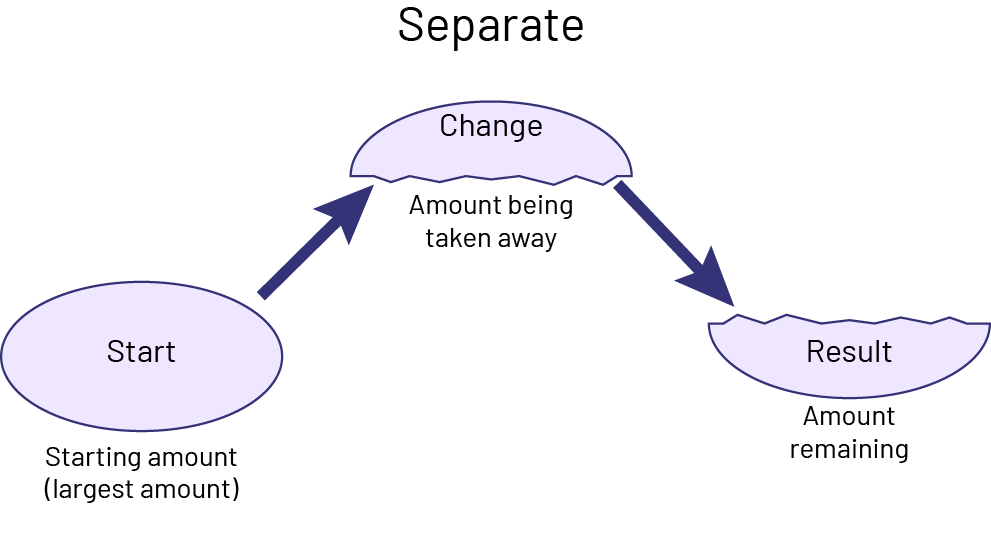
Knowledge: Seperating Problem
In separating problems with whole numbers, the first amount is the largest.
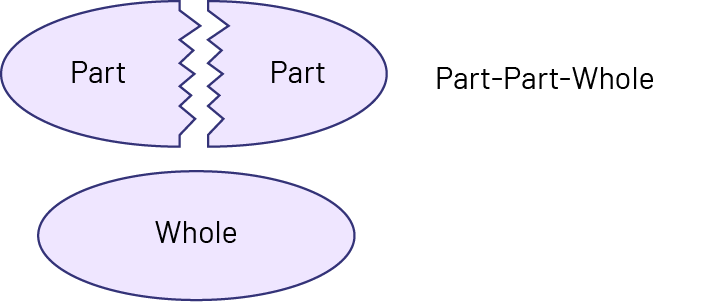
Knowledge: Part-Part-Whole Problem
Problems that focus on the part-part-whole relationship include two parts that are joined together as a whole.
Knowledge: Comparing Problem
In comparing problems, two quantities are compared. The third quantity is the difference.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 9-10.