B2.8 Represent the connection between the numerator of a fraction and the repeated addition of the unit fraction with the same denominator using various tools and drawings, and standard fractional notation.
Skill: Represent the Connection Between the Numerator of a Fraction and the Repeated Addition of the Unit Fraction With the Same Denominator
The word fraction comes from the Latin fractio which means "break". A part of a broken object can therefore represent a fraction, because it is a part of a whole. However, in order to determine a fraction of an object divided into parts, the parts must be equivalent. Note that when we talk about equivalent parts, we are not necessarily talking about identical shapes, although these are easier to use.
It is important for students to understand that the more the whole is divided, the smaller its parts.
In order to make understanding of fractions and equal partitioning more concrete, it is recommended that manipulative activities, such as folding and cutting, be introduced. These activities allow for a tactile examination of the quantity represented by a fraction. Indeed, splitting strips of paper to represent halves, thirds, fourths, and fifths of strips is an important exercise for students. Later, these strips can be used as models in other learning situations. These seemingly simple activities have amazing potential! Fractional strips are useful when counting in unit fractions.
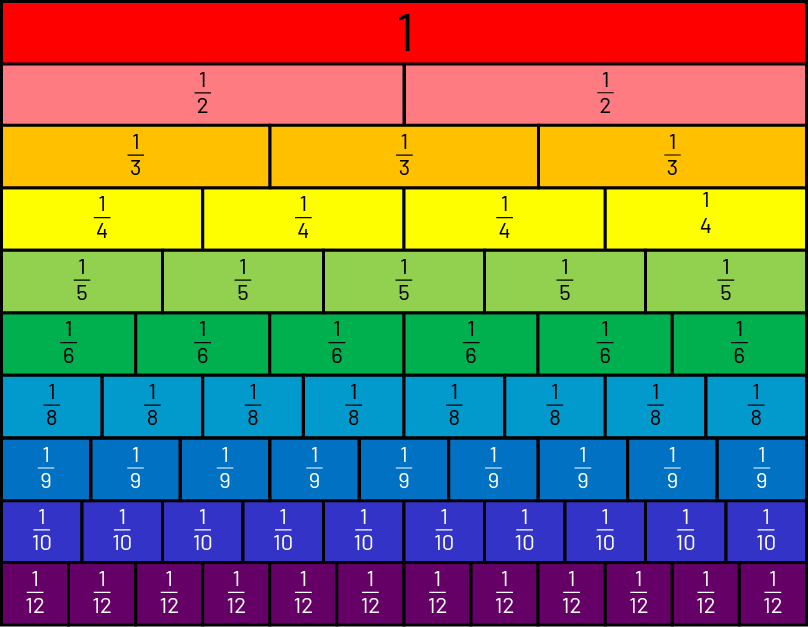
To count by a fractional amount is to count by a unit fraction. For example, when counting by the unit fraction one third, the sequence is: 1 one third, 2 one thirds, 3 one thirds, and so on. Activities that require counting by unit fractions can reinforce that the numerator is actually counting parts. A fractional count equivalent to the unit fraction makes one whole. For example, when a whole is divided into two equal parts, each part is called one half; when it is divided into three equal parts, each part is called one third; when it is divided into four equal parts, each part is called one fourth. When there are four or more equal parts, the suffix th is added to the number of parts to obtain fourths, fifths, twentieths, etc. A student who has mastered the concept of counting by a unit fraction does not need to recreate the image of the "pie" to understand, for example, that six sixths (\frac{6}{6}\) form a whole. Thus, in order to identify the fraction shown below, his reasoning might be, "I count the parts (1, 2, 3, 4, 5, and 6) and conclude that they are sixths. Since five (5) parts are shaded, I can state that 5 one sixths or five sixths (\(\frac{5}{6}\)) of the shape are shaded."
To demonstrate the relationship between the numerator of the fraction and the repeated addition of the unit fraction with the same denominator, students are asked to count the shaded parts of the whole into unit fractions. For example, the student would say "1 one-sixth," "2 one-sixth," "3 one-sixth," "4 one-sixth," "5 one-sixth.".
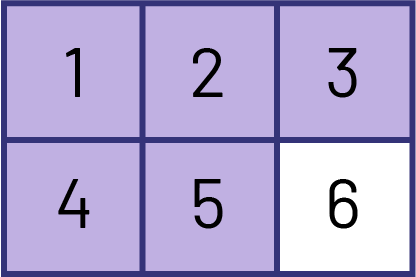
This process also leads them to recognize that a fraction can be the sum of unit fractions.
Example
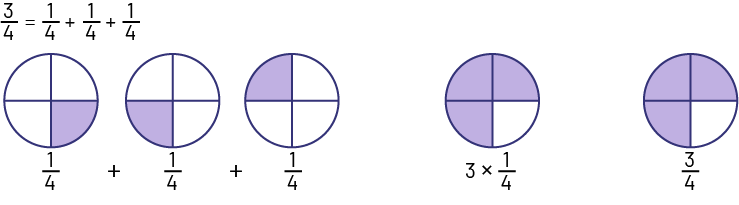
The student would count the "one-fourth": 1 one-fourth, 2 one-fourth, 3 one-fourth.
Subtraction is treated the same way. For example, if I subtract 3 eighths from 5 eighths, I have 2 eighths left. The student can count backwards in unit fractions:
"5 one eighth", "4 one eighth", "3 one eighth", "2 one eighth".
Students who have counted, for example, equivalent parts of wholes can explain that the denominator represents what is being counted (for example, fourths) and the numerator represents how many parts there are.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 33-35.
Knowledge: Unit Fraction
Fraction whose numerator is one (1) (for example, \(\frac{1}{3} \), \(\frac{1}{9} \)).
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 35.
Knowledge: Numerator
Number of equal parts of the whole being considered.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Knowledge: Denominator
Number of equal parts by which the whole is divided.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.